基于近场动力学的隧道衬砌结构渐进裂损数值模拟分析

2019-05-27马云峰徐林生

西安理工大学学报 2019年1期

马云峰，徐林生

(1.重庆交通大学土木工程学院，重庆400074；2.重庆水利电力职业技术学院市政工程系，重庆402160)

截止到2016年年底我国公路隧道共计15 181处、总长度14 037.9 km，其中特长隧道共计815处、总长度3 622.7 km，长隧道共计3 520处、总长度6 045.5 km[1]。伴随着隧道建设事业的磅礴发展，运营隧道的病害问题日益突出，尤其是衬砌裂损给隧道的安全运营带来巨大隐患。隧道衬砌裂损的实质主要是由于作用于隧道结构的荷载超出其承载能力产生的，但最终都会反映在隧道的二衬结构上。近几年国内外诸多学者对隧道衬砌病害的探索研究取得了一系列的研究成效[2]。但是对于衬砌裂缝的大多数研究还是依托工程实例，尚未能对裂缝的开裂机理、裂纹的动态扩展、裂缝的影响因素和分布规律形成完整系统的认识[3]。尽管目前数值分析对衬砌裂缝的研究取得了较大的进展，但大部分还是针对衬砌裂缝部位及裂损部位的应力和变形研究展开的，而且在模拟精度上参数的选取和模型精确性还需进一步研究[4]。有限单元法(FEM)由传统连续介质力学发展而来，对于求解断裂损伤问题需要预判开裂位置及扩展方向，而且对于网格的依赖性较强，计算过程较为复杂，计算结果往往与实际情况差异性较大。近场动力学理论(PD)在求解非连续性问题时基于非局部作用的积分思想，避免了由于微分方程求解而产生的奇异性问题，但其求解的计算效率远低于有限单元法[5]。近场动力学和传统有限元混合建模的方法在分析衬砌损伤和开裂方面能够有效提高计算精度和计算效率，加快收敛速度。将计算模型中的FEM域和PD域根据应变能密度等效原则进行耦合。在验证模型的可行性基础上对衬砌裂缝的扩展和分布规律进行分析探讨。

1 近场动力学与有限元混合模型

1.1 ABAQUS计算模型离散化

将模型的PD域离散为具有密度和体积信息的物质点，得到控制方程在时间和空间上的离散化形式[6]：

(1)

式中：ρ为物质点的物理密度；xi和xj为近场范围内任两物质点的位置；ui和uj为两物质点的位移；n为时间步长；Vj为j处物质点体积；bi为物质点外荷载的密度；f为本构力函数。

1.2 本构关系和破坏准则

本构模型采用修正的PMB模型，物质点对视为cohesive单元(键)连接。当‖ξ‖δ时，物质点对相互作用的本构力函数f表示形式为[7]：

(2)

当‖ξ‖>δ时，f=0。式中：ξ为物质点对相对位置；δ为近场范围；η为物质点对的相对位移；E为弹性模量；c为材料的微模量；μ为物质点产生的位移；s为物质点对的相对伸长率。

PD理论中对于损伤断裂的描述引入了标量函数σ和φ(x,t)来表示[8]：

(3)

式中，s0为物质点对的临界伸长率。当μ=0时，表示物质点对之间的相互作用消失，微观的键断裂映射在宏观上产生了裂纹，当物质点的破坏累积成面时，就形成了宏观的断裂，该点近场范围内裂损度用φ(x,t)表示[9]：

(4)

式中，H为空间域内物质点x的进场范围。

近场动力学应变能密度的表达式为[10]：

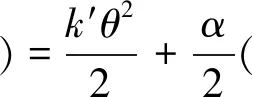
(5)

式中：α、k′ 为待求参数；ω为影响函数；θ为体积膨胀率；ed为伸长状态的偏张量；W为应变能密度。

由传统应变能密度和近场动力学应变能密度相等可以推出：

(6)

式中：k、G分别为体积模量和剪切模量；m为加权体积标量。

为了模拟隧道衬砌开裂状态建立基于能量的损伤耦合方程[11]：

Ψ(e,φ)=W[(1-φ)e]

(7)

由式(1),(4)～(7)可得：

(8)

式中：M为沿着变形键方向的单位矢量。

2 衬砌裂缝近场动力学可行性研究

日本隧道研究中心曾于2000年开展过1:1衬砌模型室内试验，在衬砌外表面周身布设千斤顶来模拟围岩抗力和外加荷载，主要针对衬砌拱顶集中荷载和拱顶30°范围的衬砌背后空洞等工况作用下衬砌的开裂情况进行研究。具体参数详见文献[12]。为了验证近场动力学模拟衬砌裂缝开裂过程，选取30°范围的衬砌背后空洞工况进行对比分析。为了贴合原型试验，本文的数值模拟不考虑隧道仰拱的作用，同时忽略隧道埋深对其衬砌结构开裂的影响，选取0°～180°范围内衬砌进行研究(见图1)。

图1 隧道模型示意图Fig.1 Sketch of tunnel model

分析过程中主要考虑了三种破坏模式，一种是由于混凝土达到极限压应变而产生的压溃；一种是由于混凝土达到极限拉应变而产生的拉裂；一种是由于裂缝的延展而导致的隧道衬砌承载力失效。基于应变能密度等效的原则，裂缝的扩展准则采用应变能密度因子准则。衬砌的损伤采取最大应力准则，损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化准则。

图2～3分别是近场动力学方法和室内原型试验得到的荷载-拱顶位移对比曲线和裂缝分布状态对比图。对比结果显示，二者在荷载-拱顶位移曲线中趋势相同，曲线拟合较好，数值模拟前期加载产生的拱顶位移大于原型试验；数值模拟后期加载产生的拱顶位移小于原型试验。对原型试验过程分析，千斤顶模拟外加荷载和围岩抗力的不均匀性是造成结果差异的主要原因。裂缝分布状态图中显示二者在开裂位置和裂缝分布上的结果基本吻合。因此，采用近场动力学方法来模拟衬砌裂缝渐进裂损过程是可行的。

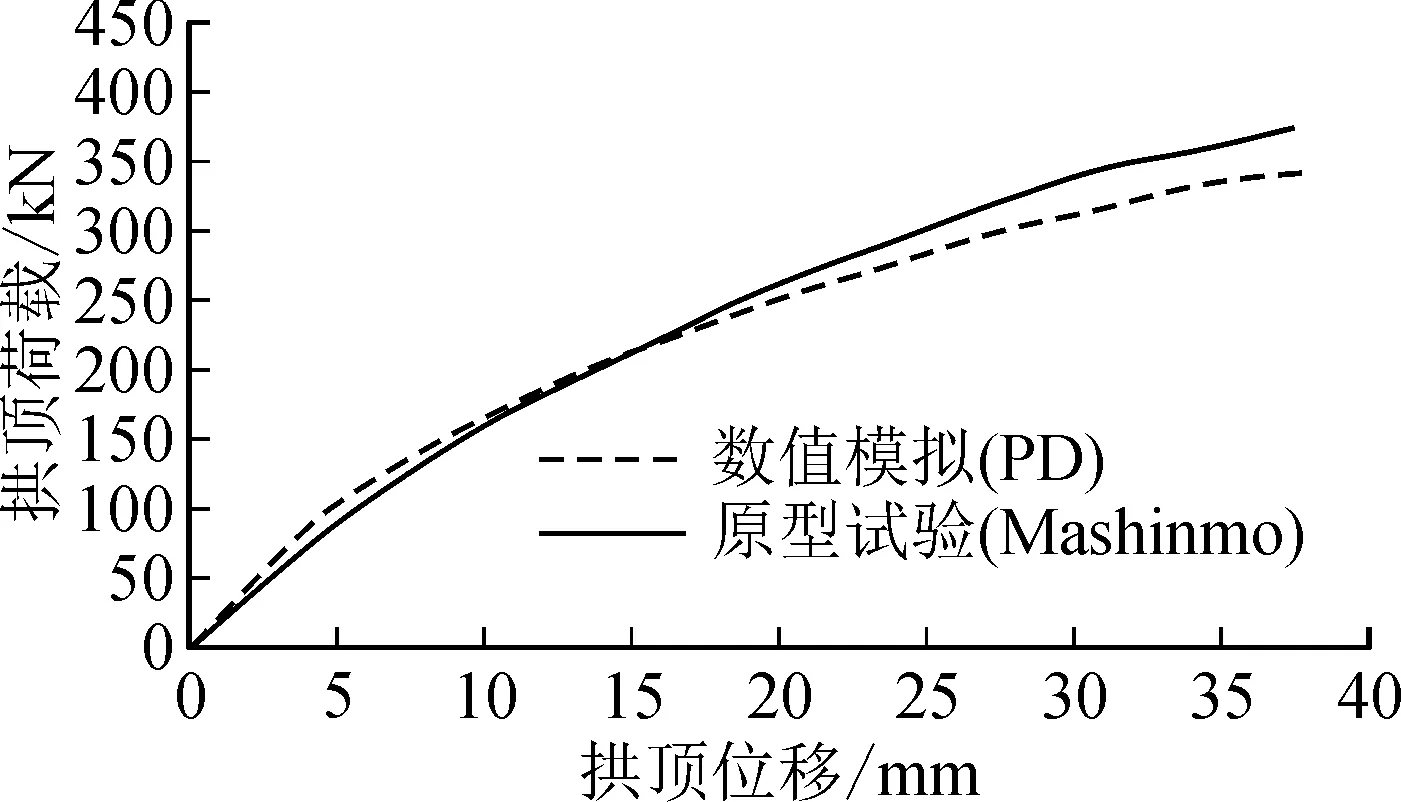
图2 数值模拟与原型试验荷载-拱顶位移对比曲线Fig.2 Comparing load-vault displacement curves between numerical simulation and prototype test

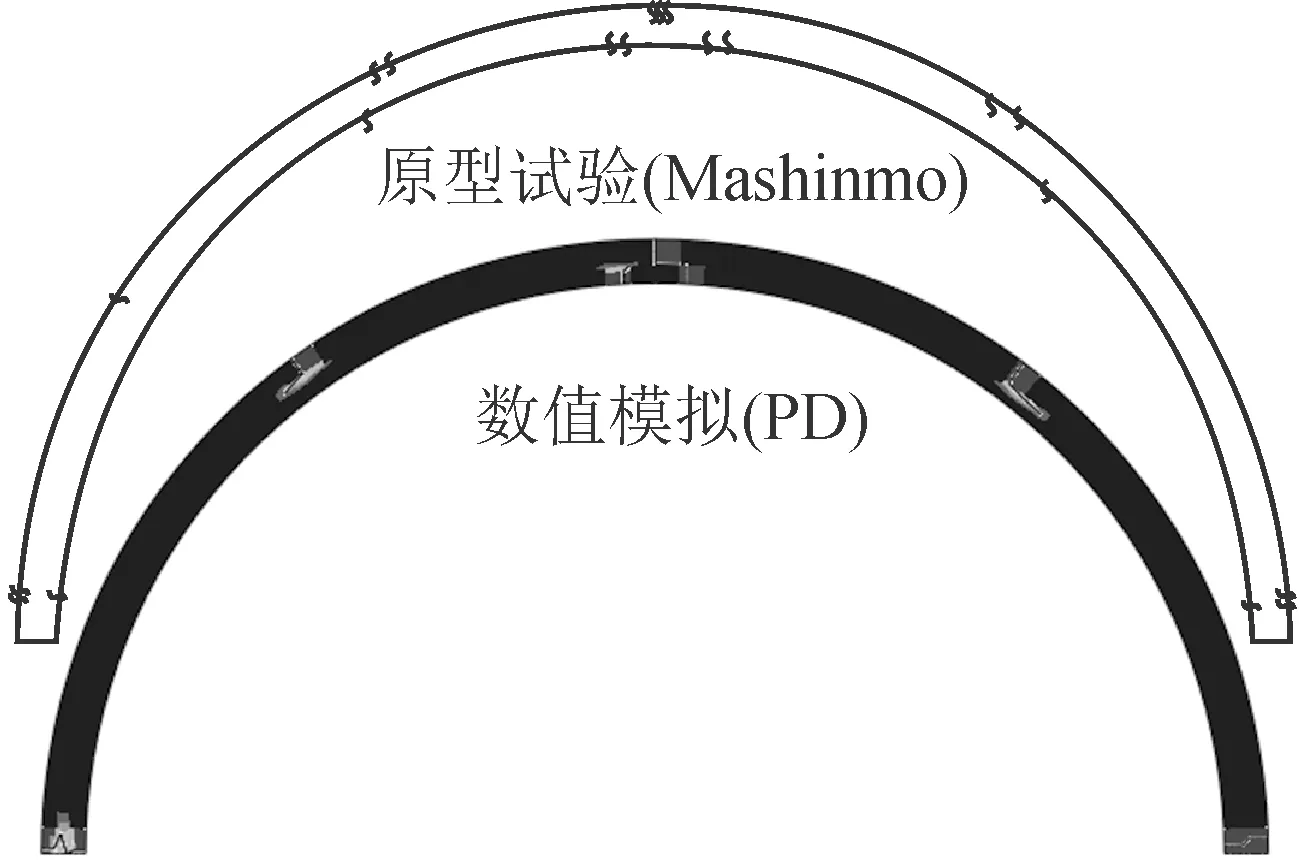
图3 数值分析与原型试验裂缝分布状态对比图Fig.3 Comparison of fracture distribution between numerical analysis and prototype test

3 隧道衬砌渐进裂损近场动力学分析

本文主要以天水市八盘山隧道的维护完善工程为主要实例，进行衬砌结构渐进裂损的数值模拟。模型相关参数：隧道半径为5 250 mm，衬砌厚度为55 cm厚C20混凝土，断裂能为G1C=G2C=G3C=60 N/m，Young模量为21 GPa，Poisson比为0.3，围岩压力为22 kPa，采用弹簧单元模拟围岩抗力。利用ABAQUS中的镶嵌单元技术模块实现有限元域和近场动力学域的混合建模，将隧道衬砌开裂部位划分为FEM域和PD域，见图4。根据式(2)cohesive单元的刚度为：

(9)

图4 FEM节点和PD物质点连接示意图Fig.4 Diagram for connection between FEM node and PD material point

选取对我们所关心的裂缝扩展区域采用四结点二维cohesive单元，其他区域采用四结点双线性平面应变四边形单元，并对开裂区域网格加密。

3.1 局部偏压

偏压现象主要是由于荷载的不对称性产生的，本文不考虑地形的不对称产生的偏压，仅分析荷载局部偏压对隧道衬砌开裂的影响，计算模型见图5。以隧道左侧80°为荷载偏压基线，选取10°(80°～70°)、20°(80°～60°)、30°(80°～50°)、40°(80°～40°)四种局部单偏压工况进行分析研究。

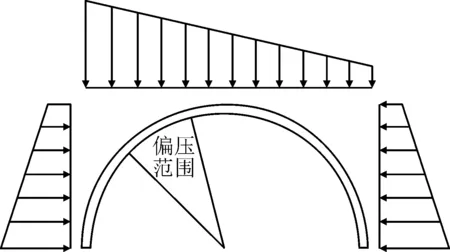
图5 偏压计算模型图示Fig.5 Graphics of bias pressure computing model

图6反映了裂缝的扩展状态，给出衬砌四种工况下裂纹水平层次集的等值面。随着偏压荷载的不断增大，在衬砌内表面偏压荷载的中心附近出现一条剪拉状态的主裂缝，并伴随荷载的增加主裂缝继续扩展由剪拉状态转变为剪压状态，其两侧出现新裂缝的发育并呈现剪压状。从初始围岩压力作用到衬砌承载力失效的过程中，外表面的混凝土首先被压溃，内表面混凝土由张裂转变为压溃，最终随着裂缝贯通导致衬砌结构失效。

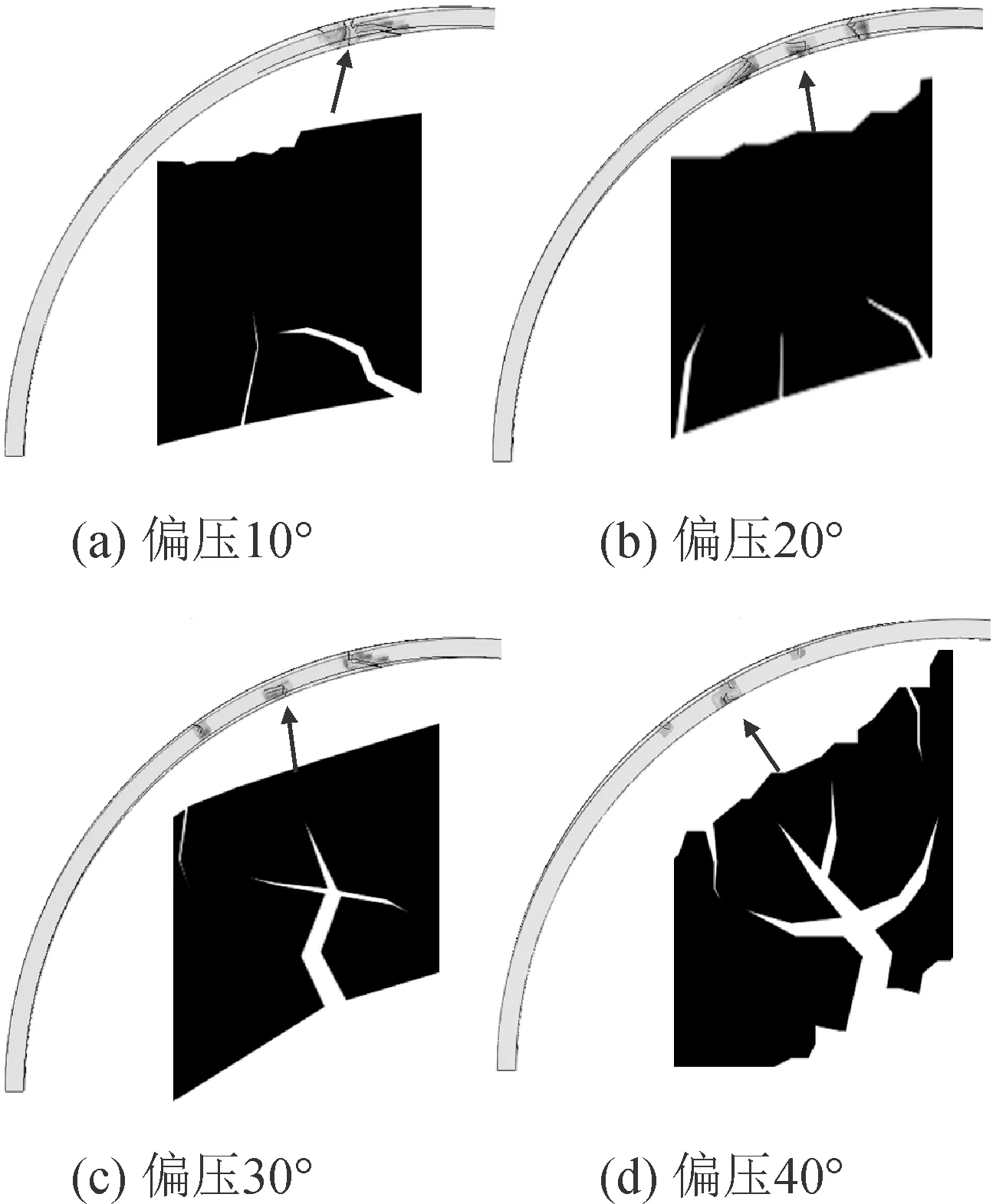
图6 偏压作用裂缝分布状态图Fig.6 Fracture distribution state diagram under bias pressure

伴随着衬砌裂缝的扩展，在偏压范围内出现不同程度的位移，根据内表面主裂缝的扩展状态，以裂缝的径向深度来分析位移和裂缝扩展的关系见图7。

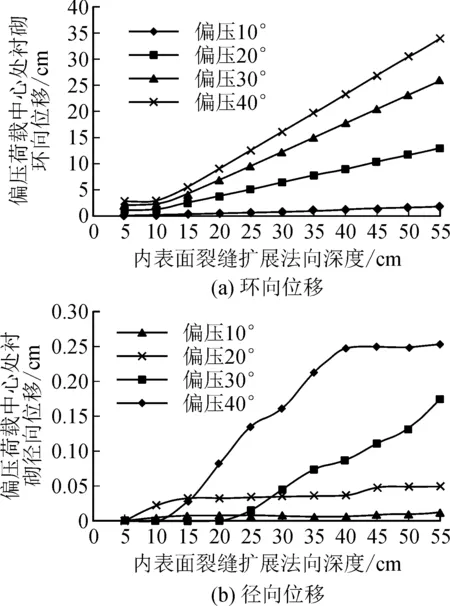
图7 偏压作用主裂缝扩展法向深度与位移关系图Fig.7 Relation diagram of normal depth and displacement of main crack propagation under bias pressure

伴随着裂缝深度的不断增加产生的环向位移和径向位移也逐渐增大。随着偏压范围的增加，衬砌的位移随裂缝深度扩展变化明显，直到裂缝贯穿衬砌，位移的变化没有平缓的过程，可见衬砌的破坏主要是由于裂缝扩展而导致的衬砌承载力失效。

图8给出了衬砌内表面主裂缝尖端单元应变能和时间历程关系图。随着偏压范围增加，裂缝尖端的应变能也随之减小，说明衬砌承载力失效所需的破坏荷载随偏压范围增加而减小。在加荷的中前期裂缝主要经历成核状态并呈现稳态扩展，随荷载的逐步增加裂缝由剪拉状态向剪压状态转变，应变能呈现减少趋势，而后出现失稳扩展状态，最终达到断裂。

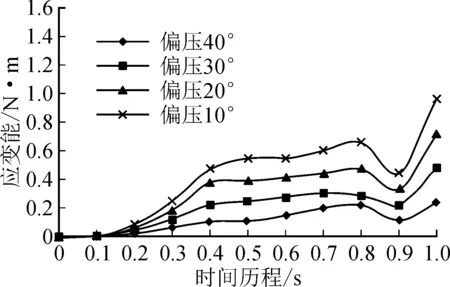
图8 偏压作用主裂缝应变能时程关系曲线Fig.8 Strain energy time-history curve of main crack under bias pressure

3.2 背后空洞

本文采用弹簧单元的失效来模拟衬砌背后空洞(见图9)，初始状态围岩压力均匀分布于衬砌周身，每一个分析步开始移除空洞范围衬砌围压作用，重新分布围岩压力，将空洞围压在每一个分析步中按时间增量均匀加载在其他衬砌上。逐渐增加围岩压力直至裂缝扩展导致衬砌承载力失效。在此过程不考虑拱腰范围空洞大小，主要分析拱顶10°、20°、30°、45°对称范围空洞大小(4种工况)对衬砌开裂的影响。

图9 背后空洞计算模型图示Fig.9 Diagram of calculation model for back cavity

图10给出了衬砌四种工况下裂纹水平层次集的等值面。随着围压的增加，拱顶10°、20°工况下，拱肩和拱脚出现了较为明显的裂缝扩展，拱肩外表面出现主裂缝有向拱顶延展趋势并最终贯穿衬砌，拱顶20°工况下，拱顶开始出现明显裂缝扩展；到拱顶30°、45°工况时衬砌周身均出现了明显的裂缝扩展，裂缝的增扩现象较为明显，其中在拱腰外表面出现了主裂缝贯穿衬砌。在此过程中空洞范围的边界附近最先出现裂缝的扩展，裂缝多呈剪拉状态，拱脚位置的裂缝主要呈剪压状态。拱顶10°、20°工况下拱脚外表面混凝土首先压溃，随着空洞范围的不断增大，拱顶内表面混凝土也出现压溃，最终随着裂缝的贯通，整个衬砌承载力失效。

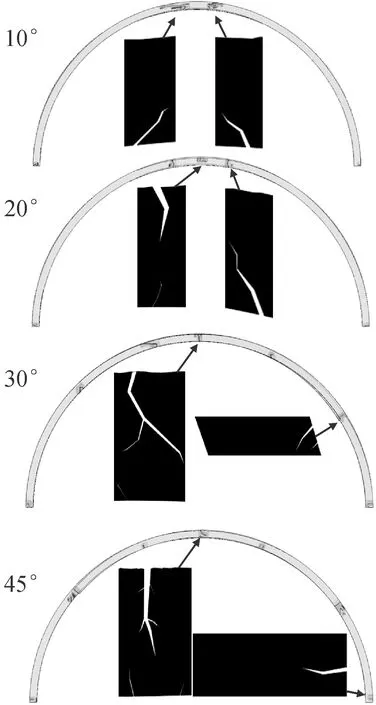
图10 背后空洞裂缝分布状态图Fig.10 State graph of fracture distribution in back cavity

在加载破坏的过程中，空洞 20°工况时拱顶外表面出现较为明显的裂缝扩展，随着空洞范围增大，裂缝由剪拉状态向剪压状态转变，并产生不同程度位移，按照时间增量分析拱顶内表面位移发展关系，见图11。

图11 背后空洞作用下主裂缝扩展法向深度与位移关系Fig.11 Normal depth and displacement of main crack propagation under back cavity

初期加载过程位移曲线出现了明显上扬，主要是材料的接触变形和自压缩产生的形变，随着荷载的持续增加，在加载过程的中后期拱顶内表面的混凝土出现较为明显的压溃，位移也出现了小幅度的回落。整个时间历程中，环向位移明显大于径向位移，随着空洞范围增大，产生的位移量也逐步增加。

以贯穿衬砌的主裂缝来分析在整个时间历程中应变能的变化规律见图12。不同拱顶空洞范围的应变能随时程的发展呈现逐级增大趋势，可见裂缝的扩展过程没有出现受力状态的转变。空洞范围较大的工况下衬砌裂缝产生应变能较大，裂缝扩展速率也较大。

图12 背后空洞作用下主裂缝应变能时程关系曲线Fig.12 Time-history curve of strain energy of main crack under back cavity

3.3 衬砌厚度不足

本文以八盘山隧道衬砌厚度55 cm为基本模型，衬砌厚度30 cm为衬砌厚度不足模型，隧道的外径不变，分析从初始围压加载至30 cm厚度衬砌发生裂缝的延展而导致的衬砌承载力失效时整个过程衬砌裂缝开裂状态和分布规律，计算模型见图13。

图13 衬砌厚度不足计算模型图示Fig.13 Diagram of calculation model for insufficient lining thickness

图14为30 cm和55 cm两种厚度衬砌模型破坏时衬砌裂缝的分布状态图。在持续加载的过程中，两种结构开裂部位较为相似，30 cm厚度衬砌模型发生破坏时，裂缝多以张开型裂缝为主，拱顶部位产生贯穿裂缝，55 cm厚度衬砌模型在拱腰部位产生最大长度裂缝为8 cm，裂缝宽度0.25 cm。

图15为两种模型中最大裂缝的扩展深度随时间历程的关系曲线。当最大裂缝扩展至相同长度，30 cm厚度衬砌需要荷载较小。从两条曲线斜率的发展趋势可以看出，30 cm厚度衬砌裂缝的扩展速率远大于55 cm厚度衬砌。

图14 不同的衬砌厚度裂缝分布状态图Fig.14 State diagram of crack distribution in different lining thicknesses

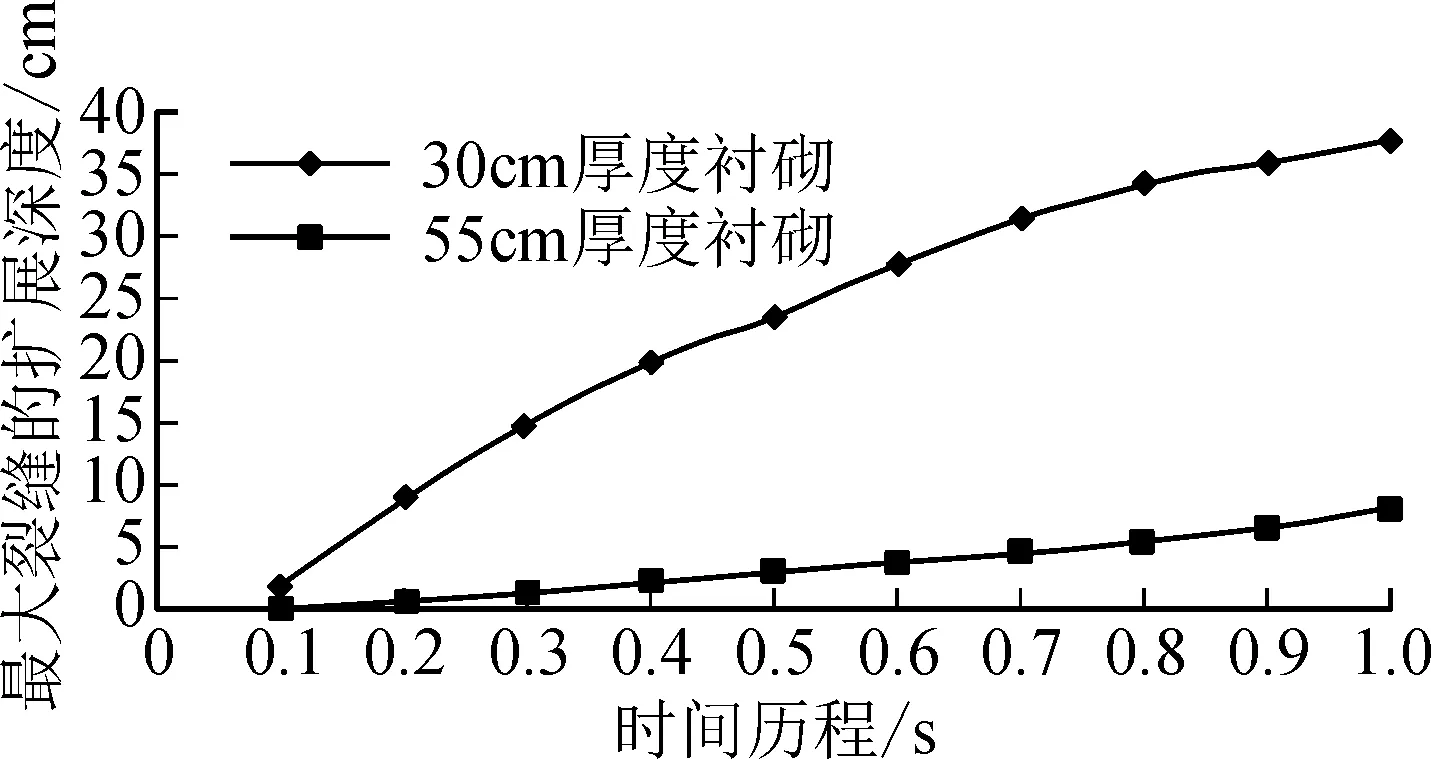
图15 最大裂缝扩展深度的时程曲线Fig.15 Time-history curve of maximum fracture propagation depth

为了更好反应衬砌厚度不足情况下衬砌的渐进裂损状态，输出整个模型应变能随时间历程的变化，见图16。55 cm厚度衬砌在整个加荷过程中应变能变化较为平缓，裂纹扩展基本处于稳态扩展阶段。30 cm厚度衬砌在加荷中期后期，曲线出现断层式跳跃并以更大的斜率不断增长，说明在此阶段裂缝已经进入失稳扩展状态，并且裂缝在衬砌周身大面积扩展，直至裂缝的扩展而导致衬砌承载能力失效。