随从力作用下薄膜的非线性自由振动特性研究
2019-05-27邵明月武吉梅应戍狄
邵明月,武吉梅,,应戍狄,王 砚,卢 瑶
(1.西安理工大学 机械与精密仪器工程学院,陕西西安710048; 2.西安理工大学 印刷包装与数字媒体学院, 陕西 西安 710048; 3.西安理工大学 土木建筑工程学院, 陕西 西安 710048)
作用于系统的非保守力随结构的变形而变化,一般称其为随从力(follower force)或伴生力[1],其作用机理与分布阻力有一定的相似性。非保守系统的动力学分析在工程中有着广泛的应用,如运动的薄膜、飞行器等受到的空气阻力都属于非保守力。在印刷过程中,受到空气阻力的影响,薄膜的振动会出现更为复杂的动态特性,从而严重影响印刷品的套印精度。本文以运动薄膜为研究对象,将空气阻力模化为随从力,对随从力作用下的薄膜的非线性动力学特性及其稳定性进行研究,为印刷机的设计、制造以及印刷机的稳定性提供理论指导和依据。
对于随从力作用下的系统运动稳定性研究,国内外学者已经做了大量的工作。Higuchi 和Dowell[2]研究了受到切向随从力的柔性矩形板的动态稳定性,结果表明阻尼和板的长宽比对稳定性有很大影响。Choo 和Kim[3]采用多尺度法研究了四个自由边受脉冲随从力作用下的各向同性和非对称层合板的动力稳定性。Alidoost 和Rezaeepazhand[4]研究了受集中随从力作用下的分层组合梁的振动、屈曲和颤振不稳定性问题。Robinson 和Adali[5,6]应用微分求积法研究了切向均匀分布力和三角分布切向随从力下粘弹性矩形板的动力稳定性问题。Lad 和 Kartik[7]研究了随从力作用下轴向运动弦线的横向振动特性,分析了随从力和粘性耗散对系统特征结构的影响。Karimi-nobandegani等[8]应用有限元法研究了裂纹对分布随从力作用下旋转非均匀梁的颤振不稳定性的影响。李清禄等[9]研究了由陶瓷和金属两种材料组成的功能梯度材料(FGM)圆板在非保守随从力作用下的稳定性问题。Wang等[10]应用无网格Galerkin方法研究了随从力作用的粘弹性压电层合板的稳定性。Guo等[11]采用微分求积法研究了均匀分布的切向随从力作用下热弹性耦合矩形板的动力特性和稳定性。
近年来,已有人对运动矩形纸带非线性振动特性及稳定性进行研究。Marynowski[12]将运动薄膜简化成梁模型,并采用Galerkin 法和4阶龙格库塔法研究了二维轴向运动薄膜的非线性振动特性。Soares 和Gonçalves[13]应用有限元法研究了拉伸超弹性薄膜的非线性振动和稳定性问题。Liu等[14]采用数值分析法研究了预应力矩形正交各向异性薄膜结构在冲击载荷作用下的非线性振动响应。王砚等[15]采用微分求积法研究了非均匀张力作用下薄膜的张力变化系数、长宽比和运动速度对薄膜动力特性及稳定性的影响。Li等[16]研究了冲击载荷下的各向异性薄膜结构的非线性振动响应,并进行了可靠性分析。
综上,鲜见对随从力作用下运动薄膜非线性振动的研究。本文以印刷运动薄膜为研究对象,研究随从力作用下的薄膜的非线性振动特性。基于Von Karman薄板理论建立薄膜的横向振动方程,应用Galerkin方法对振动偏微分方程组进行离散,利用数值法分析随从力和无量纲速度对薄膜非线性振动特性的影响。
1 纸带的非线性振动方程
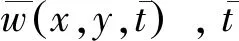

图1 随从力下运动纸带力学模型Fig.1 The mechanical model for the axially moving web subjected to follower force
平衡微分方程为:
(1)
其中Nx、Ny、Nxy、Nyx是薄膜单位长度所受的张力值。
弹性曲面微分方程为:
(2)
式中,φ为内力函数。
由中面内力及挠度所表示的系统相容方程:
(3)
式中,μ为泊松比;E为弹性模量;h为薄膜厚度。
薄膜力用内力函数φ可表示成:
(4)
由于薄膜单元的各个平衡微分方程相互之间是独立的,所以可认为:
(5)
根据Von Karman大挠度薄板理论[18]得到随从力作用下运动薄膜的非线性振动方程组为:
(6)
对式(6)引入下列无量纲量:
(7)
则式(6)可化为无量纲形式:
(8)
对于上述大挠度振动的基本方程,其边界条件为:
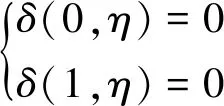
(9)
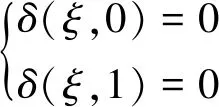
(10)
2 系统状态方程
采用分离变量法和Galerkin法对式(8)进行离散,令:
w(ξ,η,t)=W(ξ,η)q(t)
(11)
f(ξ,η,t)=F(ξ,η)q2(t)
(12)
式中,q(t)为时间变量。
取满足边界条件的位移函数为:
W(ξ,η)=sinπξsinπη
(13)
将式(13)代入式(8)中,得到
(14)
求解式(14),得出:
(15)
由Galerkin法得:
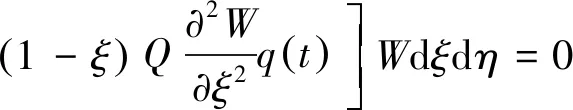
(16)
因此运动薄膜非线性振动的系统状态方程为:
(17)
其中
(18)
则有:
(19)
其中:

(20)
3 数值法求解
对式(19)首次积分得:
(21)
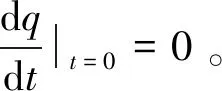
令:

(22)
可以得:
(23)

(24)
其中Z(n)为第一类完全椭圆积分,由此可得随从力下运动薄膜非线性振动的频率为:
(25)
其中:

(26)
可得:
(27)
其中:

(28)
4 结果及分析
4.1 非线性振动频率与随从力的关系
图2为初始运动条件L=1和无量纲速度c=0.5,长宽比r分别取0.5、1、2时,轴向运动薄膜非线性振动复频率ω与随从力Q之间的变化曲线。
令薄膜的长宽比r不变,由图2可知:当随从力Q=0时,无量纲复频率ω是一个实数;随着随从力Q的逐渐增大,复频率ω的实部逐渐减小,而虚部始终为零,说明运动薄膜进行的大挠度振动很小;当随从力Q继续增大到0.13,且长宽比r=0.5时,模态频率ω的实部减小至零,当随从力为0.195时,虚部开始由零逐渐增大,此时薄膜开始发散失稳。
因此,比较不同长宽比r的运动薄膜,可以明显看出,长宽比r越小,随从力Q越大时,薄膜越容易产生振动发散失稳现象。
图3为初始运动条件L=0和无量纲速度c=0.5,长宽比r分别取0.5、1、2时,轴向运动薄膜非线性振动复频率ω的实部和虚部与随从力Q之间的变化曲线。
由图3可知:随着随从力的逐渐增大,薄膜非线性振动的无量纲复频率ω实部始终为零(即频率ω为纯虚数),而虚部始终为定值。由此说明薄膜始终是发散失稳的,随从力的变化不影响系统发散失稳的快慢,且该现象与薄膜的长宽比无关。
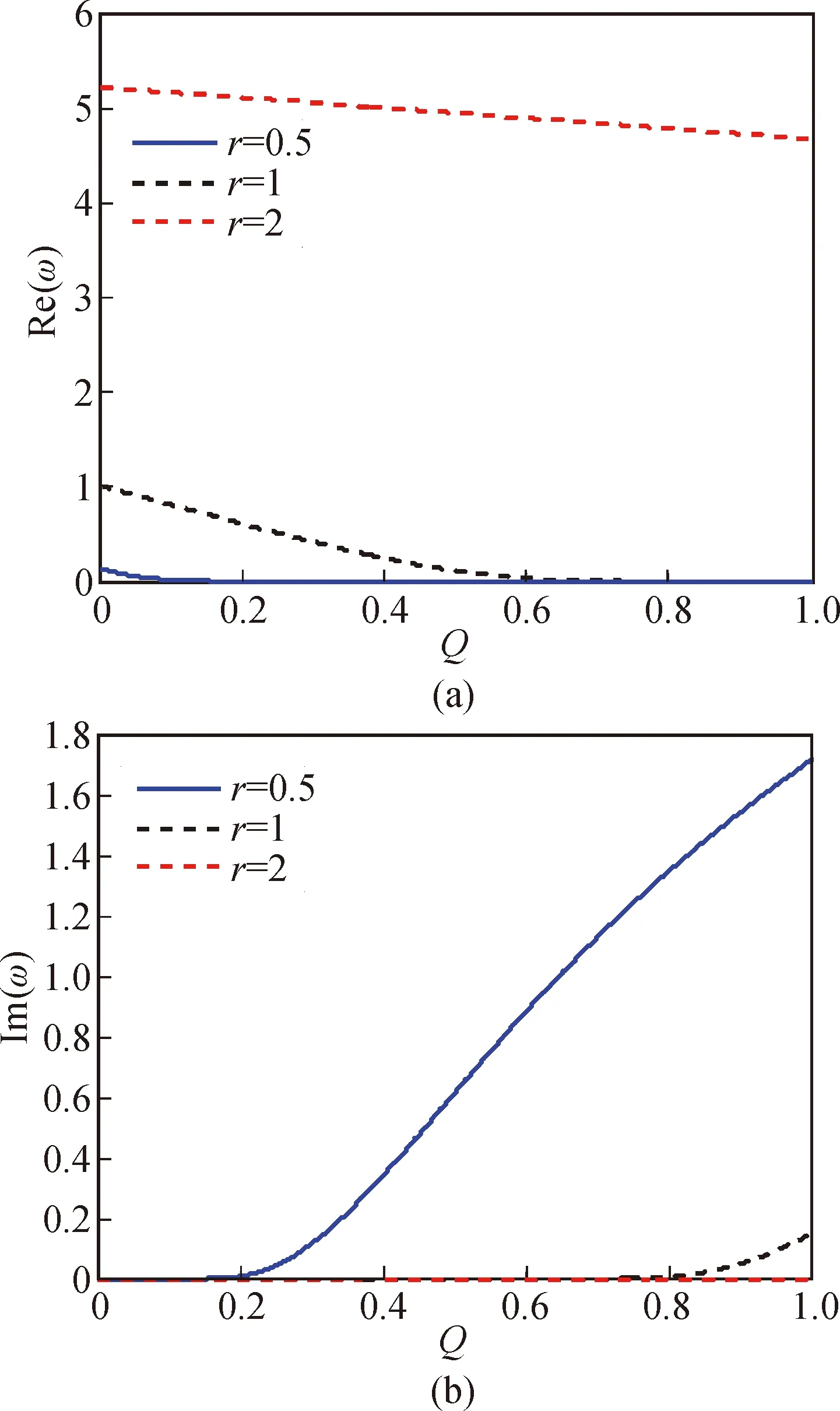
图2 L=1时无量纲非线性振动复频率ω与随从力Q的变化曲线Fig.2 The relationship between dimensionless complex frequency and follower force when L=1
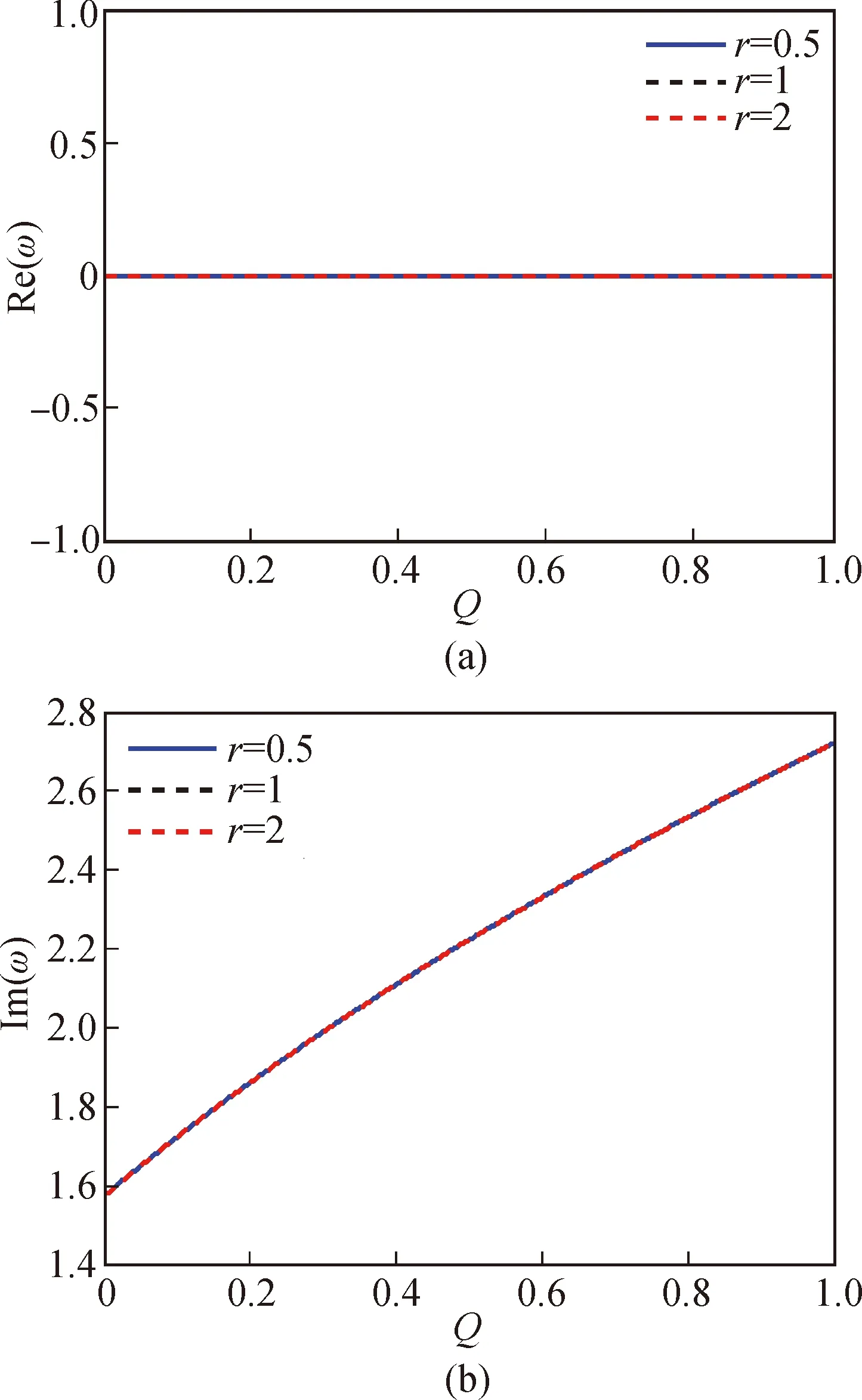
图3 L=0时无量纲复频率ω与随从力Q的变化曲线Fig.3 The relationship between dimensionless complex frequency and follower force when L=0
4.2 非线性振动频率与速度的关系
图4为初始运动条件L=1和长宽比r=1,随从力Q分别取0、0.5、1时,轴向运动薄膜非线性振动复频率ω随运动速度变化的关系曲线。
令薄膜的随从力Q不变,由图4可知:当无量纲速度c=0时,无量纲复频率ω是一个实数;随着无量纲速度c的逐渐增大,复频率ω的实部逐渐减小,而虚部始终为零,说明运动薄膜进行的大挠度振动很小;若速度c继续增大到某个值时,模态频率ω的实部减小至零,而虚部开始由零逐渐增大,此时薄膜开始发散失稳。
因此,比较不同随从力Q的运动薄膜,可以明显看出,随从力Q越小,薄膜振动失稳的临界速度越大,也就是说,减小薄膜的随从力Q可提高薄膜振动失稳的临界速度,使失稳的临界速度高于薄膜的工作速度,能够有效地保证薄膜工作在稳定的状态。
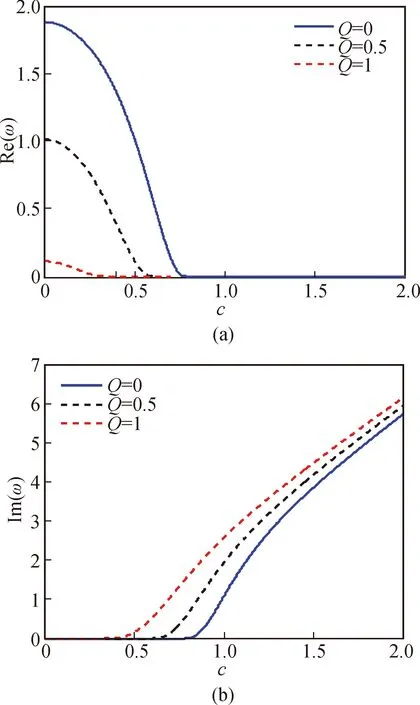
图4 L=1时无量纲复频率ω与无量纲速度c的变化曲线Fig.4 The relationship between dimensionless complex frequency and dimensionless velocity when L=1
图5给出的是初始运动条件L=0,长宽比r=1,随从力Q分别取0、0.5、1时,轴向运动薄膜非线性振动复频率ω的实部和虚部随运动速度变化的关系曲线。由图5可知:随着运动薄膜无量纲速度的逐渐增大,薄膜非线性振动的无量纲复频率ω实部始终为零(即频率ω为纯虚数),而虚部由零开始增大。由此说明薄膜始终处于发散失稳的状态,速度越大,发散失稳越快,且该现象与薄膜的随从力无关。
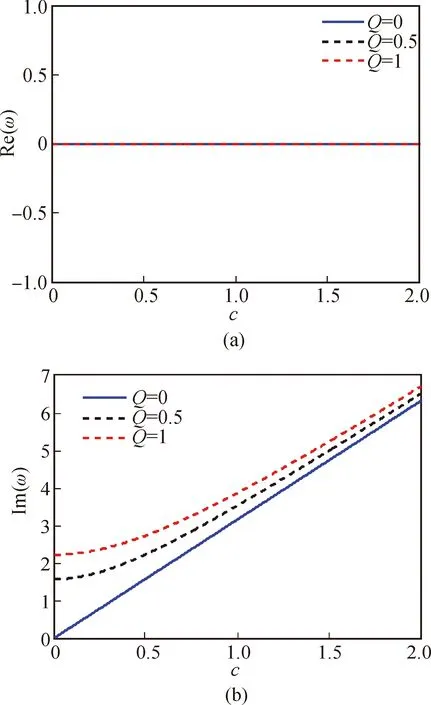
图5 L=0时无量纲复频率ω随无量纲速度c的变化曲线Fig.5 The relationship between dimensionless complex frequency and the dimensionless velocity when L=0
5 结 论
1) 薄膜的非线性振动对初始运动条件有敏感依赖性,运动条件不同,薄膜的非线性振动特性有显著差别。
2) 初始运动条件L=1和无量纲速度c=0.5,长宽比r越小,薄膜随从力越大时,薄膜越容易产生振动发散失稳现象。适当增加薄膜的长宽比,减小随从力,可有效避免大挠度非线性振动的产生。
3) 当初始运动条件L=0和无量纲速度c=0.5时,薄膜始终处于大挠度振动状态,随从力的变化不影响系统发散失稳的快慢,且该现象与薄膜的长宽比无关。
4) 初始运动条件L=1和长宽比r=1时,减小薄膜的随从力Q可提高薄膜振动失稳的临界速度,使失稳的临界速度高于薄膜的工作速度,能够有效地保证薄膜工作在稳定的状态。
5) 初始运动条件为L=0,长宽比为r=1时,薄膜始终处于发散失稳的状态,速度越大,发散失稳越快,减小薄膜无量纲运动速度c,可以有效避免大挠度非线性振动现象的产生。
