基于计算全息的衍射光学元件印模制备方法研究

武耀霞，张 锦，孙国斌，蒋世磊，弥 谦，李世杰，杨鹏飞，王玉瑾

(西安工业大学 光电工程学院，陕西 西安 710032)

引言

衍射光学元件[1]是微结构光学功能元件的一种，是基于光波的衍射理论，利用计算机辅助设计技术，并用各种微细加工工艺，在片基或传统光学器件表面刻蚀产生两个或多个台阶甚至连续浮雕结构，形成具有极高衍射效率的纯相位光学元件。衍射光学元件因具有体积小、重量轻、易复制、衍射效率高等优点，已经引起了光学技术领域的高度重视。目前该类型元件设计和制作方法主要涉及光学全息、计算全息和光刻技术。光学全息[2]是采用一束透过物体的光与参考光进行干涉得到干涉条纹，并利用感光介质记录干涉条纹，然后利用衍射使波前再现；计算全息[3-6]是基于计算全息理论设计的，主要是以数字计算和现代光学为基础，直接借助计算机的数值计算来模拟物光波与参考光波的全息干涉过程，得到数字化的离散数据，最终利用光刻技术加工出相应的光学元件；对于高精度的衍射光学元件，光刻技术利用投影物镜将掩模图形缩小成像在光敏材料表面，显影后再通过刻蚀工艺将图形结构转移到基底材料表面。然而，随着微结构表面轮廓结构的日益复杂化，目前这类元件只能实现小批量或者单件的加工，不能满足急剧增加的市场需求。近几年来，随着微加工技术的快速发展，逐渐发展起来一门新技术——复制加工技术[7-9]，该技术因具有精度高、成本低、生产批量化等特点，被广泛应用。然而，目前印模的制备方法主要是通过微电铸技术、传统光刻技术和复制技术等来制备印模微结构。如韩国高丽大学材料科技工程学院的Sung-Hoon HONG等人结合热压印和纳米电铸工艺在聚合物胶膜上直接电铸复制出特征尺寸为50 nm的镍模具[10]；哈尔滨工业大学罗军使用 L-edit 软件设计了菲涅尔透镜与四台阶光栅掩膜板，在硅基底上制备了线宽为 4 μm、台阶深度 307.5 nm 的四台阶光栅压印模具[11]；太原理工大学郭慧晶将软模具与纳米压印技术相结合,以普通CD、DVD和BD光盘中的聚碳酸酯层(PC层)为初始模具,并采用聚二甲基硅氧烷(PDMS)复制其微结构从而形成软模具[12]。但这些方法制备印模不仅工艺复杂，而且误差比较大，同时不能满足非对称多台阶结构的制备。

针对相位型衍射光学元件印模设计，提出了基于计算全息技术，利用MATLAB仿真非对称多台阶印模微结构的台阶尺寸，并根据仿真数据采用单点金刚石车削技术直接加工出印模的方法，在理论上实现了对非对称多台阶衍射光学元件印模的制备，最后采用紫外固化纳米压印技术[13-14]实现了4台阶印模的复制，并对复制样品进行了图像再现。首次尝试设计制造计算全息编码的衍射光学元件印模，对后续衍射光学元件的加工制备具有指导意义。

1 设计原理

相位型衍射光学元件印模设计的理论基础是计算全息，其实质是用离散的数值储存来代替光学仪器的实际记录，实现原理是借助于计算机的数值计算来模拟物光波与参考光波的全息干涉过程，生成数字化的全息图，将数据取反(大值与小值的互换)即可得到相应的印模数据。本文利用基尔霍夫衍射公式对衍射微光学器件的衍射场分布进行数值计算，并在傅里叶变换的迭代算法(GS)的基础上求得衍射光学的相位分布以及在和光轴垂直的某一输出平面上的预定光强分布[15]。二维典型衍射光学系统如图1所示，其中λ是垂直入射光波的波长，Zd为衍射距离，Dx为衍射光学器件在x方向的尺寸，并将坐标原点置于器件的几何中心，Dξ为期望输出图样在ξ方向的尺寸，且在ξ方向输出图样几何中心的坐标为ξc，另外输入/输出平面内的抽样间距严格遵循抽样定理。

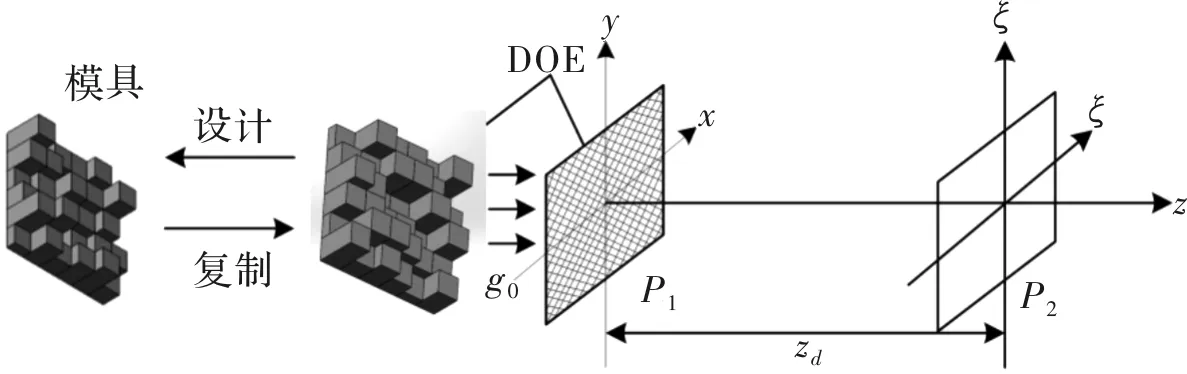
图1 基于衍射光学器件DOE的光学系统Fig.1 Optical system based on diffractive optical device DOE

已知计算全息图可由物光波和参考光波叠加形成，记录平面上的物光波和参考光波可以写成数学形式[16]：

O(x,y)=O0(x,y)·exp(jφ(x,y))

(1)

(2)

干涉场光振幅为物光波和参考光波两者的相干叠加，则干涉场光振幅U(x,y)为

U(x,y)=O(x,y)+R(x,y)

(3)

在得到用参考光波和参考光的共轭光波照射全息图的衍射光波后，利用精细化设计的抽样原则得到输入平面与输出平面的抽样间距与抽样点数，结合MATLAB程序，就可以得到相位型全息分划板的印模尺寸参数。

2 参数初始化

实现相位型衍射光学元件的印模制备，主要在于对相位型全息图的采样间距和采样点数的确定以及MATLAB程序的设计，本文选用叠心图案作为物进行模拟仿真，如图2所示。

图2 叠心图案Fig.2 Stacking pattern

根据图1的成像原理，设计的衍射相位印模元件大小：Dx×Dy=6 mm×6 mm，其中Dx为计算全息图在x方向的尺寸，Dy为计算全息图在y方向的尺寸；衍射距离：zd=750 mm；期望再现图样的尺寸的大小：Dξ×Dζ=6 mm×6 mm，其中Dξ为计算全息图在ξ方向的尺寸，Dζ为计算全息图在ζ方向的尺寸；入射光波波长：λ=632.8 nm。令ξc=ζc=0，其中ξc为ξ方向再现心形图案的几何中心，ζc为ζ方向再现心形图案的几何中心。

根据已有的精细化设计时的抽样原则，可得出输入平面与输出平面的抽样间距与抽样点数[17]。即:

Δx=Δξ=0.381 5Δx0=0.381 5λ×

Δx=Δζ=0.381 5Δy0=0.381 5λ

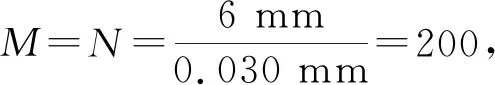
假设记录介质的折射率为n，则光程与相位之间的关系为

(4)

式中φ为纯相位。根据(4)式，可得到记录介质表面微结构的高度h为

(5)

将(5)式中求取的表面微结构高度取反(大值与小值的互换)，即为印模的表面微结构高度尺寸。

3 数值模拟

设计的相位型衍射光学元件的相位以N=2N等级来近似，根据采用的N值不同(台阶数不同)，再现图像的质量也会不同，由于通过MATLAB获取的相位型全息分划板相位是一组数据量较大的离散阵列，本文主要讨论N=2,4,8,16这4种情况下印模的表面结构高度h和图像再现质量。衍射光学元件表面高度轮廓分布及局部放大图如图3所示。相应的微结构表面空间记录介质高度h如图4所示。

从图4中可以看出，通过MATLAB完全可以实现对不同台阶数相位型衍射光学元件表面高度轮廓的仿真计算，采用不同的灰度值来表示不同的台阶高度，而且它们之间的排列也是杂乱无章的。针对不同台阶数的衍射光学元件进行图像再现情况如图5所示。

由图5可知，选用不同台阶数设计的衍射光学元件再现图的质量差异比较大，2台阶型的再现图只能大致呈现出原图轮廓，质量最差，8台阶型和16台阶型再现图能够清晰地呈现出原图像，其中16台阶型再现图质量最好，但制备相位型衍射光学元件的过程中台阶数越高工艺越复杂，精度越低，费用越高，因此要根据设计精度要求等，选用合适的台阶数来制备相位型衍射光学元件。根据不同台阶的高度值取反后，可得相应印模微结构表面高度h量化数值。如表1所示。

图3 衍射光学元件表面高度轮廓分布及局部放大图Fig.3 Height profile distribution and partial enlargement of surface of diffractive optical element

图4 衍射光学元件表面空间记录介质高度图Fig.4 Height chart of surface recording medium for diffractive optical elements图5 不同台阶数的相位型衍射光学元件计算模拟再现图Fig.5 Computational simulation and reconstruction of phase-type diffractive optical elements with different step numbers

表1 印模空间高度数据 nm

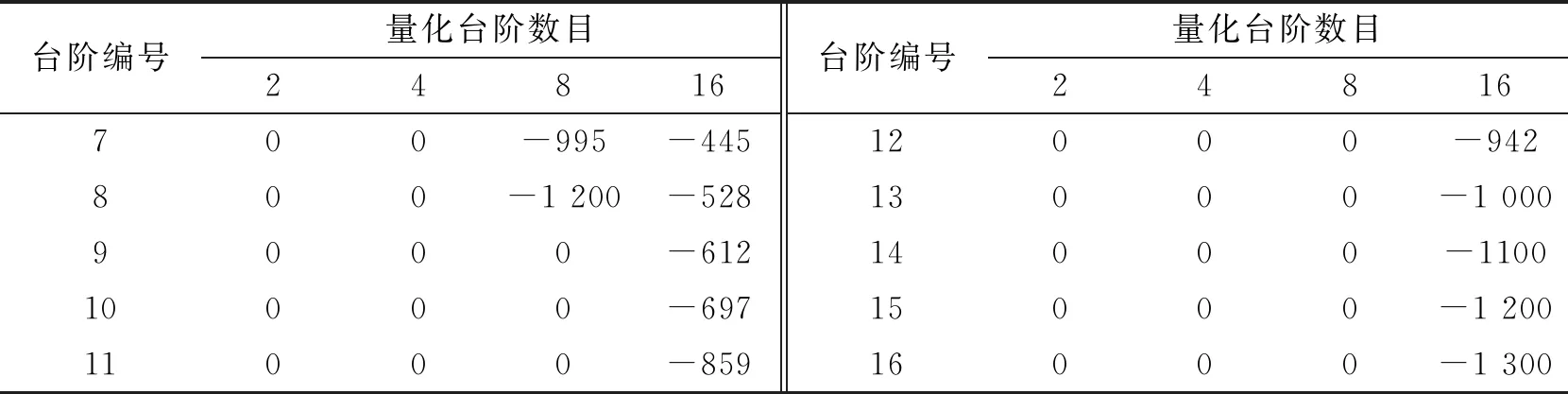
续表

4 印模制备

从上述数据及再现图可以得出:量化台阶数目越多，再现图像越接近于原来的物体。由于最小特征尺寸已达到微纳米级别，考虑到加工的难度，本文采用单点金刚石车削技术分别选取量化数目为2台阶和4台阶的数据进行印模加工。通过MATLAB将两种台阶的高度仿真数据.mat格式转变成数据流文本.txt格式，该格式主要包括3列数据；第1列数据表征X轴对应的坐标点，第2列数据表征Y轴对应的坐标点，第3列数据表征C轴对应的坐标点(即微观结构高度)。利用快刀加工的方式，主要是通过FastCom FTS Base Plot V1.5.0软件将得到的.txt数据转换成.dat格式，并生成datfilename.h, precitechXY.c和precitechFCXY.c格式文件。最终运行控制刀具轨迹坐标的程序，进而制备相应台阶数的衍射光学元件印模。2台阶相位型衍射光学元件表面高度分布以及表面轮廓如图6所示。4台阶相位型衍射光学元件表面高度分布以及表面轮廓如图7所示。

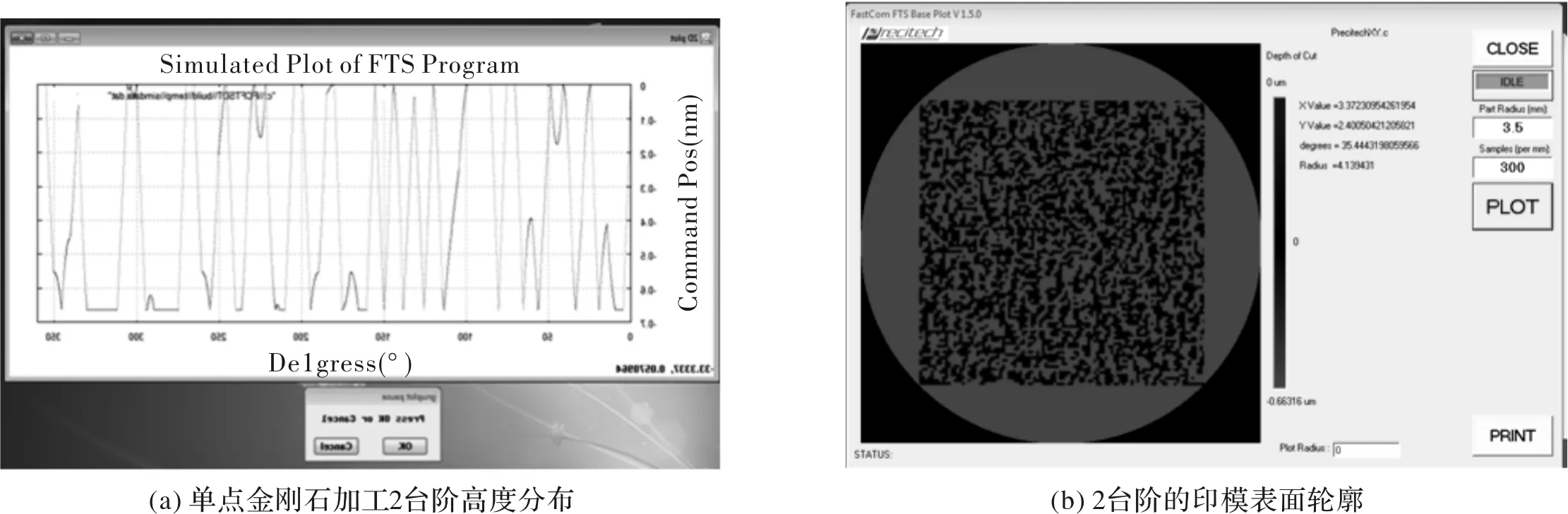
图6 2台阶相位型衍射光学元件表面高度分布以及表面轮廓Fig.6 Surface height distribution and surface profile of2-step phase-type diffractive optical elements

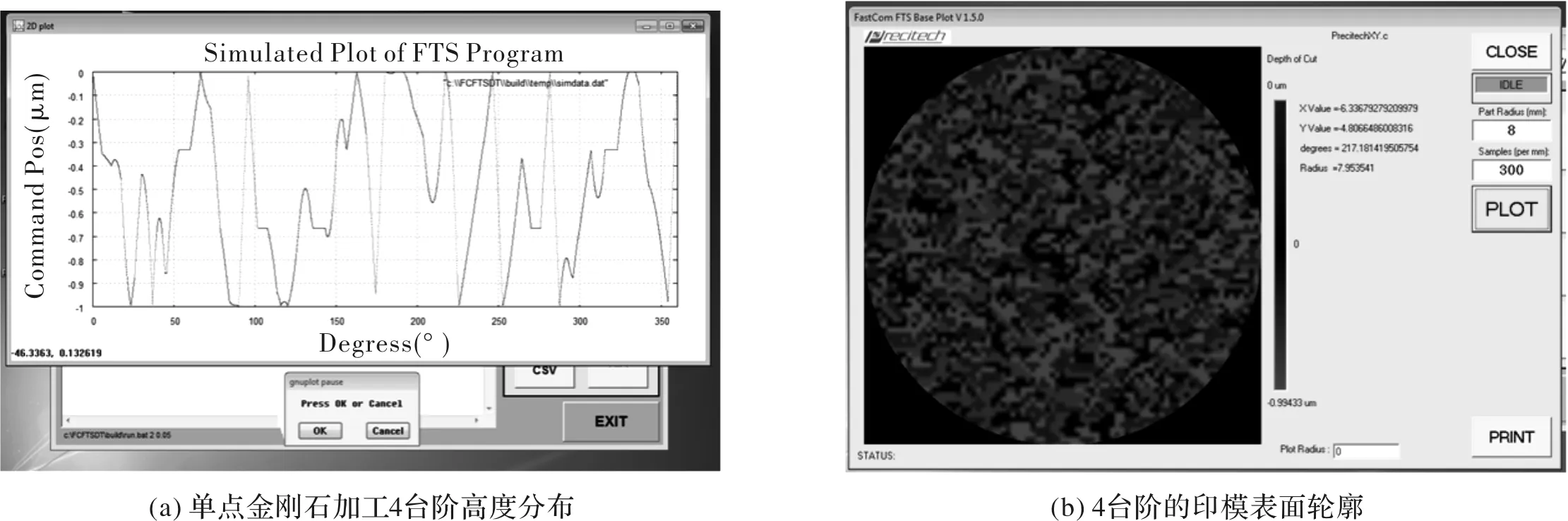
图7 4台阶相位型衍射光学元件表面高度分布以及表面轮廓Fig.7 Surface height distribution and surface profile of4-step phase-type diffractive optical elements

由图6、7可知，采用单点金刚石车削技术制备相位型衍射光学元件印模时，虽然制备的印模整体性满足要求，但产生的台阶没有达到期望中的规则形状，并且随着台阶数的增加，这种现象越明显，因为制备元件的特征尺寸较小，使快刀加工过程中产生了误差，这受限于目前单点金刚石设备的先进程度。因此，在满足设计精度要求的前提下，可采用低台阶数来实现印模的制备。

5 试验验证

为了验证印模复制的样品是否能达到理想要求，对于4台阶印模进行了样品复制。试验采用紫外固化纳米压印技术来实现样品制备，其中紫外光聚合物采用能在空气中快速固化的巯基-烯紫外光固化材料[18]，经过压印、填充、曝光、脱模等一系列过程后，直接得到4台阶复制样品。对该样品进行图像再现，如图8所示。

图8 4台阶相位型计算全息再现叠心像Fig.8 Reconstruction of stacking pattern ofreplicated-step phase-type CGH

从图8可以看出，4台阶复制样品很好地再现了原图像，这也说明通过计算全息法能实现非对称衍射光学元件印模的制备。

6 结论

在计算全息技术理论基础上，研究了相位型计算全息的工作原理和设计方法，建立了相应的光学系统和衍射光波模型，设计了求取印模相位结构的算法流程。选用叠心图案作为原始图像，通过MATLAB仿真模拟了相位型衍射光学元件印模的相位信息以及表面微结构形貌，获取了印模空间高度数据以及表面结构分布，利用单点金刚石车削技术，分别得到尺寸为6 mm×6 mm的2台阶和4台阶相位型衍射光学元件印模，并通过紫外固化纳米压印技术验证4台阶印模的可行性。印模的理论计算和以及复制样品模拟再现像的结果表明，在未考虑加工误差的条件下，所提供的这种相位型衍射光学元件印模的设计方法是可行的。目前，已经完成了8台阶、16台阶等高台阶印模的设计，但其制备受限于目前单点金刚石设备的先进程度，不能加工出相应的元件。综上所述，采用文中设计流程能够实现对相位型衍射光学元件印模的制备，为后期多台阶非对称型衍射光学元件印模的制备打下了坚实的理论基础。