圆光栅测角系统误差分析与修正

张文颖,朱浩然

(1.吉林工程技术师范学院 量子信息技术交叉学科研究院，吉林 长春 130052；2.吉林省量子信息技术工程实验室，吉林 长春 130052；3.长春理工大学 电子信息工程学院，吉林 长春 130022)

引言

圆光栅测角系统由于体积小、精度高，广泛应用于航空航天、导弹跟踪制导和机器人等领域。由于机械加工和安装等过程会使圆光栅测角系统产生误差，不能达到其标称精度。为了提高测角精度，通常采用增加测角系统中读数头个数的方法，但是其对每个读数头安装的一致性要求较高，且增加了系统的成本。误差补偿也是提高测角精度的一种方法，日本国家计量院自主研发了自校准转台标定系统 ，由于其处理方法是在时域内进行，所以对编码器采集到的数据要求不高，便于系统实现小型化[1]。德国联邦物理研究院 提出了PFDM(prime factor division method)模型[2]，利用这种标定模型校准后的精度小于0.8″[12]。中国计量科学研究院提出了一种基于等分平均原理的校准方法，8个编码器均布于码盘上，测角误差为0.03″。以上方法可抑制部分测角系统的误差，为了提高误差补偿效果，研究测角系统的误差产生机理是首要问题，有助于后续有针对性的进行误差补偿，提高测角系统的精度。

本文针对不同类型的误差进行具有针对性的分析，基于误差的特性和表现形式，从谐波角度对测角系统中的刻划误差、光电信号误差、变形导致的误差建立相应的数学模型，具体分析对测角系统影响较大的偏心误差和倾斜误差，建立数学模型并仿真分析，为提高测角精度提供了理论基础。

1 圆光栅测角系统

标尺光栅与指示光栅共同组成圆光栅[3]。在进行角度测量时，转轴与标尺光栅一同转动，但指示光栅位置不变。连续变化的莫尔条纹由两种光栅间的相对转动构成，利用莫尔条纹移动的数量完成对圆光栅的测角任务[13]。标尺光栅的栅距和指示光栅的线宽相等，假设忽略光栅衍射的现象，依据透光与遮光原理可知，通过两块光栅后形成一个三角波的光能量分布[4]，如图1所示。然而在实际应用时，因为光栅的衍射作用以及刻划误差、指示光栅的间隙与标尺光栅等因素，光能量实际分布为一个近似的正弦函数。应用圆光栅时，利用统计莫尔条纹平移数量的总和完成角位移量的测量。

图1 莫尔条纹图形Fig.1 Moire fringe pattern

2 误差分析

导致圆光栅测角误差的原因主要有光栅环的刻划误差、光电信号误差、偏心误差和倾斜误差[5]。其中，刻划误差和光电信号误差是高频测角误差。

2.1 刻划误差

在刻划圆光栅环上的栅线时，实际栅线位置与理想栅线位置存在偏差，即为刻划误差。假设理想刻线与实际刻线的位置偏差为±30 mm，若直径D为299 mm，换算成角度的刻划精度δgra为

(1)

式中δ为刻划误差，刻划精度为±0.5″。

2.2 光电信号误差

光电信号误差作为引起读数头误差因素中最为关键的一项，其本质为在插值操作中信号的非正交、不等幅、直流电平漂移所产生的非线性误差[6]。光电信号误差是系统中频率最高的误差成分，其由“偏移量”和“椭圆度”构成。

理论上，理想条件下莫尔条纹的光电信号应为正弦函数，即莫尔条纹的正弦性[14]。然而现实环境下，存在诸多外界因素，实际的光电信号是由基波与高次谐波相加的形式组成[15]，即：

(2)

光电信号误差表达式为

(3)

式中：ΔU(x)为各次谐波；x为光栅位移；U0为光电信号叠加的直流电平；Um为信号幅值；p是光栅栅距。谐波导致光电信号为非正弦信号，最大波动为

(4)

2.3 偏心误差

偏心是指光栅环的中心与转轴运动中心不重合，其主要由装配间隙等引起圆光栅几何中心和装配后的旋转中心不重叠和轴系运动导致的[7]。偏心误差是导致测角系统误差的主要因素，通常为测角系统误差的50%以上[8]。

圆光栅理想旋转中心是O点，半径是R，偏心量是e，O是坐标原点，偏心方向为x轴方向，建立如图2所示直角坐标系xoy。令O′点为圆光栅实际旋转中心，A′为圆光栅理想位置上的点，A为圆光栅实际运动轨迹上的点。利用圆光栅转过的弧长与圆光栅半径作商，即可得到测角系统测得的角度值。因为偏心造成圆光栅上的点与圆光栅理想旋转中心O的距离周期性变化，所以，利用弧长L和角度θ之间的数学关系，能更精确表示测得的角度值。

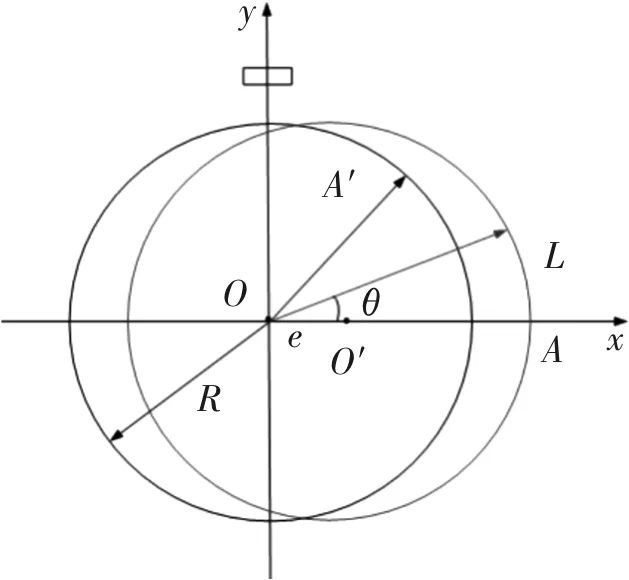
图2 圆光栅偏心示意图Fig.2 Diagram of circular grating eccentricity

如图2所示，B为圆光栅实际运动轨迹上一点，设∠AOB=θ，圆光栅转过的弧长为L。如图3所示，在极坐标系中，弧长L与极径r之间关系可以表示为

(5)

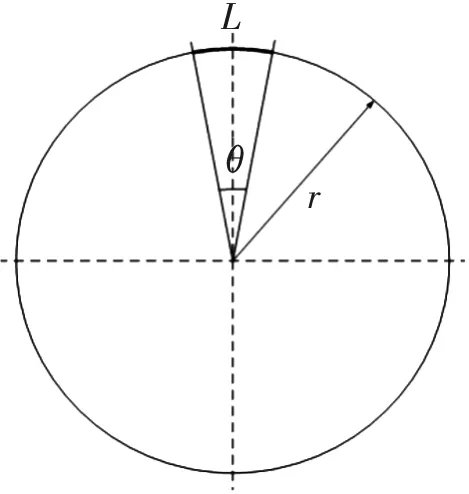
图3 弧长和角度关系图Fig.3 Relationship diagram between arc length and angle

设A点坐标为(x,y)，那么有：

(x-e)2+y2=R2

(6)

由于r>0，R>e，则：

(7)

利用幂级数展开和保留二阶小量，能够获得圆光栅上A与B之间的弧长为

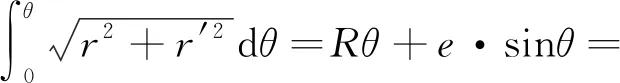
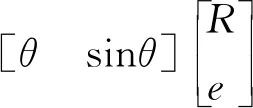
(8)

角度误差为

(9)

在0°～360°的测量范围内，以10°为间隔读取一个测量值，偏心量0≤e≤0.9 μm，r=54 mm时，偏心误差的变化趋势如图4所示。

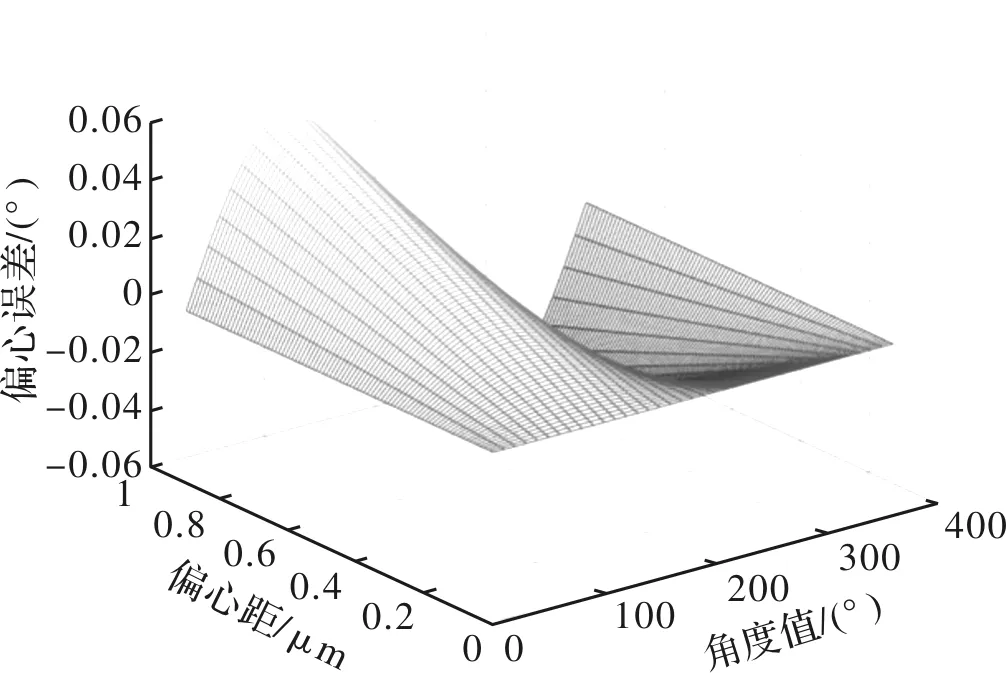
图4 偏心误差Fig.4 Eccentricity error

角度误差的最大值为

(10)

如图5所示，有一个旋转初始角θ0，令O′点为坐标原点，建立直角坐标系x′o′y′，弧长可表示成：

L=-Rθ0+Rθ+e·sinθcosθ0-e·cosθsinθ0

(11)

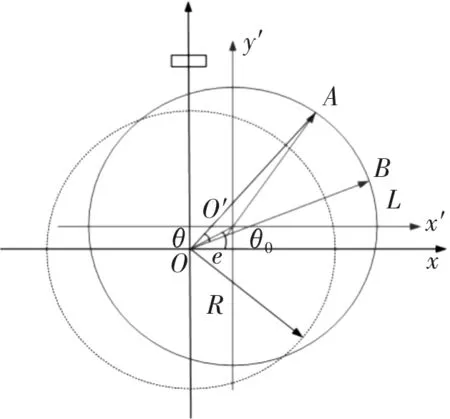
图5 初始角偏心示意图Fig.5 Diagram of initial angular eccentricity

角度误差为

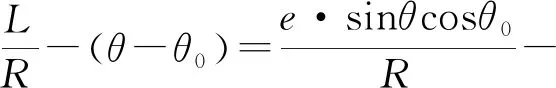
(12)

由(11)式和(12)式能够发现，当圆光栅有偏移量时，在弧长与角度间的关系中会产生谐波误差，圆光栅半径R为一次项系数，在角度误差中也会有待测角度的谐波成分，并且为一次谐波。

2.4 倾斜误差

光栅环的倾斜是二阶测角误差的一个重要来源，其会使莫尔条纹的宽度与数量一同产生变化[9]。光栅环产生倾斜的主要原因有以下两种：安装倾斜和轴系运动过程导致的倾斜[10]。图6所示为安装倾斜示意图。令光栅环相对读数头所在平面的倾斜角为γ，光栅半径是r，那么光栅旋转过程中导致莫尔条纹移动的最大值是：

ΔB=±rsinγ

(13)

则莫尔条纹移动数为

(14)

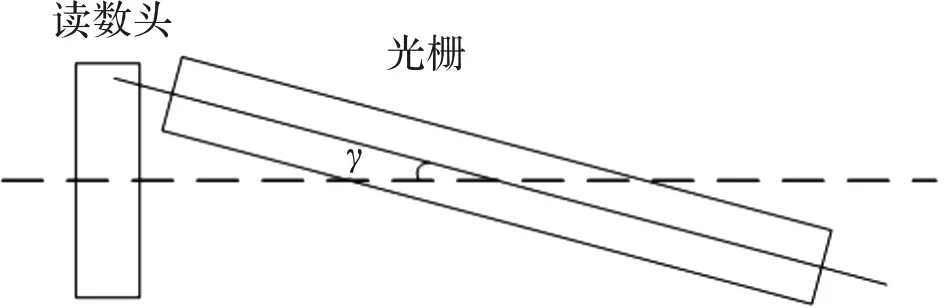
图6 安装倾斜示意图Fig.6 Diagram of tilt installation

一般情形下，由于栅线角较小，栅线角θ、光栅栅距ω和莫尔条纹宽度B满足下式[11]：

(15)

在光栅平移一个栅距ω的情况下，莫尔条纹会平移一个条纹宽度B，所以，利用莫尔条纹平移的数目N可计算出光栅转动量s：

s=N·ω=N·Bθ

(16)

令光栅的半径为r，则光栅转过的角度β表达式为

β=s/r=N·Bθ/r

(17)

将(14)式带入(17)式，得到安装倾斜导致的角度误差为

(18)

在0°～360°的测量范围内，以10°为间隔读取一个测量值，当倾斜角0°≤γ≤1°时，倾斜导致的误差变化趋势如图7所示。

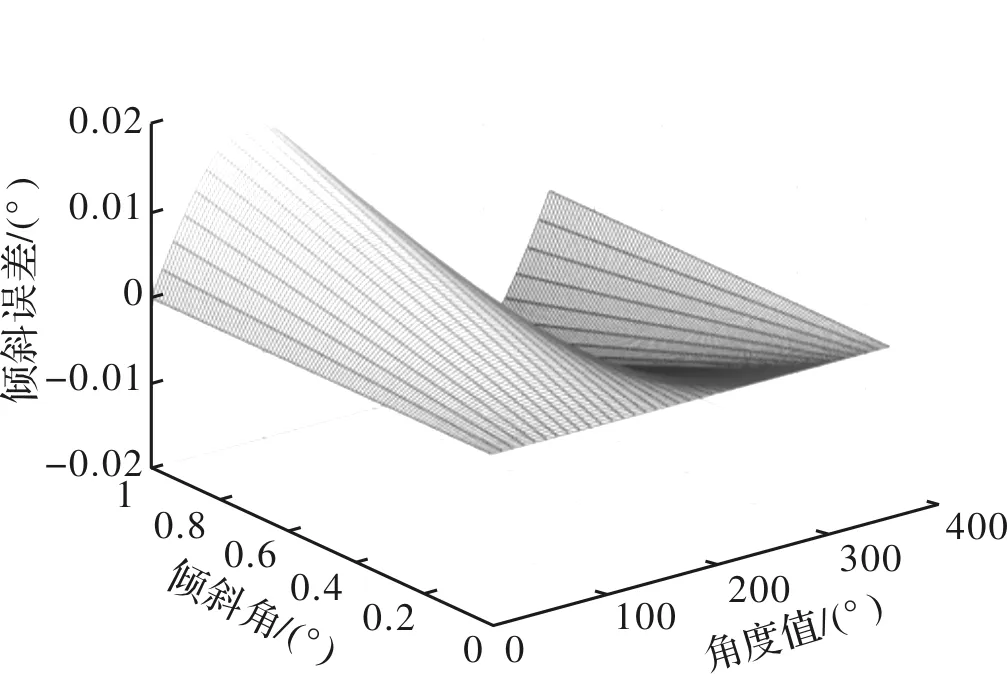
图7 倾斜误差曲线Fig.7 Curve of tilt error

3 实验

3.1 实验系统

为了分析引起圆光栅测角系统误差的各类误差因素并进行修正，搭建实验系统，实验中选用Renishaw公司SiGNUMTM系列金属圆光栅测角系统，如图8所示。为了获得测角误差，利用二等8面棱体和CSZ-1型CCD双轴自准直仪配合使用，以获得测量真值。

图8 测角系统Fig.8 Angle measuring system

3.2 误差修正

图9为金属圆光栅测角系统原始误差曲线。由图9曲线可知，在0°～360°的范围内，峰-峰值为-70.51″和63.67″，测角误差为134.2″。

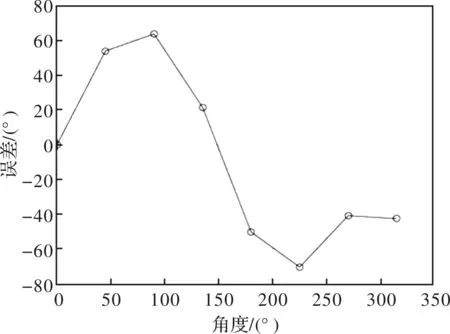
图9 误差曲线Fig.9 Error curve

RESM系列金属圆光栅栅距为20 μm，有效直径为52 mm。刻划误差为±3.97″，光电信号误差为0.32″，圆光栅测角系统工作过程中，旋转轴系与光栅盘的偏心量为e=7 μm。由(9)式可知，当sinθ=±1时，偏心误差最大为

由此可知，偏心是导致测角系统误差的主要因素。

由于角分辨率为0.004″，莫尔条纹间距为B=0.286 5 mm，当光栅旋转一个栅距ω时，莫尔条纹移动一个条纹宽度B，由(17)式计算得到θ=0.36″，光栅由于在安装、轴系旋转过程中，倾斜量为8 μm，所以光栅环的倾斜角为63.47″，带入(9)式，可得安装倾斜误差为Δβ=±0.32″。

利用获得的刻线误差、光电信号误差、偏心误差和倾斜误差修正原始误差曲线，修正后圆光栅测角系统的误差为32.23″。

4 结论

基于误差的特性和表现形式，本文从谐波角度对圆光栅测角系统中的刻划误差、光电信号误差等建立了相应的数学模型，并对测角系统中误差较大的偏心误差和倾斜误差进行了具体的数学建模与仿真分析。搭建了金属圆光栅测角系统，对偏心误差和倾斜误差进行了具体分析。实验结果表明，测角系统测角误差为134.2″，修正后误差为32.23″，为后续误差补偿提供了依据。