基于修形的摆线针轮啮合加载接触分析*
2019-05-24张跃明纪姝婷
张跃明,杨 青,纪姝婷
(北京工业大学 机械工程及应用电子技术学院,北京 100084)
0 引言
摆线针轮之间的齿面加载接触性能是影响RV减速器寿命及传动精度的重要因素,修形后的摆线轮与针轮啮合过程的弹性变形对其接触刚度、齿间载荷分布影响较大。
很多学者对摆线针轮行星传动机构展开了研究,已有研究主要集中在摆线针轮传动的几何及运动学分析[1-2]、动力学建模[3]、刚度计算[4]、传动精度[5]及修形优化[6]等方面,然而对摆线轮的接触变形弹性扭转角模型的建立有待深入,故本文针对修形后的摆线针轮行星传动机构中摆线轮的弹性扭转角展开了研究。在考虑到针摆传动机构齿廓接触变形的基础上,建立有限元模型,利用软件仿真分析摆线针轮齿面接触受力及啮合过程中各齿对的载荷分布情况,分析了其齿面的应力分布情况,计算了加载情况下摆线轮的弹性转角,为提高RV减速器的传动精度及使用寿命的提高提供理论依据。
1 摆线针轮传动原理分析
1.1 RV减速器传动原理分析
RV减速器是一种二级减速器[7],由渐开线行星传动机构和摆线针轮行星传动机构两级减速机构组成。其中,摆线针轮行星传动机构由针轮、针齿壳、2个摆线轮和2个双偏心轴组成。按运动要求,一个摆线轮就可传动,但为使输入轴达到静平衡和提高承载能力,对于一齿差摆线针轮行星传动,常采用两个完全相同的奇数齿的摆线轮同时装在两个双偏心轴上,两轮位置正好相差180°。

图1 RV减速器爆炸图
由图2所示,在针齿壳固定的情况下,伺服电机带动第一级渐开线太阳轮1转动,太阳轮1带动渐开线行星轮2自转,由于行星轮2与曲柄轴之间是花键连接,所以曲柄轴在行星轮2的带动下自转,曲柄轴带动摆线轮4公转,由于摆线轮与针轮相啮合,摆线轮4作自转,进而带动两个曲柄轴公转,保持架与输入轴同轴,曲柄轴的公转带动保持架自转。摆线轮的自转作为减速器的最终输出,故摆线轮与针轮啮合特性对RV减速器传动有着至关重要的影响。
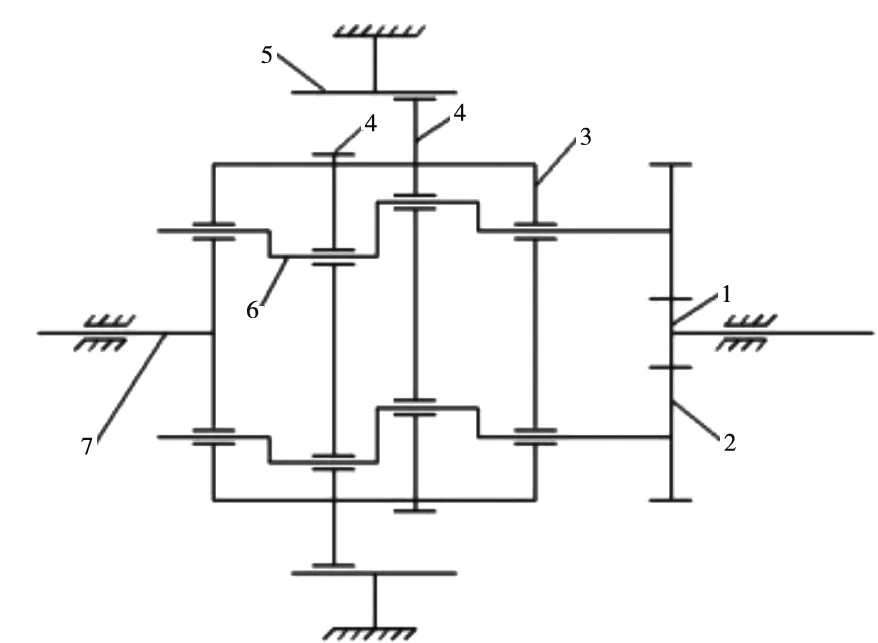
图2 机构运动简图
1.2 摆线针轮传动
图3为摆线针轮装配图。在理想传动过程中,一半的摆线轮齿廓参与啮合传动[8]。为了合理装拆,便于润滑,必须对摆线轮齿廓进行合理修形。最常用的修形方式为等距修形与移距修形的组合修形方式。当不考虑接触变形情况下,任一时刻只有一个摆线轮齿首先与针齿接触,其余齿对间都存在初始间隙Δ(φ)i。若考虑摆线轮与针齿间的接触变形,在力矩作用下,摆线轮与针齿会在接触点的公法线方向产生接触变形,接触变形直接影响齿面受力状态,从而使摆线轮整体产生弹性扭转角β,进一步影响机构的传动精度。

图3 摆线针轮装配图
2 摆线针轮有限元模型
2.1 摆线针轮实体建模
Ansys Workbench虽然具有强大的几何建模功能,但对于复杂形状的模型,实体建模是个难点,故本文利用Pro/E软件对减速机的关键部件摆线轮与针轮进行建模。本文主要研究摆线轮与针轮的齿面接触特性,因而可对摆线轮、针齿壳的一些结构进行简化,以缩短有限元计算时间。
摆线针轮传动机构具有多齿啮合的特点,为提高有限元运算效率,可把针齿与针齿壳看作一个整体进行建模。由于机构中存在一对啮合相同的摆线轮,因而仅以一片摆线轮与针齿啮合作为对象展开研究,并使针齿长度与摆线轮宽度相等。简化后的摆线轮、针齿壳模型如图4所示。然后将Pro/E实体模型输出为IGES文件并导入AnsysWorkbench中进行相关的零件材料属性设置,建立有限元模型。

(a) 摆线轮简图 (b) 针轮简图 (c) 装配简图 图4 摆线针轮实体模型
2.2 网格划分
网格划分的质量和密度对有限元分析的计算结果影响较大,网格的质量直接影响到最后的分析结果,为保证计算效率及精度,需要对模型合理划分网格。考虑到本文只要分析摆线轮与针轮接触面的受力情况,采用自动网格划分,同时对网格大小及质量进行控制,防止畸变。在此基础上对可能接触区域进行网格局部细化。网格划分如图5所示,划分后节点数为197131,单元数为98429。

(a) 网格划分 (b) 网格划分局部图 图5 网格划分
2.3 边界条件
由RV减速器摆线针轮传动原理可知,摆线轮会随着偏心轴做公转运动,由于摆线轮与针齿间的啮合,迫使摆线轮自转,因而需在摆线轮上施加力矩模拟偏心轴对摆线轮的作用力偶,故对摆线轮进行静力学分析时,应在摆线轮上施加力矩,针轮固定不动,施加完全约束。
2.4 摆线轮与针轮的接触定义
为使计算精确,需确定哪一齿对首先进入接触,对进入啮合的齿对设置接触对,建立接触间隙模型。
在传递力矩过程中,修形后的摆线针轮各齿的初始间隙计算公式[9]为:
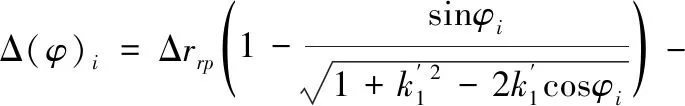
(1)
当考虑接触变形时,摆线轮与针齿间的接触变形为:
δi=li·β(i=1,2,...,Zp/2)
(2)
其中,li是第i个针齿啮合点的公法线或待啮合点的法线到摆线轮中心的距离,即摆线轮齿第i处的接触作用力的力臂;β为摆线轮弹性扭转角;δi为摆线轮与针齿间的接触变形。
对于修形后的摆线轮,加载后,轮齿必须克服初始间隙才能接触参与传递转矩,即总变形大于初始间隙时,摆线针轮齿对进入啮合。
以RV-20E为例,各参数为:rp=52.5mm,rrp=2.25mm,zc=39,zp=40,a=1mm,力矩为Tc=167N·m,材料为GCr15,弹性模量为2.06E5MPa,泊松比为0.3,密度为7.8E2kg/mm3,以摆线针轮转臂与Y轴正方向重合位置为初始啮合位置。由公式(1)、式(2)结合Matlab软件计算处理可得出初始间隙及总变形如表1所示(取对称轴与摆线针轮转臂重合的齿记为1号齿,逆时针依次编号)。
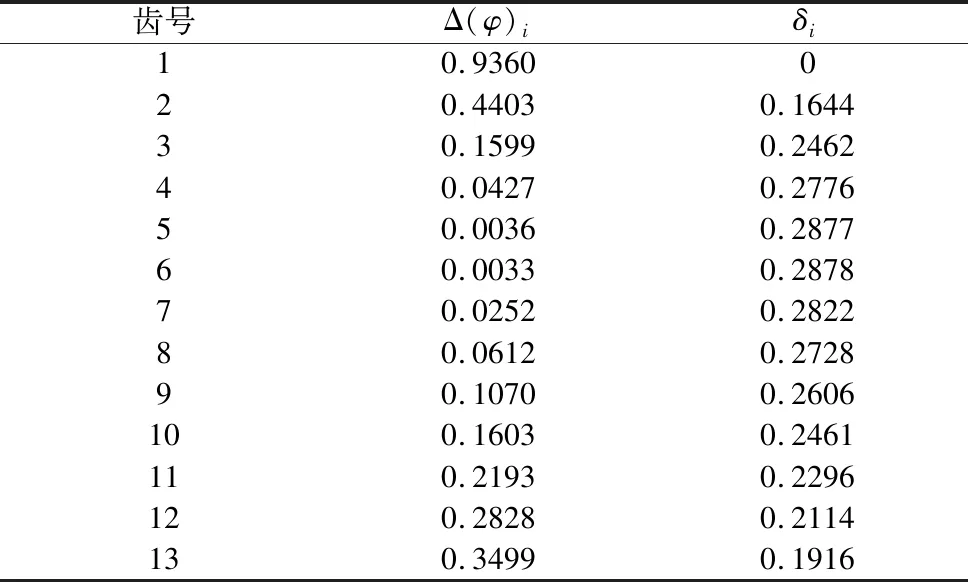
表1 针摆啮合各齿变形量与初始间隙大小(部分值)
由表1可知:针轮从第3号齿开始啮合,第11号齿啮出,中间各齿处于啮合状态。故对摆线针轮有限元模型中的第3号齿对到第11号齿对间建立接触对。在创建接触对时,一般选择凸面为接触面,凹面为目标面。针摆传动中针齿接触面定于为接触面,摆线轮接触面定义为目标面,接触类型为Frictional。
3 摆线针轮静力分析
3.1 齿面接触应力有限元分析结果
由于有限元模型仅以一片摆线轮为研究对象,故在摆线轮上施加的逆时针转矩为:T=0.55Tc。Tc为施加于输出支撑架间的转矩。
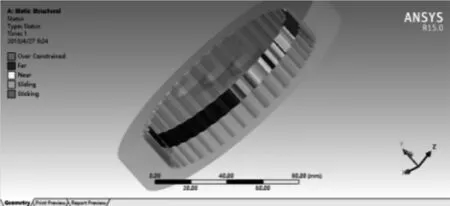
图6 接触区域
由图6可知,针摆加载传动过程中有7对齿处于接触状态,说明第3个齿与第11个齿处于临界状态,从第4个齿到第10个齿处于啮合状态。以摆线轮第8号齿为例,图7为单齿对接触区域齿面局部放大图,X轴沿齿廓曲线方向,Y轴沿齿宽方向,原点位于齿顶部分。
图7 接触区域局部放大图
沿齿宽方向均匀截取8个法截线,在法截线上以齿顶点为1号节点,从左向右依次均匀提取曲线上10个节点的接触应力,绘制曲线。如图8所示,在此位置上,由于摆线轮修形使得齿顶部分接触应力较小。节点2处应力较大且此节点恰好位于摆线轮一个齿的齿廓曲线拐点附近。6号节点到10号节点应力逐渐增大,且截面1到截面5总体接触应力逐渐增大,截面6到截面8总体接触应力逐渐减小。
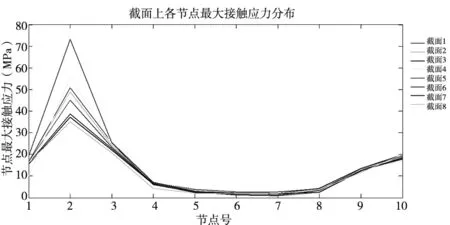
图8 Y轴各截面上节点接触应力分布图
沿齿廓曲线方向截取8个法截线,均匀提取曲线上15个节点的接触应力,绘制曲线如图9所示。所有曲线的趋势都为中间应力较大两侧应力较小。
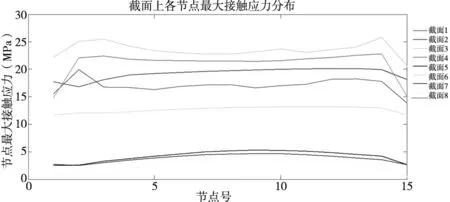
图9 X轴各截面上节点接触应力分布图
3.2 针摆传动最大接触应力分析
根据文献[13]中的摆线针轮啮合力计算公式,结合Matlab软件分析计算出摆线针轮各接触齿对理论载荷得图10。
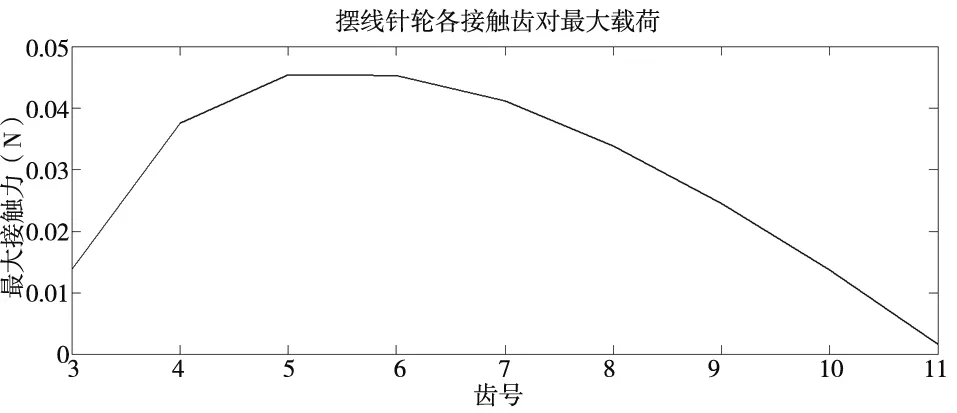
图10 加载情况下各接触齿对的理论载荷分布
在加载情况下,针摆传动过程中各接触对齿间最大理论载荷出现在第5号齿附近。
依据3.1节结论对摆线针轮有限元模型进行相关设置,得出摆线针轮齿间接触应力分布如图11。

图11 等效应力云图
用θ表示转臂(偏心轴)的转角,顺时针为正,则图11为当θ=0°时,摆线针轮啮合传动的等效应力云图,最大接触应力出现在第4号齿与第5号齿之间,与理论计算结果较为一致。如上设置不变,将摆线针轮转臂转过不同角度分别分析3个不同位置θ=30°、θ=60°、θ=90°的等效应力。

(a) 转臂转角为30°
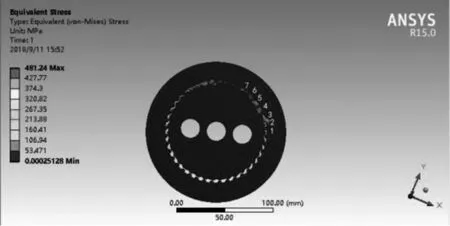
(b) 转臂转角为60°

(c) 转臂转角为90°图12 不同转臂位置摆线针轮等效应力云图
由图12可得:针摆传动最大接触应力总是出现第5号齿附近,即针齿啮合点公法线与摆线针轮转臂垂直的齿廓。
3.3 摆线轮接触变形弹性转角分析
根据以上结论,利用有限元软件,固定针齿壳,设置摆线针轮各齿对受力及其他相关参数,计算出摆线针轮传动过程中由于齿廓接触变形引起的摆线轮弹性扭转角如图13所示。

图13 摆线轮接触变形弹性转角图
给定额定转矩Tc=167N·m,计算得到摆线轮弹性扭转角为0.0041309°。将负载转矩由零增大到额定转矩,利用有限元软件计算相应的摆线轮弹性扭转角,由Workbench导出弹性扭转角数据,用Matlab软件处理得出传递的力矩大小与摆线轮接触变形弹性转角的关系图。
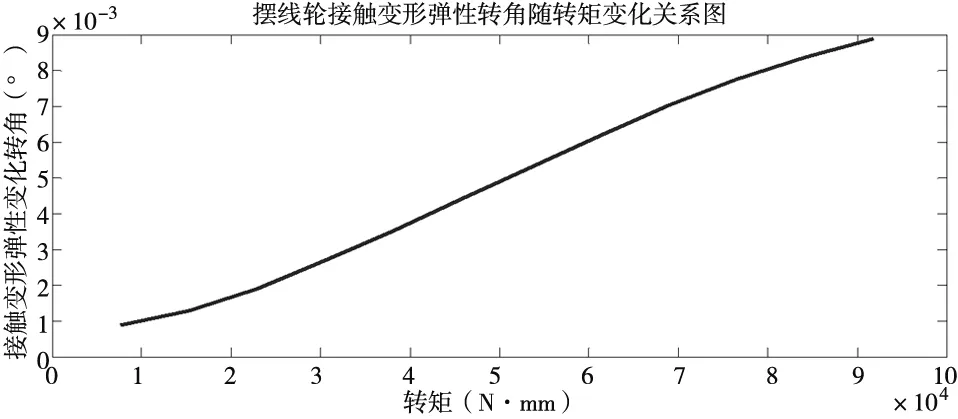
图14 转矩与变形转角的关系图
由图14可知:转矩越大,摆线轮的弹性转角越大,摆线轮的变形也越大。满载转矩条件下,摆线轮弹性扭转角达到0.247854分,这对摆线针轮机构传动精度不能忽视,因而分析摆线针轮传动需考虑弹性变形。
4 结论
在Ansys Workbench中建立摆线轮与针轮啮合的三维模型,分析了参与啮合齿面上的啮合作用力、最大接触应力和接触区域受力分析后,得到以下变化规律:
(1)有限元计算结果与理论分析对应的摆线轮齿面上作用力与接触应力具有一致的变化趋势。当摆线针轮转臂转过不同角度时,针摆传动最大接触应力总出现针齿啮合点公法线与摆线针轮转臂垂直的齿廓附近。
(2)摆线针轮啮合过程中,随着转矩增大,由于摆线轮接触变形产生的弹性扭转角会随之增大,其扭转刚度近似成线性关系,且弹性变形不可忽视。
(3)单齿对加载接触变形沿齿廓曲线方向在曲线拐点处接触应力最大;沿齿宽方向,在齿面中间部分接触应力较大。
