新型动静压转台螺旋油楔几何参数优化*

田再浩，马金奎，路长厚，陈淑江，聂玉龙

(山东大学 机械工程学院，济南 250061)

0 引言

回转工作台的润滑问题求解可以借鉴推力轴承的相关研究。近年来，学者们对轴承在不同油腔形状下的润滑性能进行了研究[1-3]，同时在摩擦学的发展进程中，螺旋楔形织构因为其优良的润滑性能也广受关注[4-8]。在对轴承表面织构优化方面，Mei-Hsia Chang等[9]根据不同的工作条件下的承载能力要求，使用共轭梯度法对轴承油腔表面形状进行优化设计。叶红玲等[10]以静压转台承载力和油膜刚度为目标函数，利用响应面方法和分层可行下降方向法对优化模型进行了求解，得到了油腔结构尺寸的最优参数。庞晓平等[11]应用非支配排序遗传算法，以最小功耗和最小侧漏流速为优化目标，对动压轴承形状地进行了多目标优化设计。张永芳等[12]采用基于序列二次规划算法和遗传算法的混合优化方法以径向滑动轴承最大承载力和最小摩擦因数为目标，对轴承凹坑织构的分布位置和结构参数进行了综合优化。孟曙光等[13]研究了操作参数及织构结构参数对深浅腔动静压轴承承载特性的影响，并使用正交实验法并结合实验对轴承的结构参数及工作参数进行了多目标优化。本文在求解优化问题方法上选用由Xin-She Yang和Suash Deb于2009年开发的新型自然启发式算法——布谷鸟搜索算法(Cuckoo Search, CS)[14]。CS算法通过Lévy Flights进行加强，相比遗传算法和粒子群算法，在优化变量的全局寻优中有着更好的收敛性和更高的搜索效率[15-16]。CS算法在部分领域中已经有着实际运用[17-19]，但是在润滑领域的优化问题中应用还相对较少。

在上述研究中，对轴承织构的优化往往局限于固定工况下，而没有考虑最优解在不同工况下的变化情况。本文以一种新型螺旋油楔动静压转台为研究对象，以其动压承载力为目标函数，改进其表面螺旋油楔结构参数，并探究不同工况下最优解的变化规律。通过对比本文理论计算结果和CFD仿真结果和对比优化前后的转台性能，验证了理论计算及优化方法的正确性和实用价值。

1 分析模型

1.1 物理模型

本课题组提出了一种新型差速动静压转台如图1所示，主要包括基座1、动环2、工作台3、负载4、动环主轴5和工作台主轴6。工作时工作台低速旋转，动环高转速顺时针旋转，可设动作台与动环间差动转速为ω。启动及低速阶段工作台以静压支承为主，工作阶段差动转速较大，动压支承将发挥重要支承作用。相比于静压回转工作台，工作阶段工作台与动环通过“差速运动”在动压区中产生的动压承载力能显著提高转台的承载性能，所需的供油压力也相对较小；相比于动压回转工作台，由于静压支承的存在，在启动阶段能较好地避免摩擦副中固-固摩擦导致的端面磨损。

工作台下表面为光滑平面，动环上表面织构分布——沿周向周期性分布的静压油垫及其外环的动压油楔如图2所示。r1、r2分别表示静压油垫的内径和外径；r3、r4分别表示动压油楔的内径和外径；φ1、φ2分别为静压油垫内、外近似包角；l为封油边宽；b为静压腔径向尺寸；p0表示静压油垫外压力，也为动压油楔内径处压力；pout为动压区外缘处压力。

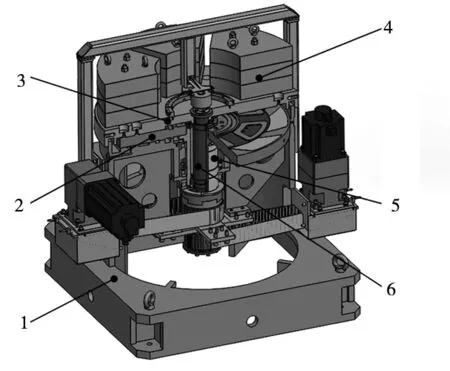
1.基座 2.动环 3.工作台 4.负载 5.动环主轴 6.工作台主轴

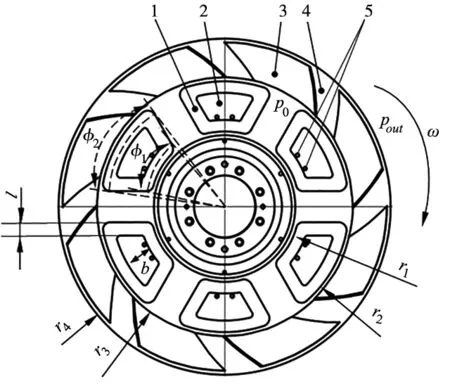
1.封边 2.液压垫3.流体槽 4.Land 5.供油孔图2 动环织构示意图

1.2 计算域模型

圆柱坐标系下螺旋油楔端面形状如图3a所示，油楔端面轮廓为对数螺旋线。螺旋线可以较好地匹配流体沿盘面运动的轨迹，加速润滑油流出转台，及时带走转台内产生的热量。对数螺旋线在极坐标下的表达式为：

r=r3e(θ-θi) cotβ

(1)

式中，θi为螺旋线起始角度；β为螺旋角。

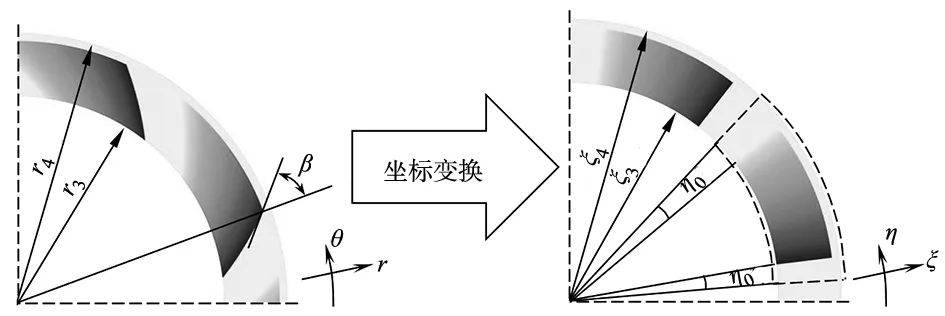
(a) 圆柱坐标系下油楔端面 (b) 边界拟合坐标系下油楔端面图3 织构形状及坐标变换

数值计算动压分布时，为保证使用网格划分对计算域离散时的计算精度，可采用基于边界拟合坐标系的坐标变换，如式2所示，将螺旋区域转化为简单的扇形。边界拟合坐标系下的油楔端面形状如图3b所示。

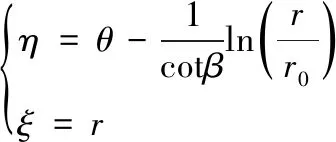
(2)

如图3b所示，选取一个油楔及其两边两个半台面为一个计算域。令油楔个数为n，则每个计算域周向包角为2π/n。动环摩擦副周向剖视图如图4所示，由图可见，台面处油膜厚度为h0，供油槽深度为h2；油楔最深处h1(以下称“楔深”)，并沿周向逆时针线性变浅最终收敛于台面。故周向动压液膜厚度可表达为：

(3)

2 控制方程及求解

2.1 控制方程

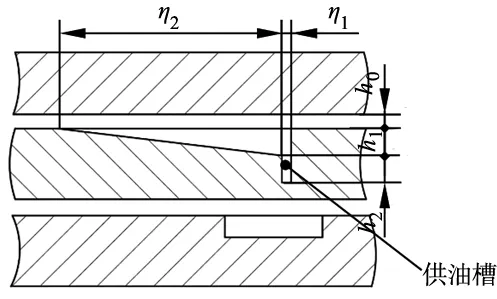
图4 摩擦副周向剖视图

在动压区薄膜润滑的状态下做出以下假设：①摩擦副中润滑剂为牛顿流体且流动状态为层流；②忽略体积力和惯性力的影响；③润滑剂在摩擦副接触面上无相对滑移；④等温假设和绝热流动。

基于以上假设，对圆柱坐标系下雷诺方程通过式(2)所示坐标变换，得到边界拟合坐标系ξ-η下的雷诺方程为：

(4)

式中，μ为润滑剂粘度；pd为液膜压力。

在液膜破裂及形成的边界采用负压置零的雷诺边界条件如式(5)所示，式中pb为液膜破裂处压力。与考虑质量守恒的JFO边界条件相比，两种边界条件在计算润滑性能时区别不大[20]，但是雷诺边界条件计算更为简便，且计算时长较短，在进行计算量庞大的优化设计中较有优势。

(5)

根据转台实际结构分析，动压区内、外径处液膜压力p0、pout为大气压，如式(6)所示。式中，pa为大气压力。

p0=pout=pa

(6)

为方便计算和分析，将式(4)进行归一化处理，得：

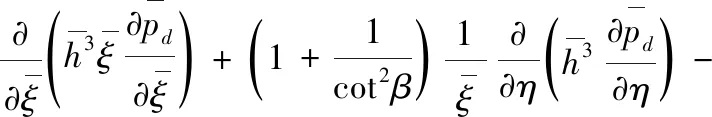
(7)

2.2 离散格式推导

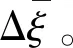
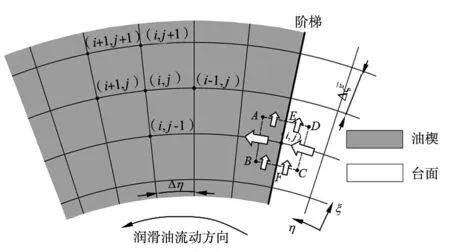
图5 计算域离散

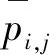
(8)

式中，

G=A+B+C+D+E

在阶梯处，由于润滑薄膜厚度导数不存在，故无法使用上述差分格式计算液膜压力。根据阶梯处网格点周围控制体积ABCD内流入和流出的润滑剂流量平衡，即：

QAB+QBF+QFC+QCD+QDE+QEA=0

(9)

得阶梯处归一化液膜压力为：

(10)

式中，

E=A+B+C+D

根据静压油垫中由节流器流入的流量和由封油边流出的流量平衡计算静压腔内压力，该压力可表示为：

(11)

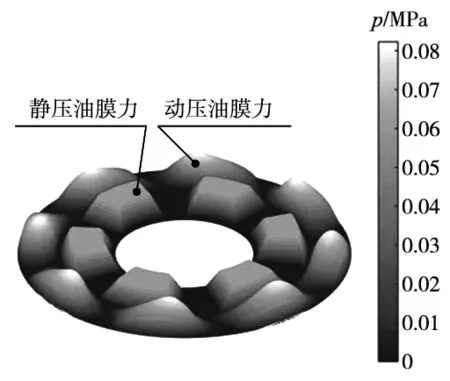
图6 动静压力分布图

2.3 润滑性能计算

得到液膜压力分布后，可以进而计算流体润滑性能如承载力、动压端泄量等，计算公式如下:

液膜总承载力为：

(12)

动压区端泄量为：

(13)

液膜平均温升为：

(14)

本文数值计算中涉及到的动环织构结构参数及润滑剂参数如表1所示。

表1 摩擦副及润滑油部分参数

3 楔形织构几何参数优化

3.1 优化设计模型

转台工作阶段动压承载力在其总承载力中占较大比重，动压承载力的大小显著受到动压螺旋油楔几何结构参数的影响，因此通过改进螺旋油楔几何参数以提高动压承载力能够有效提高转台的总体承载性能。本文优化模型描述如下。

3.1.1 目标函数

动压承载力Fd。

3.1.2 设计变量

通过比较油楔几何参数对目标函数的影响，选择动压油楔螺旋角、楔深及楔数为优化设计变量并确定优选范围。取供油压力为0.1MPa，差动转速30rpm，油膜厚度为[120,130,140,150,160]μm时，动压承载力随螺旋角、楔深及楔数的变化规律如图7所示。

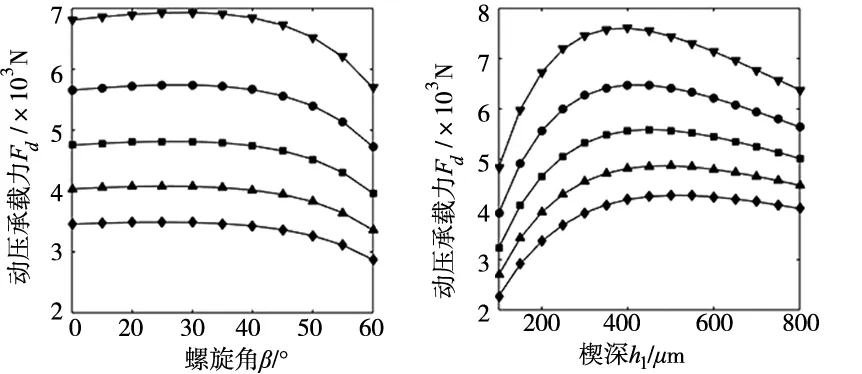
(a) 螺旋角对动压承载力的影响 (b) 楔深对动压承载力的影响

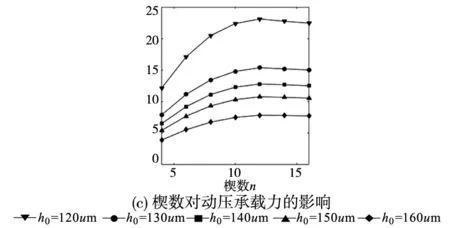
图7 螺旋角、楔深、楔数对动压力的影响

如图7a所示，取楔深为200μm，楔数为8，不同间隙膜厚下动压承载力随螺旋角β的增大呈先增大后减小的趋势，且膜厚越小，动压承载力变化范围越大。最终选定螺旋角在优化过程中的优选范围为[20,60]°。取螺旋角为45°，楔数为8，图7b所示为不同间隙膜厚下，动压承载力与楔深h1的关系曲线。当间隙膜厚一定时，动压承载力随楔深的增大先增大后减小，且能使动压承载力达到最大的楔深随间隙膜厚增大而呈增大的趋势。最终选定楔深的优选范围为[200,600]μm。取螺旋角为45°，楔深为200μm，图7c所示为不同间隙膜厚下动压承载力随楔数n的变化规律。当间隙膜厚一定时，随楔数的增多，动压承载力呈先增大后减小的趋势。最终选定楔数的优选范围为[6,14]且都为整数。故本优化模型设计变量为螺旋角β，楔深h1及楔数n，即：

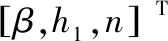
(15)

3.1.3 约束条件

液膜温度过高会对润滑油粘度及转台表面热变形造成较大的影响，本文约束转台平均温升不能超过10℃，故约束条件可表示为：

g(X)=ΔT-10≤0

(16)

故优化模型可表达为：

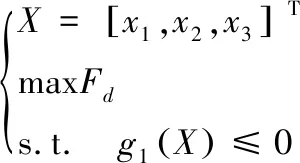
3.2 优化结果及变化规律

布谷鸟搜索算法中的关键参数包括种群规模N、切换概率Pa、步长缩放因子α和Lévy指数λ。综合考虑算法的可靠性和计算时间，选择种群规模N为25，切换概率Pa为0.25，步长缩放因子α为0.01，Lévy指数λ为1.5。在转台差动转速ω=30rpm，转台间隙h0=140μm的工况下，以螺旋楔形织构螺旋角β、楔深h1，楔数n为设计变量，得到以动压承载力为目标函数的优化问题的解为：最优螺旋角β=28.14°，最优楔深h1=380.77μm，最优楔数n=12。

为寻求最优解在不同工况下的变化规律，继续探究差动转速和液膜间隙厚度对最优解的影响。工作状态时，工作台与动环间差动转速范围为10～60r/min；考虑到转台摩擦表面粗糙度、润滑油的清洁度、端泄量等因素，间隙膜厚h0也应控制在合理范围，分别计算ω=[10, 20, 30, 40, 50]rpm，h0=140μm和ω=30rpm，h0= [100, 120, 140, 160, 180]μm的工况下最优解的变化情况，如表2、表3所示。

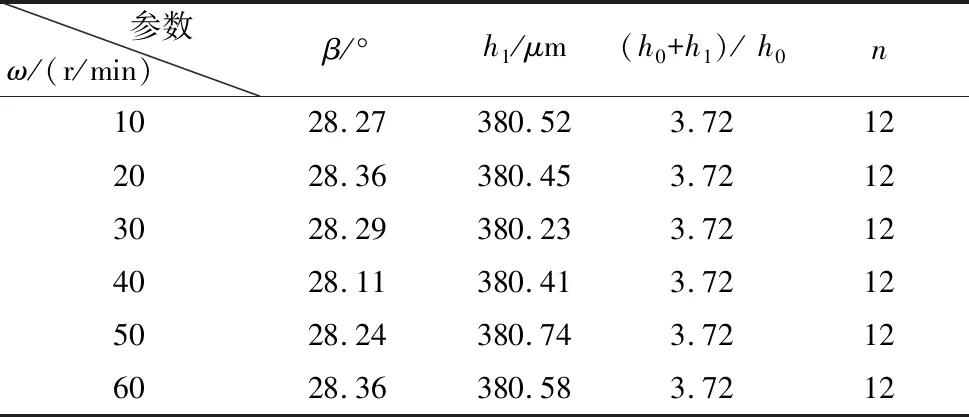
表2 不同转速下的最优解

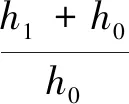
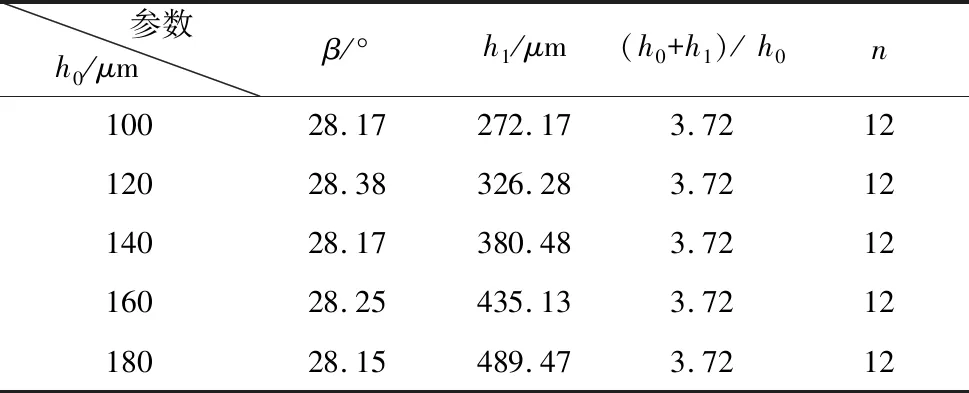
表3 不同液膜间隙下的最优解

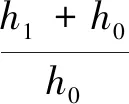
3.3 CFD仿真验证

为验证优化结果的可靠性，使用CFD软件ANSYS FLUENT仿真两种转速(30rpm/ 60rpm)下优化前后动压力分布及动压承载力，再与理论计算结果进行对比。使用ICEM CFD软件对油楔模型进行网格划分，采用混合(mixture)模型作为多相流模型，得到优化前后膜厚h0=140μm，转速分别为30rpm和60rpm的工况下动压区力分布如图8所示。

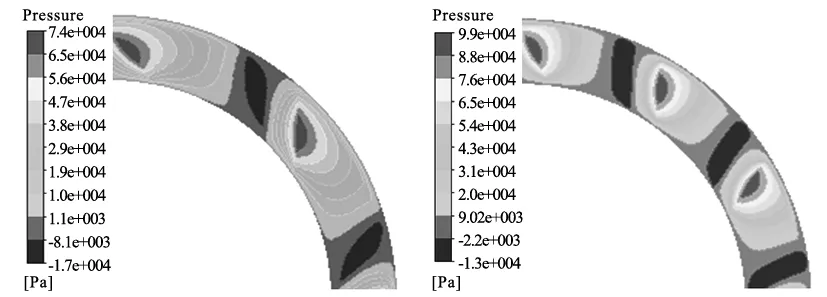
(a) 优化前;30rpm (b) 优化后;30rpm

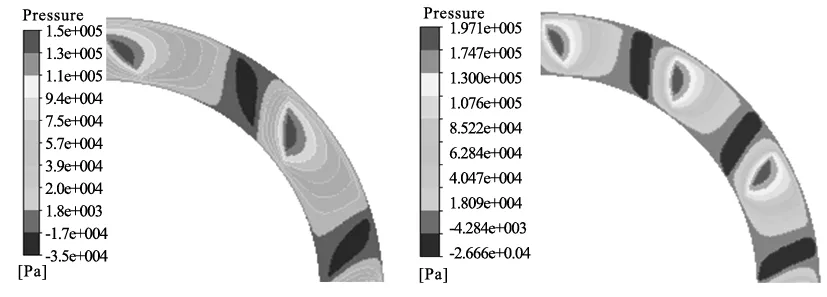
(c) 优化前;30rpm (d) 优化后;60rpm图8 优化前后动压分布CFD仿真结果

由图可见，转速为30rpm时，优化前油楔可提供的动压峰值约为0.074MPa，优化后动压峰值约为0.099MPa，提升约33.8%；转速为60rpm时，优化前压力峰值约为0.15MPa，优化后压力峰值约为0.20MPa，提升约33.3%。

优化前后CFD仿真及MATLAB理论计算得出的动压承载力对比如图9所示。

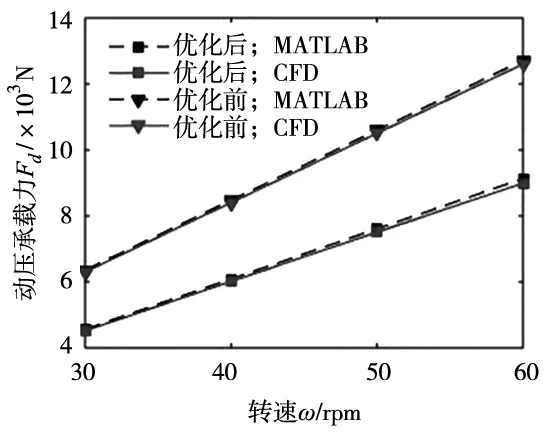
图9 CFD仿真与理论计算对比

由图可见，理论计算与CFD仿真结果契合良好，可以证明本文理论计算方法的正确性；通过对比优化前后螺旋楔形可提供的动压承载力，可以看出优化后的油楔动力学性能显著提高。

3.4 优化前后承载能力对比

转台工作阶段间隙膜厚范围约为100～160μm，故最优楔深选择范围可确定为[270,440]μm。取间隙油膜厚度为100～160μm，差动转速由30rpm调至60rpm，转台优化前及优化后(螺旋角为28°、楔数为12，楔深380μm)的结构参数下，摩擦副动压承载力、总承载力、动压泄漏流量及供油压力变化情况如图10所示。

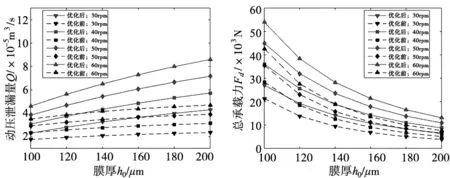
(a) 动压承载力 (b) 总承载力

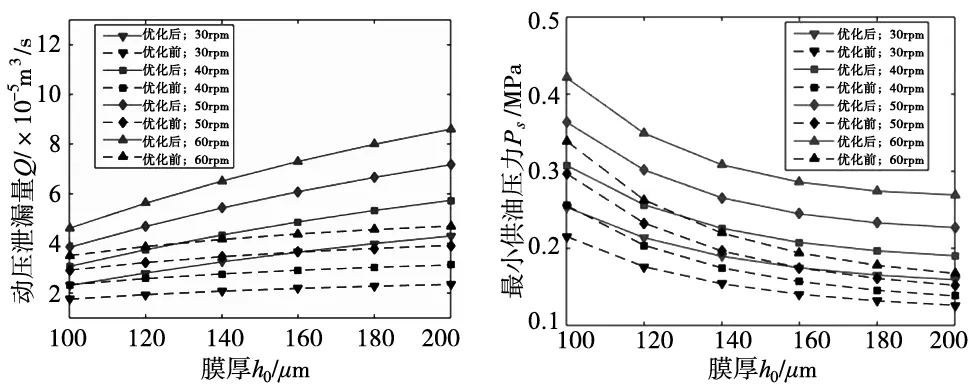
(c) 动压泄漏量 (d) 最小供油压力图10 优化前后性能对比

由图可得，在差动转速为30～60rpm时，优化后的摩擦副动压承载力、总承载力较优化前显著提升，回转工作台工作能力得到改善，同时动压泄漏量也较之前明显提高。根据以上现象可以看出优化结构动压泵出效应更强，同时加速润滑油流动可以更快地带走摩擦产生的热量，改善摩擦副内润滑环境。流量的提高会要求更高的供油压力，可能会需要更多的功耗。

4 结论

本文以一种新型动静压转台为研究对象，为提高其承载能力对螺旋油楔结构参数进行改进，得到以下结论。

(1)通过坐标变换，建立边界拟合坐标系下的螺旋楔形织构模型，并通过数值计算控制方程进一步获得液膜压力分布、承载力、动压泄漏量、平均温升等性能参数。并通过与CFD仿真结果的比较证明了计算方法的正确性。

(2)探究螺旋油楔几何参数对转台承载性能的影响，发现摩擦副中动压承载力随螺旋油楔螺旋角、楔深、楔数的增加均呈先增大后减小的趋势。建立以动压承载力为目标函数的优化设计模型，选择螺旋角、楔深、楔数为优化模型的设计变量并根据以上结论确定其优选范围。

(3)得到固定工况下使动压承载力达到最大的螺旋角、楔深和楔数组合，并探究最优解在不同工况下的变化规律。得到结论为：在任何工况下，最优解中螺旋角为28°，楔数为12个，并可以根据油楔进出口最优膜厚比3.72确定楔深。优化后的转台与优化前相比，动压泵出效应增强，动压承载力和总承载力显著提高；同时动压泄漏量增大，有利于改善润滑环境。