预裂裂纹对岩石试件应力分布及变形规律的影响

孙鼎杰 郭鹏飞

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.绍兴文理学院 岩石力学与地质灾害实验中心，浙江 绍兴 312000)

岩石材料具有不连续性、非均匀性和各向异性等特征，且岩石内部存在天然的缺陷，如预裂裂纹、节理、层理等，这些均严重影响了岩石的强度.其中，预裂裂纹对岩石强度的影响较为显著.随着我国经济的迅速发展，对资源的需求日趋增大，在资源开采的过程中许多问题随之而来.例如，当岩体内部结构发育较差时，在地应力作用下岩体容易产生变形，且在变形的过程中伴随着裂纹的扩展、延伸及贯通，使岩体产生断裂破坏，从而造成大量的财产损失和人员伤亡.由裂纹导致岩石破坏的内在原因，即在裂纹扩展变形的过程中岩体内应力会重新分布，使新的区域应力达到临界断裂应力，从而使岩石产生断裂破坏.研究预裂裂纹岩体的变形和裂纹周围应力分布规律，不仅会对岩体断裂力学问题有更进一步的认识，而且也将对岩石力学与工程理论有深入的了解，研究成果将对岩体灾害防治有理论和现实意义.

随着岩石工程项目的开展，国内外学者对预裂裂纹岩体进行了多方面的研究，并取得了丰硕的成果.Inglis早在1913年通过对带有椭圆通孔平板的拉伸应力分布进行研究和计算，证明了应力集中现象的存在[1]；Griffith在1920年指出，预裂裂纹的存在对脆性材料稳定性的影响很大、对材料的稳定性影响显著，从而在理论上有很大的突破[2]；Lajtai研究了含预制裂纹的石膏试件在单轴压缩条件下的脆性破坏过程，给出了裂纹断裂扩展的演化过程[3]；Chua和Wong等人使用类砂岩模拟材料，研究了含不同角度分布的预置裂纹的贯通机制，对岩桥贯通失效机制进行了一系列的研究[4]；陈卫中与李术才等研究了闭合裂纹在单轴和双轴荷载作用下，预裂裂纹扩展、贯通的规律[5]；Tang和Kou采用RDPA2D软件，从数值分析角度研究了硬岩中裂纹的扩展及贯通规律[6]；唐谦与李云安采用PFC颗粒流数值模拟方法，预设了单预裂裂纹岩石在双向压缩状态下裂纹扩展的过程[7].

为了研究预裂裂纹岩石材料的变形及其破坏过程，研究人员运用了各种先进的技术手段，但是他们主要偏重于研究有角度的单裂纹或多裂纹扩展以及在不同围压下的裂纹扩展.本文基于上述研究结果，采用FLAC3D数值仿真软件，对相同正压力、剪切力但不同长度的竖直预裂裂纹岩样进行模拟剪切实验，结合断裂力学理论，探究不同预裂裂纹长度下岩石的应力分布及变形规律，为岩体相关工程施工提供参考.

1 岩石预裂裂纹强度理论

1.1 Griffith断裂理论

Griffith对钢和玻璃等脆性材料进行试验研究，并于1920年提出断裂强度理论，岩石断裂理论也起源于此.Griffith断裂理论为岩体断裂破坏机理研究奠定了基础.Griffith认为，材料断裂的起因是由于材料内部存在微小裂纹，在受到力的作用时在裂纹的尖端产生应力集中现象，材料中的众多微小裂纹相互贯通从而使材料产生断裂破坏.Griffith考虑了如图1所示的受拉平板，认为预裂裂纹失稳扩展的临界条件，是预裂裂纹扩展时所需要的表面能正好与预裂裂纹扩展时系统释放的弹性应变能相抵[8].裂纹扩展满足的条件为：

(1.1)

式中：σc为临界应力；a为预裂裂纹的半长；γ为形成单位面积新表面所需要的表面能.

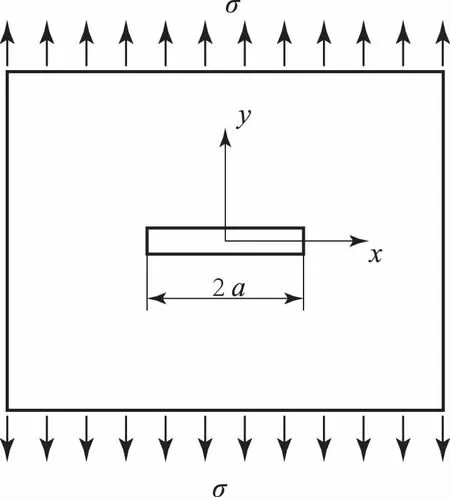
图1Griffith断裂理论示意图

其后，Griffith把强度理论用于压缩试验裂纹扩展研究，在不考虑摩擦对压缩下闭合裂纹的影响，以及假定椭圆裂纹将从最大拉应力集中点开始向外扩展的情况下，获得了双向压缩下裂纹扩展准则，即所谓的Griffith强度准则[9]：

(1.2)

式中：σ1为正压力；σ3为侧压力；σt为脆性材料的单轴抗压强度.

1.2 Griffith的能量平衡理论[10]

Griffith在Inglis得到的裂纹周围应变能密度的基础上，设置板厚为单位1，并假定为平面应力的情况下，得到的弹性势能公式为：

(1.3)

式中E为杨氏弹性模量.由于裂纹的出现，其增加的表面能为：

S=4aΓ，

(1.4)

其中，Γ为单位面积的表面能.Griffith认为，当裂纹尖端部扩展一小段长度da(裂纹长度从2a→2a+da)时，弹性势能的释放率dWc/da如果大于或等于表面能的增加率dS/da，则裂纹处于不稳定状态，必定会进一步扩展，因此得到裂纹扩展的条件为：

(1.5)

将式(1.3)和式(1.4)代入式(1.5)中，得到临界应力σg为：

(1.6)

式中E和Γ是材料的常数.式(1.6)与其他判断临界应力公式的最大区别在于，σg不仅与材料性质有关，而且与裂纹长度有密切关系.

1.3 裂纹周围的应力和位移

为了进行裂纹问题的应力分析，首先要确定裂纹的类型.根据裂纹尖端的受力形式以及断裂特征，裂纹可分为3种基本的类型(如图2)，分别为Ⅰ型(张开型)、Ⅱ型(滑开型)和Ⅲ型(撕开型)[11].

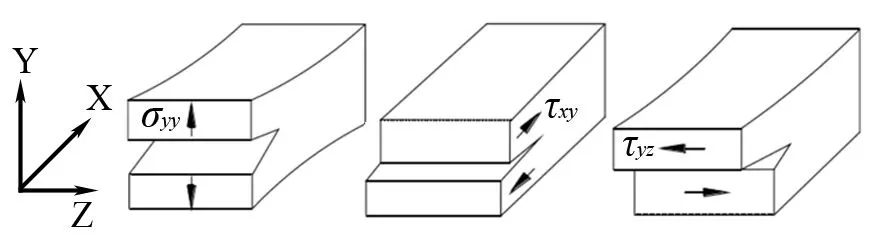
Ⅰ型 Ⅱ型 Ⅲ型

图2裂纹的3种基本类型

岩石试件在承受竖直和水平荷载情况下，裂纹以滑开裂纹的形式存在，因此本文研究的是Ⅱ型裂纹.当裂纹尖端承受Ⅱ型应力作用时，裂纹将发生滑开型断裂，其裂纹尖端在极坐标中的应力分量表达式为[12]：

(1.7)

式中：KⅡ表示Ⅱ型裂纹的应力强度因子；σrr、σθθ和τrθ分别为裂纹尖端径向应力、周向应力和剪切应力；θ为裂纹偏离角度；r为裂纹外某点与裂纹尖端的距离.

裂纹尖端位移场分量为[13]：

(1.8)

其中：ur为裂纹尖端在X方向产生的位移；uθ为裂纹尖端在Z方向产生的位移；k为岩石材料常数.

2 FLAC3D数值模拟

2.1 FLAC3D软件简介

FLAC(Fast lagrangian Analysis of Continua)是由美国ITASCA公司研发的连续介质力学分析软件.FLAC源于流体力学，其基本原理类似于离散元法，最早由Willkins应用于固体力学领域，目前已经成为岩石力学最主要的计算方法之一.FLAC3D所采用的显式拉格朗日算法和混合-离散分区技术，能够非常准确地模拟材料的塑性破坏和流动.FLAD3D不仅可以处理一些大变形的几何非线性问题，模拟岩体沿某一弱面产生的滑移变形,也可以处理诸多有限元程序难以解决的复杂工程问题.

在算法上,FLAC3D相对于有限元软件有以下几个优点：

(1)采用“混合离散法”模拟材料的塑性破坏和塑性流动，这种方法相对于有限元方法所采用的“离散集成法”在结果上更加合理[14].

(2)即使问题的本质是静力问题，FLAC3D也会采用动态的运动方程进行求解，这就使得其在模拟物理学中的不稳定过程时不存在数值上的障碍.

(3)采用显式差分法求解微分方程.对于显式法来说，线性本构关系与非线性本构关系在算法上并无差别，对于已知应变增量，可以快速准确地求出应力增量，并得到平衡力[15].可以追踪系统的演化过程，不需要储存刚度矩阵，所需内存较小，可以用较小的内存模拟出大量的单元.

2.2 方案的设计和参数的选取

为了研究不同长度的竖直预裂裂纹岩石在剪切实验过程中的位移和应力规律，本文采用FLAC3D数值仿真软件进行模拟试验，以阐明预裂岩石破坏的力学机制.数值模拟采用的单元体尺寸为150 mm×150 mm×150 mm，分别在6个不同的竖直预裂裂纹长度(0 mm、20 mm、50 mm、80 mm、110 mm和140 mm)条件下进行岩块的剪切试验，数值模拟参数见表1，主要监测指标为其变形和应力.

表1 数值模拟参数

序号裂纹长度/mm正应力/Pa剪应力/Pa102×1042×1042202×1042×1043502×1042×1044802×1042×10451102×1042×10461402×1042×104

由于FLAC3D软件模拟时需要定义岩石单元体微观参数，而在现实中只能得到岩石的宏观参数，因此需要通过计算得到岩石单元体的微观参数.岩石的宏观力学参数见表2.利用以下经验公式及岩石的宏观参数公式[16]，可计算模拟时所需的岩石微观参数.岩石体积模量K的计算公式为：

(2.1)

岩石剪切模量G的计算公式为：

(2.2)

式(2.1)和式(2.2)中的E为岩石的弹性模量，μ为岩石的泊松比.

计算所得单元体的微观力学参数见表3.

2.3 模型生成及荷载施加

首先建立单元体.模型试样尺寸大小为150 mm×150 mm×150 mm，按照比例划分网格.在单元格生成后，根据预设裂纹的空间坐标将相应位置的单元格删除，从而生成含预裂裂纹的试样.预裂裂纹竖直且裂纹在试样的中轴线上，宽为2 mm，使用表2参数赋予模型材料属性.如图3所示，设置约束边界条件及施加应力：固定模型沿Y方向所有的面，在Z方向左侧面施加均布荷载，右侧面固定；在X方向裂纹右侧的顶面上施加均布荷载；通过Fish函数控制正应力和剪应力保持不变.建模完成后，在6个不同裂纹长度(0 mm、20 mm、50 mm、80 mm、110 mm和140 mm)条件下进行剪切试验，通过试验探究在不同预裂裂纹长度的影响下，岩石的应力分布及变形规律.

表2 岩石试验宏观力学参数

项 目 数 值 密 度/(kg·m-3)2.55 单轴压缩模量/GPa20.00 单轴抗压强度/MPa45.00 抗拉强度/MPa19.60 泊松比 μ0.20

表3 单元体的微观力学参数

项 目 数 值 体积模量/GPa11 剪切模量/GPa8 内聚力/MPa6.7 剪胀角/(°)15 抗拉强度/MPa19.60

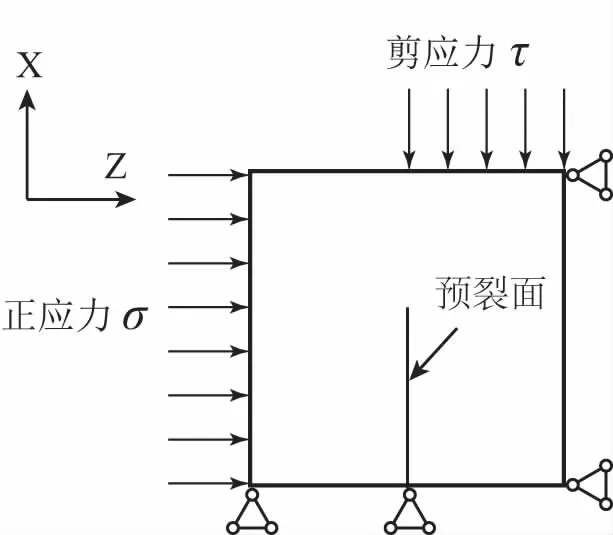
图3 模拟剪切试验示意图

3 模拟结果

3.1 变形

不同预裂裂纹长度下岩块达到平衡时X方向上的变形如图4所示.由图4可以看出：

(1)当预裂裂纹长度不超过80 mm时，岩石在X方向上产生的位移不均匀，对裂纹右侧岩体有明显的影响；当预裂裂纹长度大于80 mm时，岩石在X方向上产生的位移逐渐均匀，对裂纹右侧的岩体几乎没有影响.

(2)随着X方向的预裂裂纹长度不断增大，裂纹两侧岩块的相对位移也在增大，更容易使相对位移达到临界位移条件而产生破坏.

3.2 应力分布

不同预裂裂纹长度下岩块达到平衡时X方向上的应力分布如图5所示.由图5可以看出：

(1)随着裂纹长度的增大，正应力和剪应力的合力在裂纹周围的影响都集中在裂纹端部，合力影响范围在逐渐变小，裂纹端部应力集中程度增大.

(2)随着裂纹长度的增大，X方向的应力越来越大，裂纹尖端的应力集中程度也越来越高，岩石会达到临界破坏条件而产生破坏.

4 结论

本文利用FLAC3D数值模拟软件，分别对预裂裂纹长度为0 mm、20 mm、50 mm、80 mm、110 mm和140 mm的预裂岩石开展数值模拟(图3)，研究剪切条件下的岩石变形及其应力分布规律(图4和图5)，通过模拟实验得到如下结论：

图4 不同预裂裂纹长度下X方向的位移

(1)预裂裂纹的长度对岩石X方向的变形有显著影响.当预裂裂纹长度在0～50 mm之间时，预裂裂纹左侧岩石的位移分布不均匀，对岩石右侧的影响较大；当预裂裂纹长度在80 mm～110 mm之间时，预裂裂纹左侧岩石的位移分布趋于均匀，对右侧岩石几乎没有影响；当达到140 mm时，左侧岩石的位移分布更加均匀.

(2)预裂裂纹的长度对岩石X方向的应力分布有显著的影响.当预裂裂纹长度在0～50 mm之间时，外力在预裂裂纹周围较大范围内产生影响；当预裂裂纹长度在80～110 mm之间时，外力的影响范围逐渐减小，而在预裂裂纹端部产生较大的影响，应力集中程度越来越高；当达到140 mm时，应力集中程度更高.

(3)通过分析位移图和应力图中的数据发现，随着预裂裂纹长度的增加，预裂裂纹左侧岩石的位移更加均匀，裂纹尖端应力更大，岩石将会沿裂纹尖端处发生断裂破坏，且两侧岩石相互扰动影响较小.

(4)综合各方面因素并考虑岩块X方向的位移和应力分布规律可知，当预裂裂纹达到岩块长度的53%～73%时为岩石的最佳预裂裂纹长度，这时预裂裂纹两侧岩体的相互扰动影响最小，这一点具有重要的工程实际意义.

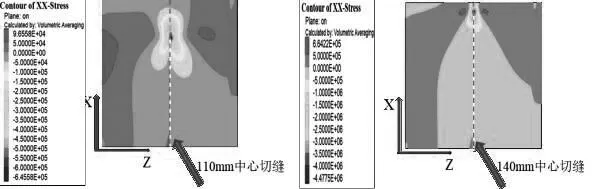
图5 不同预裂裂纹长度下X方向的应力