聚焦主题精选学材，由浅及深渐次展开——以“线段之间数量关系”专题复习课为例

☉江苏省海门市能仁中学 陆新锋

几何综合复习阶段，常常有一类探究三条线段之间数量关系的综合题，这类问题学生往往找不准求解方向，导致思路受阻.为了帮助学生做好复习，我们围绕专题开展了精准复习，起到了一定的效果，本文梳理这节专题复习课的教学流程，并给出教后思考，供研讨.

一、“线段之间数量关系”专题复习课

教学环节（一） 经典问题，回顾性质

经典问题1：如图1，等边三角形ABC中，点P是边BC上一点，连接AP，将线段PA绕点P顺时针旋转60°到PQ位置，连接CQ，求证PC+CQ=AC.

教学预设：可以在AC上取一点H，构造等边三角形CQH，进一步证明△AQH △PQC，可以构造AH=PC，HQ=QC=HC，于是AC=AH+HC=PC+CQ.问题获证.证后还应引导学生“成果扩大”，认识这个问题还能得到如下一些结论或性质，比如，连接AQ，△APQ是等边三角形，CQ是△ABC的一个外角平分线，点Q一定在该外角的平分线上，等等.

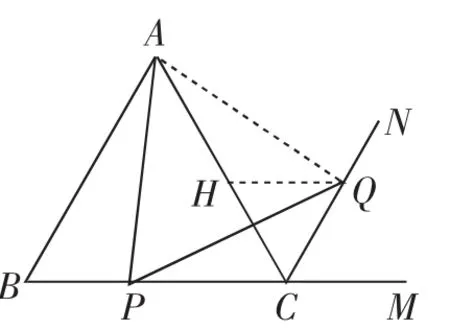
图1

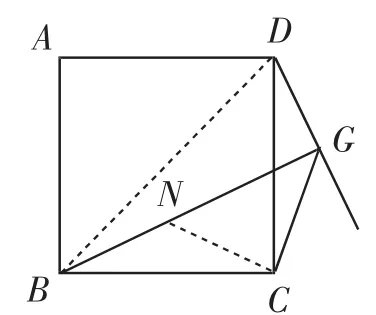
图2

经典问题2：如图2，过正方形ABCD的顶点引一条射线DG，过点B作BG⊥DG，垂足为点G，连接CG.探究DG、CG、BG的数量关系.

教学预设：由∠BCD、∠BGD都是直角，可确认B、C、G、D四点共圆，于是∠BGC=45°，利用这个特殊角度构造等腰直角三角形CGN，进一步证明△BCN △CDG，可以沟通.从而有.

教学环节（二） 例题探究，学会转化

例1（北京人大附中2018年12月初三考卷）如图3，∠MON=α（0°＜α＜90°），A为OM上一点（不与O重合），点A关于直线ON的对称点为B，AB与ON交于点C，P为直线ON上一点（不与O、C重合），将射线PB绕点P顺时针旋转β角，其中2α+β=180°，所得到的射线与直线OM交于点Q.

这个问题中，点P的位置和角α的大小都不确定，在这里我们仅研究两种特殊情况，更一般的情况留给同学们深入探索.

（1）如图3，当α=45°时，β=90°，若点P在线段OC的延长线上，

①依题意补全图形；

②求∠PQA-∠PBA的值.

（2）如图4，当α=60°，点P在线段CO的延长线上时，用等式表示线段OC、OP、AQ之间的数量关系，并证明.

教学预设：先安排补全图形，如图5，探究∠PQA-∠PBA的值有两种典型思路.思路之一，将∠PBC等量代换到∠QPO，然后就能利用△POQ的外角性质得出∠PQA-∠QPO的值为∠MON（45°）；思路之二，连接OB，确认四边形OBPQ是对角互补的四边形，则∠PQA=∠PBO，于是∠PQA-∠QPO转化为∠PBO-∠QPO，再转化为∠CBO（45°）.

在第（2）问中，当α=60°时，可得β=60°，如图6，连接OB，可以发现图形中有一个基本图形，引导学生利用开课阶段复习的“经典问题1”，可在OQ上取一点H，构造等边三角形OPH，从而得到OQ=OB+OP，进一步利用OB=OA=2OC，可得AQ=4OC+OP.

例2（北京十一学校2018年12月初三考卷）如图7，在△ABC中，∠ACB=90°，∠CAB=α，点D为AC的延长线上一点，连接BD，作AE⊥BD于点E，将射线AE绕点A逆时针旋转α后，所得的射线与BD的延长线交于点F，连接CE.

（1）①依题意补全图形；

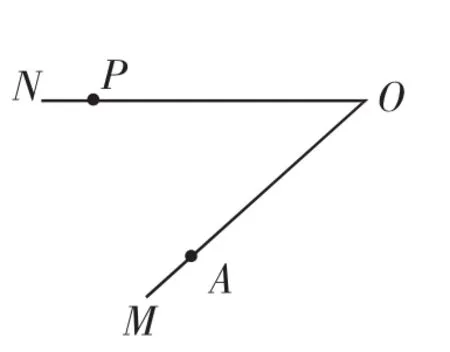
图3

图4

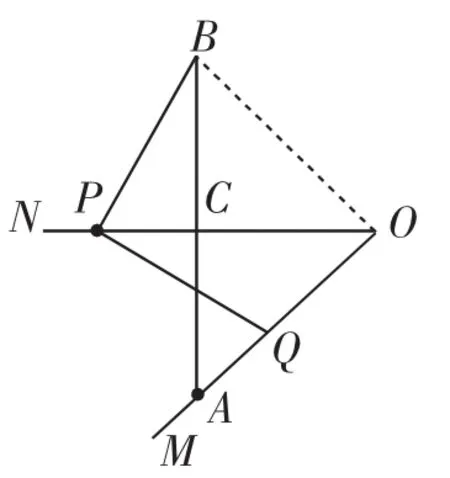
图5

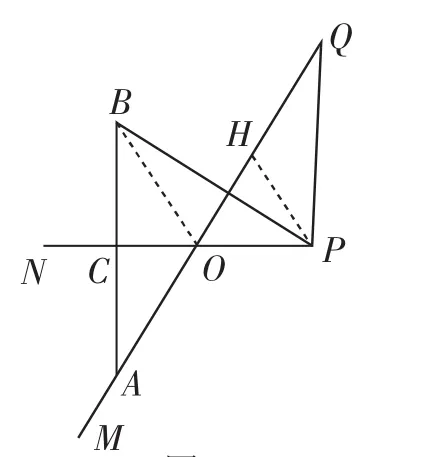
图6

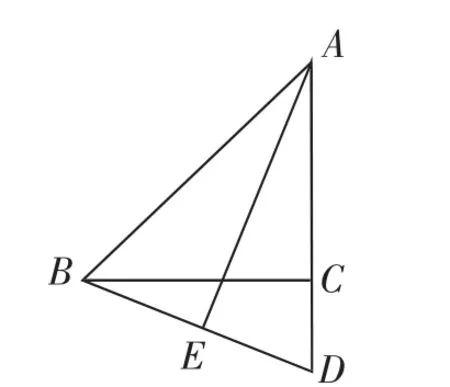
图7

②当∠CAB=α时，用含α的代数式表示∠AEC为_______.

（2）当AC=BC时，用等式表示线段AF、CE、BE之间的数量关系，并证明.

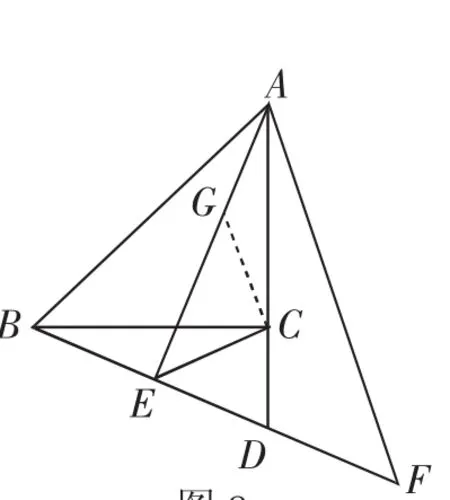
图8

教学预设：先补全图形，如图8，容易确认点A、B、E、C共圆，于是∠AEC=∠ABC，而∠ABC=90°-α，则第（1）问获解.第（2）问中的三条线段比较“分散”，先确定，接下来集中精力思考BE、AE、CE三条线段的数量关系，可联想到上面的“经典问题2”，构造等腰直角三角形CEG，可得进一步可代换得

教学环节（三） 继续前进，变式拓展

例3（北京交大附中2018年10月）如图9，Rt△ABC中，∠ACB=90°，AC=BC，过点C在△ABC外作射线CE，且∠BCE小于45°，点B关于CE的对称点为D，连接AD、BD、CD，其中AD、BD分别交射线CE于点M、N.你发现线段AM与CN之间有怎样的数量关系？证明你的发现.

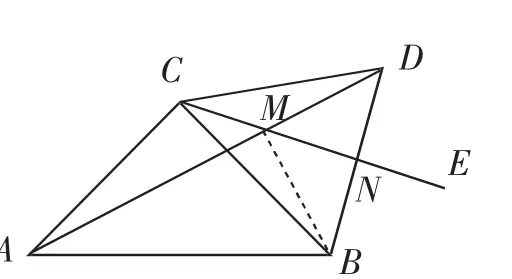
图9

教学预设：连接BM，学生需要先证出BM⊥AD，进而确认△ABM是直角三角形，△BMD是等腰直角三角形.这样由勾股定理可得AB2=AM2+BM2，BM2=2BN2，BC2=BN2+CN2，AB2=2BC2，这样就可代换得AM2+BM2=2BN2+2CN2，于是，AM2+BM2=BM2+2CN2，于是AM2=2CN2，即

教学环节（四） 课堂小结，拓展思考

围绕本课所学，安排学生小组交流学习了哪些新的内容，对几条线段之间数量关系的探究有了哪些新的认识或理解，各小组推荐两人到讲台前向大家汇报交流，谈本课所学的收获.然后出示如下拓展题.

拓展题：如图10，矩形ABCD中，点E、F分别在边BC、CD上，当∠EAF=∠EFC=45°时，分析线段BE、EF、DF之间的数量关系.

图10

图11

图12

教学预设：学生可能会有困难，这里可先出示铺垫式问题，如图11，等腰直角三角形ABC中，∠ECF=45°，这是一个经典问题，学生应该能想起该图的一个经典结论于是可以想到构造图12这样的等腰直角三角形AGH，问题获得有效转化，相继发现可代换得

二、教后思考

1.专题复习课需要聚焦主题与精选学材

我们知道，专题复习课在选题上呈现出以题型来选题，或者以知识点来选题的备课价值观，这种选题的指导思路之下，很多习题虽然题型相同、知识点相近，但是解题策略、思路方法大相径庭，无法做到聚焦主题.这就要求我们在研发、打磨专题复习课时，把聚焦主题作为第一追求，在此基础上精选学材，学材的来源可以是教材上例题、习题、拓展题，也可是各地中考题中的相关素材，但这些素材选定之后，并不能简单地直接拿来，还需要进一步整合、删减、改编或拓展生长.本课例就是由两道北京名校最新考题出发，“思前想后”→整合素材→生成学材.

2.专题复习课需要由浅及深与渐次推进

专题复习课在选定素材、生成学材之后，还需要由浅及深、渐次呈现这些学材内容.在上文课例中，我们选择的是从两个“经典问题”（学生在八年级就已对相关练习进行过训练）出发，先复习确认已有性质或求解经验，再依次给出两道几何综合题，先由学生独立探究出三条线段之间的数量关系，并且小结在黑板上，为后续探究问题提供转化方向.本课主要教学用时花在例1、例2的研究上，这两道习题都需要先补全图形，再构造辅助线转化为熟悉的“经典问题”.教学过程中，要注意向学生渗透和传递“回到经典问题去解题”的解题与探索方法.此外，专题复习课在预设各个教学环节中的较难习题时，还应注意铺垫设问与适当“留白”相结合，既让大多数学生在铺垫设问下体验到挑战难题的自信，又让少数优秀学生能在适度留白式的探究中体验到攻克较难习题的乐趣.在上文课例中的经典问题与例1、例2的探究中可体现出铺垫设问的教学价值；而在最后环节的拓展题中又是“留白”式的教学安排，只适合少数优秀学生独立探究、实现问题转化，教师在教学组织时也可根据学情相机进行适当的“教学干预”（提供帮助或铺垫式问题）.