基于模态回归的半参数部分线性模型的稳健估计
2019-05-18高佳佳何晓霞
高佳佳,何晓霞
(武汉科技大学理学院,湖北 武汉,430065)
半参数回归模型结合了线性回归和非线性回归模型,既包含参数分量又包含非参数分量。参数分量用于对确定性因素进行分析,而非参数部分能够对随机干扰因素进行刻画。与线性模型相比,半参数回归模型更具灵活性,能更好地解释每一个变量的效应,因此,其在理论研究和实际应用中都有重要意义。
针对具体问题,通常假设数据来自于某一参数模型或非参数模型,然而许多实际问题并没有那么简单。例如,影响考察对象(指标Y)的因素(解释变量)可分为两部分,即(X1,X2,…,Xp)及T,根据经验或历史资料可以认为因素 (X1,X2,…,Xp) 是主要的,Y与(X1,X2,…,Xp)线性相关,而T则是某种干扰因素(或看作为协变量),它同Y的关系是完全未知的,而且没有理由将其纳入误差项,如果用非参数回归加以处理,则会丢失太多的信息,若采用线性回归方法,一般拟合情况很差,这种情况下就可采用半参数回归模型。
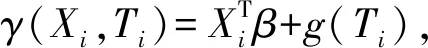
为了解决异常值的问题,研究人员开始考虑稳健估计方法。Zhu等[7]提出针对大维度协变量的稳健估计方法。Yao等[8]基于局部模态回归建立了一种用于非参数模型的估计方法,能根据观测数据自动调整参数。该估计方法不仅在数据集包含异常值或者误差分布重尾的时候具有稳健性,还能满足数据集没有异常值或者误差分布为正态分布时的渐进最小方差性。Zhao等[9]基于模态回归研究了半参数变系数部分线性模型。本文拟运用模态回归来研究半参数部分线性模型中参数和非参数部分的估计问题,探讨估计量的大样本性质。
1 模型描述
半参数部分线性模型的一般形式可以表示为
(1)
式中:Yi为响应变量;Xi=(xi1,xi2,…,xip)T;β=(β1,β2,…,βp)T为待估未知参数;(Xi,Ti)是独立同分布的随机设计或固定非随机设计点列;εi是独立同分布的随机误差项;g(·)是定义在R上的未知光滑函数。
2 稳健估计方法
2.1 模态回归
作为衡量指标,均值、中值和模是误差分布的3个重要数值特征,其中,中值和模在处理异常值上具有同等的稳健性。另外,模态回归对于大多数的数据可以提供有意义的点预测,并且对于相同长度的区间估计,当误差分布不规则时,模态回归相比于其他方法能预测更大的范围,同时预测结果更有意义。
(2)
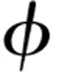
2.2 估计方法
假设(Xi,Ti)i=1,…,n是模型(1)的独立同分布样本。由于g(·)是未知的非参数函数,在文献[8]中采用局部多项式来近似g(·)。对于半参数模型,局部多项式估计有两个缺点:①β是一个全局参数,为了得到它的最优相合估计,需要采用两步估计法;②局部多项式估计的计算量非常大,尤其是在高维模型中。
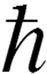

(3)
3 估计量的性质
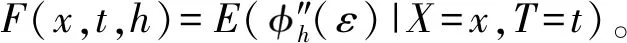
(C1) 指标变量T具有有界支撑Ω,其密度函数fT(·)为正,并且有连续的二阶导数。不失一般性,这里假设Ω=[0,1]。
(C2) 函数g(·)是区间[0,1]上r阶连续可微的函数,其中r>2。
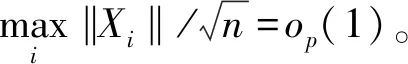
(C4) 令t1,…,tK为[0,1]区间的内部节点,t0=0,tK+1=1,ξi=ti-ti-1,ξ=max{ξi},存在常数C0使得
(C5)F(x,t,h)关于(x,t)连续。
(C6) 对于任意的h>0,有F(x,t,h)<0。

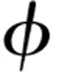
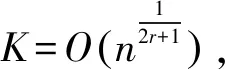
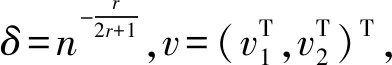
(4)
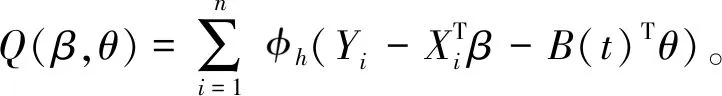
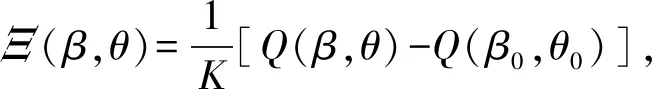
Ξ(β,θ)=
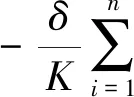
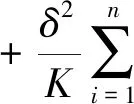
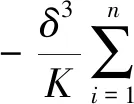
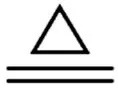
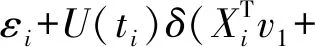
针对I1进行泰勒展开,有

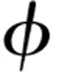
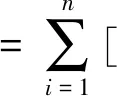
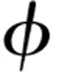
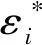
结合条件(C4)、(C7)和‖U(ti)‖=O(K-r),可以得到

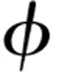
=Op(nK-r‖v‖)
(5)
因此I1=Op(nδK-(r+1)‖v‖)=Op(nδ2K-1‖v‖)。
对于I2,可以证明
I2=E[F(X,T,h)]Op(nK-1δ2‖v‖2)
(6)
因此,若选择足够大的常数C,则I2可通过‖v‖=C控制I1。
同样可以证明
I3=Op(nK-1δ3‖v‖3)
(7)
当n→的时候,有δ→0,因此δ‖v‖→0,从而有I3=op(I2)。故I2通过‖v‖=C控制I3。
因为I1、I2、I3均可以通过‖v‖=C控制,并且由条件(C6)知F(x,t,h)<0,所以通过选择足够大的常数C,有Ξ(β,θ)<0,从而有Q(β,θ)
因此存在一个局部最大化,使得
(8)
以上为定理1中结论(I)的证明,接下来证明结论(II)。
由于
4 带宽选择方法和估计算法
4.1 带宽选择
不失一般性,基于式(3),假设误差变量与Xi、Ti是独立的,并且类似于文献[12]中给出的最小二乘B样条估计(LSB)的渐进方差,这里给出BSMR估计量的渐进方差的比率:

(9)
可通过下式来选择h:
hopt=argminhr(h)=argminhG(h)F-2(h)
(10)
由式(10)可以知道,hopt仅由ε的条件误差分布来决定。
需要指出的是,根据r(h)的表达式:当h>0的时候,如果误差服从标准正态分布,infhr(h)=1;如果不考虑误差分布,infhr(h)≤1。因此,BSMR方法要优于或至少不劣于LSB方法,尤其是当误差分布有重尾或者大方差的时候,BSMR的性能要比LSB的性能好很多。
在实际应用中,若不知道误差分布,则得不到G(h)和F(h)。通常用下式来估计G(h)和F(h):
(11)
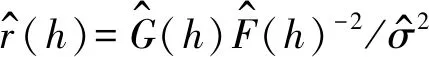
4.2 估计算法
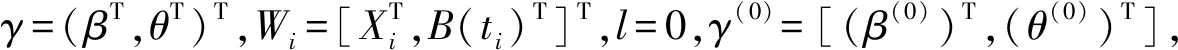
步骤1(E-step)通过下式更新π(i/θ(l)):
π(i/θ(l))=
i=1,2,…,n
步骤2(M-step)更新γ:
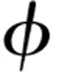
=(WTZW)-1WTZY,
其中,W=(W1,W2,…,Wn),Z=diag(π(1/γ(l)),…,π(n/γ(l))),Y=(y1,y2,…,yn)。

由于该算法的收敛值可能会依赖于初始值,并且不能保证EM算法可以收敛到全局最优解,因此需要对不同的初始值进行计算,并从中选取局部最优解。
另外,对于以上的估计过程,需要确定最优的节点数K,本文选取最大化交叉验证函数的解作为最优节点数,即
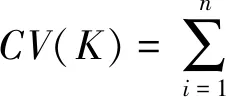
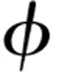
(12)

5 数值模拟和实例验证
5.1 蒙特卡洛模拟

对于非参数部分,使用均方误的平方根(square root of average square errors, RASE)指标来评价估计结果:
(13)
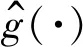
用文献[11]中定义的广义均方误(generalized mean square error, GMSE)来评价参数部分的估计结果:
(14)
数值模拟结果如表1所示,为了检验BSMR估计量的优效性和稳健性,表中还列出最小二乘B样条估计(LSB)[12]的结果进行对比分析。
从表1中可以看出,对于参数部分的估计,LSB和BSMR的估计误差都很小,性能比较接近,而且随着样本量的增加,两种估计的结果都会逐渐变好;对于非参数部分,当误差服从正态分布或者t分布时,BSMR估计误差比LSB的小很多,当误差服从混合正态分布时,BSMR的估计结果也好于LSB,但是差距不是特别明显。总的来看,BSMR估计要优于LSB估计。
5.2 实例分析
下面通过实例来验证BSMR估计方法的可行性。采用Nierenbrg等[16]收集的血浆中β胡萝卜素的水平数据,该数据集有315个观测值,本文研究血浆中β胡萝卜素的水平与下列因素的关系:年龄,性别,吸烟状况,克托莱指数,维生素服用情况,食物热量(卡路里),脂肪、膳食纤维、酒精饮料和胆固醇的摄入量。
应用模型(1)进行分析,其中T为年龄,协变量吸烟状况和维生素服用情况是分类变量,重新将它们设置为虚拟变量;将以上的虚拟变量和离散变量(性别)以及酒精饮料摄入量作为参数部分的协变量。将年龄指标T归一化处理。

表2给出了模型的系数以及参数估计的标准差。由表2可见,BMSR的MAPE值比LSB的MAPE值小,即BSMR 的拟合效果优于LSB,再次验证了本文方法的可行性及有效性。
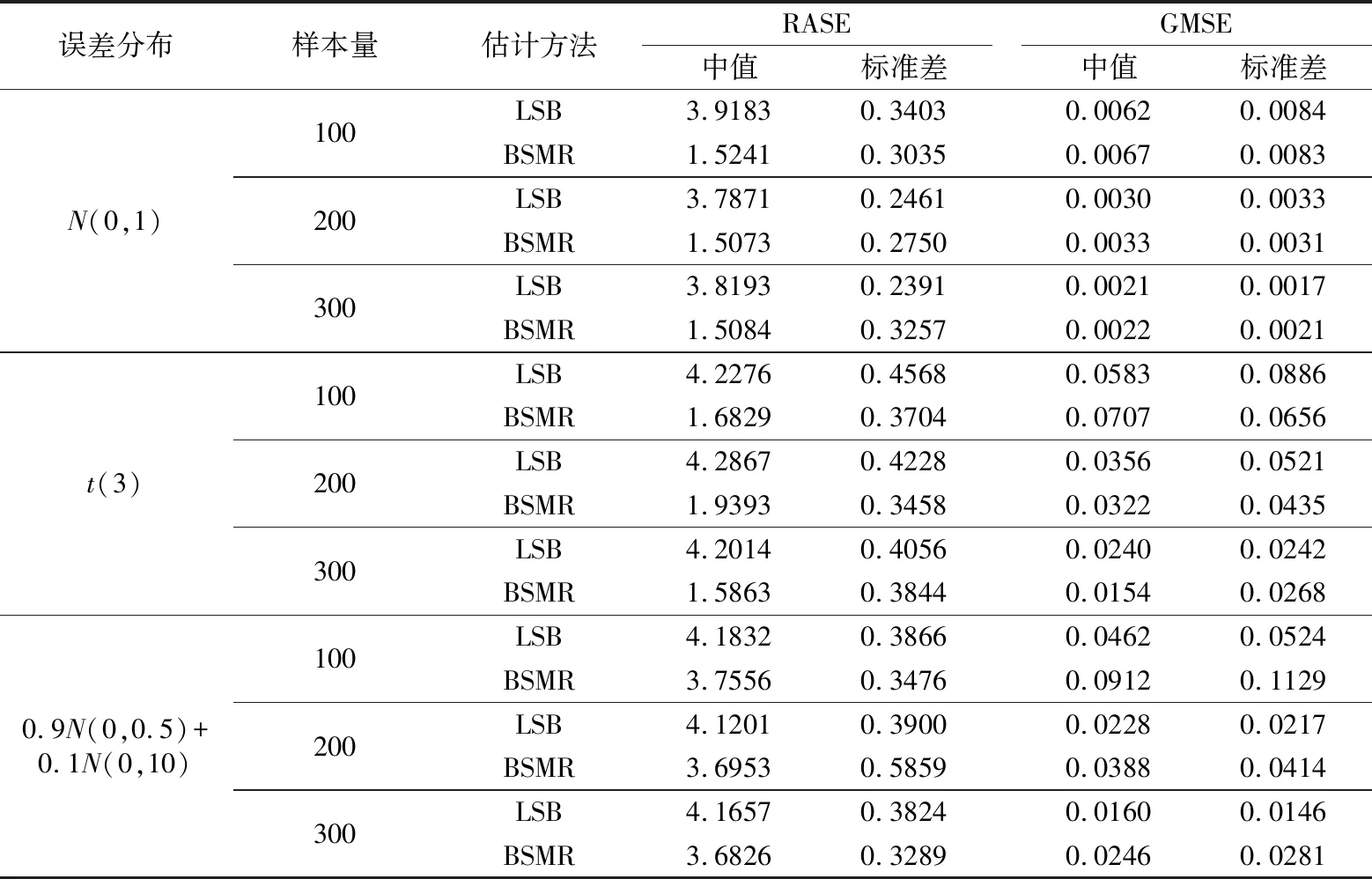
表1 不同误差分布下的模拟结果
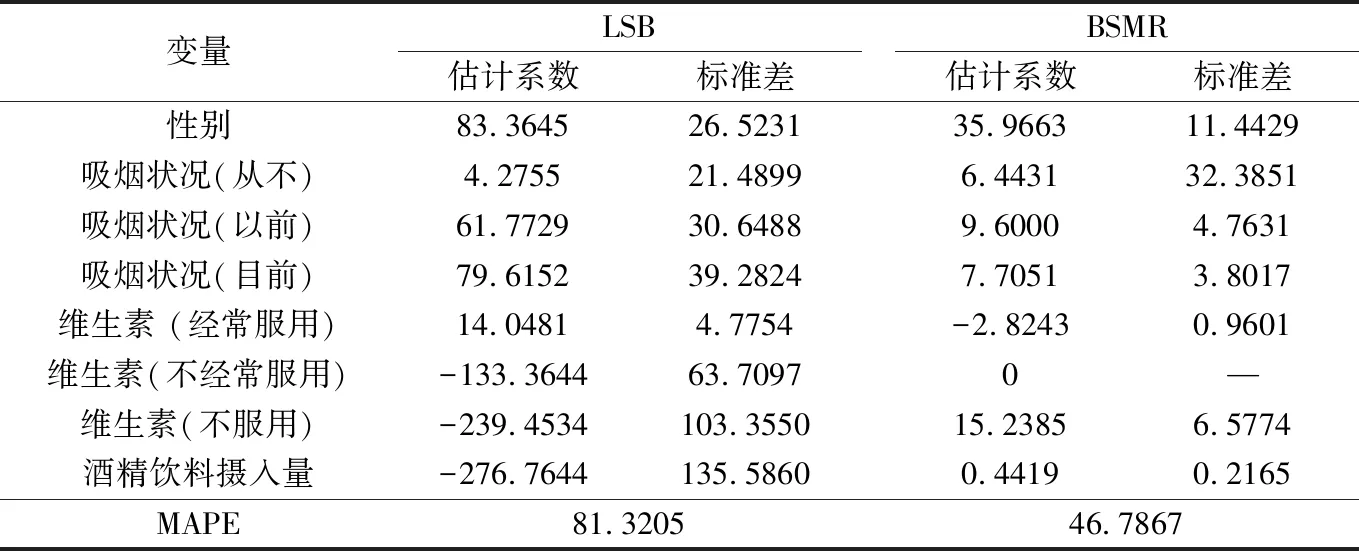
表2 参数估计值及其MAPE
