一种改进的主成分分析特征抽取算法：YJ-MICPCA

谢昆明，罗幼喜

(湖北工业大学理学院，湖北 武汉，430068)

随着现代信息技术的发展，维度较高的数据量与日俱增，其中包含的噪声信息也会增多，数据特征之间往往存在着一定的相关性和冗余性，因此有必要对数据进行降维处理，这样既能减少计算量，使数据结构更加清晰，又有利于提高数据分析效率。降低数据维度的办法主要有特征选择和特征抽取，前者是从原始特征子集中进行选择，去除冗余性的特征以及与目标特征不相关的特征[1]；而特征抽取是基于原始特征再创造新特征的方法，也是本文研究重点。线性特征抽取算法主要有主成分分析(PCA)[2]和线性判别分析(LDA)[3]；非线性特征抽取算法主要有局部线性嵌入(LLE)[4]、拉普拉斯特征映射(LE)[5]、等度量映射(Isomap)[6]、多维缩放(MDS)[7]等。

主成分分析是无监督的线性降维算法，其假设数据服从高斯分布，分析时使用的是协方差矩阵，但协方差矩阵只能衡量特征之间的线性关系。因此，针对数据分布特点，研究者提出各种改进措施，如只能处理非高斯数据的独立主成分分析(ICA)[8]、综合算法ICA-PCA[9]、Box-Cox变换[10]、基于支持向量数据描述的ICA-SVDD[11]等；针对数据的非线性关系，研究者提出了基于信息量的PCA[12]、基于最大信息系数和对数变换的PCA[13]、基于核函数的KPCA[14]等改进方法。

Yeo-Johnson变换[15]是一种将非高斯分布数据转化为高斯分布数据的方法，其性能和变换效果比Box-Cox变换更优。而最大信息系数(MIC)[16]是一种衡量属性间相关性的方法，不仅能度量变量间的线性关系，也能度量其非线性关系以及非函数关系。MIC方法具有普适性，即适用于变量间任意形式的函数,同时其还具有公平性[16-17]，即对于不同形式函数存在的相同水平噪声能得到同样的结果。

本文针对PCA中假设数据服从高斯分布且协方差矩阵只能衡量变量之间线性关系的局限，提出一种基于Yeo-Johnson变换和MIC的PCA特征抽取算法。首先利用Yeo-Johnson变换将数据进行转化，使其近似服从高斯分布，满足PCA的假设，再运用MIC将PCA中数据之间存在线性关系的假设推广到非线性关系以及其他关系,最后通过实际数据来分析所提出的改进算法的有效性。

1 主成分分析

主成分分析假设数据服从高斯分布且数据间线性相关，将原始存在相关性的特征重新组合成新的少数几个线性无关的特征，使得投影后的特征子空间在每个维度上的数据方差达到最大，新形成的子空间特征即为主成分，各个主成分互不相关，且数量比原始特征少，按照所在方向的方差贡献率降序排列。主成分包含了原始变量的大多数信息，所包含的信息更凝聚。

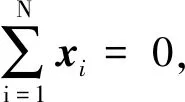
(1)

使得基于投影重构的样本点x(i)′和原样本点x(i)之间的距离即整体误差达到最小。进一步化简后，优化目标为：

(2)

经过求解，最终转化为求XXT的特征值问题。对矩阵XXT进行特征值分解得到特征值(λ1,λ2,…,λp)，以及对应的特征向量(u1i,u2i,…,upi),i=1,2,…,p。设X=(X1,X2,…,Xp)T，则主成分为Zi=u1iX1+u2iX2+…+upiXp，i=1,2,…,p。再选取特定个数的主成分，组成新的样本数据，一般选择出的k个主成分对应特征值之和占总体特征值之和的85%以上即可。为了不损失过多信息，本文取主成分阈值为95%。

2 改进的主成分分析算法：YJ-MICPCA

2.1 Yeo-Johnson变换

Yeo-Johnson变换的公式如下[15]：

(3)

式中：y为需要变换的数据；λ为需要估计的未知参数，可利用极大似然法进行参数估计。Yeo-Johnson变换能改善数据的正态性和对称性。

2.2 最大信息系数

MIC方法的基本原理是：将两个变量构成的集合记为数据集D(x,y)，把坐标平面划分成x列y行的网格，网格上的每个小单元G的概率为G中的点数除以网格上的总点数，这样得到二元数据集在网格上的概率分布D|G。数据集可以有很多划分方法，对于每种划分方式计算互信息I(D|G)，取所有划分方式中的最大值，有I*(D,x,y)=maxI(D|G)，所以最大信息系数计算公式为：

(4)

式中：N为样本数；B(N)为样本的函数，所划分网格的小单元总数要小于B(N)，根据文献[16]，取B=N0.6。本文利用MIC改进PCA只能处理线性关系的不足。

2.3 YJ-MICPCA算法

PCA算法中要求数据服从高斯分布。二维高斯分布中独立和不相关是等价的，当数据服从高斯分布时，得到的主成分之间协方差cov(Fi,Fj)=0(i≠j)，即主成分不相关，等价于独立，进而保证了主成分之间无信息重叠，同时高斯分布下数据的主要信息会得到较好的保留。当数据服从非高斯分布时，会发生尺度缩放与旋转，并且主成分之间不一定独立，最后结果会产生偏差。因此，本文首先运用Yeo-Johnson变换将非高斯分布数据进行转化，使其近似服从高斯分布，满足PCA算法的前提假设。

PCA中运算使用的是协方差矩阵，但协方差矩阵只能衡量特征之间的线性关系，现实问题中数据间可能存在非线性以及非函数等较复杂的关系，因此本文运用MIC改进PCA。同时，PCA运算中协方差矩阵是非负定的，在进行特征值分解时，得到的特征值恒大于0。将协方差矩阵换成最大信息矩阵后，不一定满足这一条件，因此，改进算法采用最大信息系数矩阵的平方，记为M，这样就能保证矩阵M是非负定的。下面对此进行证明。

要证明矩阵M是非负定的，只需证明：对任意向量y，有yTMy≥0。设随机向量X=(X1,X2,…,Xp)，任意两个变量之间的最大信息系数mic(Xi,Xj)利用式(4)计算，得到最大信息系数矩阵

Q=

则M=Q2。

因为Q为实对称矩阵，故Q=QT，所以对于任意向量y，有yTMy=yTQQTy=‖yTQ‖2≥0，即矩阵M非负定，从而保证在特征值分解时，得到的特征值均为非负。

综上，改进算法YJ-MICPCA如下：

输入数据集D={x1,x2,…,xN}，每个样本的p个特征F={F1,F2,…,Fp}，类别Y; 主成分阈值t=95%。

输出特征投影后的新数据集DD={z1,z2,…,zN}。

步骤2根据式(4)，计算Yeo-Johnson变换后数据的MIC矩阵Q，进而得到MIC平方矩阵M。

步骤3对矩阵M进行特征值分解，得到特征值(λ1,λ2,…,λp)以及对应的特征向量。

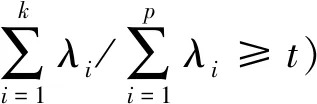
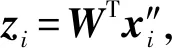
3 实验及结果分析

3.1 数据集

实验所用的11个数据集均来自UCI机器学习数据库，如表1所示。实验基于Python和R语言编程，系统运行环境为：Intel(R) Core(TM)i5-3337U 处理器，1.8 GHz CPU,4 GB RAM，Win 8操作系统。

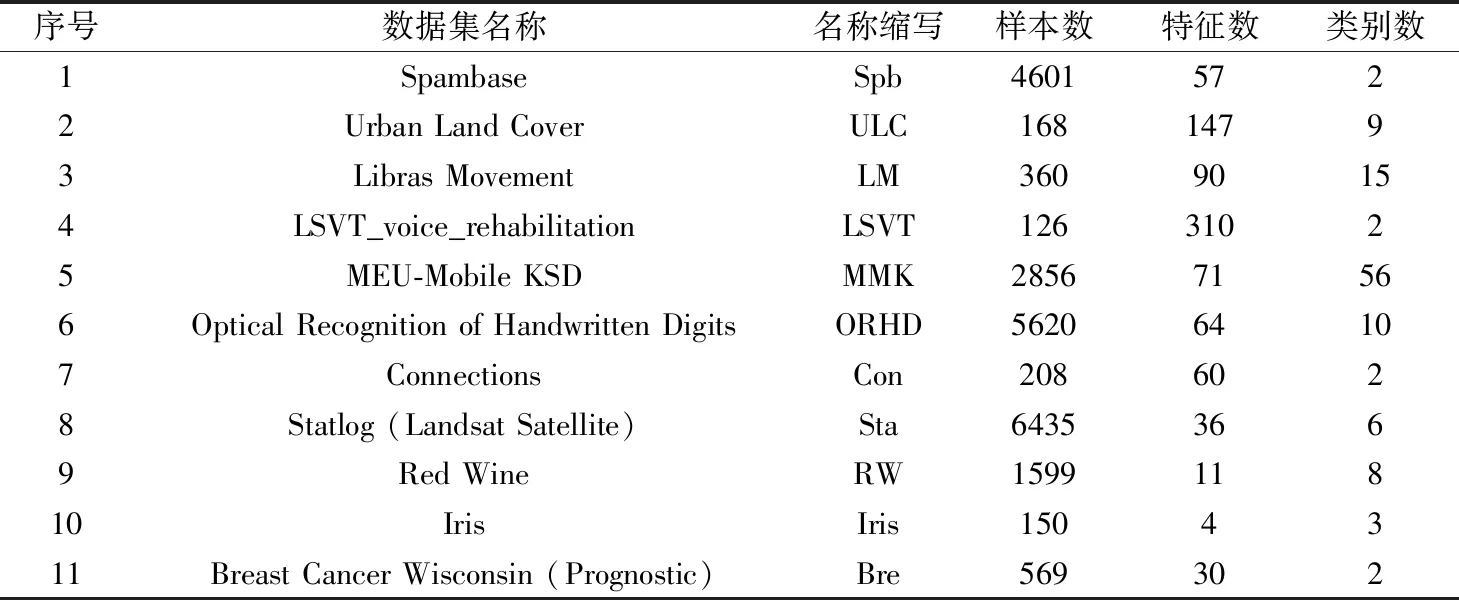
表1 实验数据集描述

为了对比分析，除了采用本文提出的改进算法之外，还采用PCA[2]、KPCA[14]、LLE[4]、Isomap[6]、MSD[7]这5种算法对数据进行降维处理，并利用非线性支持向量机(SVM)[18]、朴素贝叶斯模型(NB)[19]和k近邻算法(k-NN)[20]这3种应用较为广泛的分类器对降维后的数据进行分类，然后进行结果分析，以最终分类精度为基准，所有数据采用50次5折交叉验证。

3.2 分类器参数设置

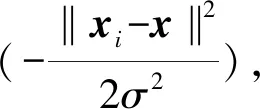
采用k-NN分类器计算距离时，为了消除数据尺度不同对结果的影响，计算前需要对数据进行标准化处理。本文中k分别取1,2,…,10这几个值，在原数据集上进行实验，通过50次5折交叉验证选择平均分类准率最高时的k值作为其最终取值。

3.3 结果分析

首先，比较YJ-MICPCA和PCA两种算法在主成分阈值t=95%(即信息损失为5%)时的分类准确率和数据维度，分别见表2和表3，表2中还列出了未降维的原始数据集的分类准确率。

从表2可以看到(表中粗体部分显示YJ-MICPCA比PCA分类精度高)：对于数据集MMK和ORHD，采用3种分类器，YJ-MICPCA均比PCA方法获得较高的分类精度，最大差距为17.18个百分点；采用SVM分类器时，对于数据集RW和Iris，YJ-MICPCA比PCA的处理效果更优；采用NB分类器时，在数据集Con、RW和Bre上，YJ-MICPCA比PCA效果更优；采用k-NN分类器时，在数据集Spb和Con上，YJ-MICPCA比PCA效果更优；而对于其余数据集，PCA比YJ-MICPCA的分类精度略高，最大差距为13.51个百分点。总体来看，当t=95%时，PCA在大多数数据集上的分类精度略优于YJ-MICPCA。

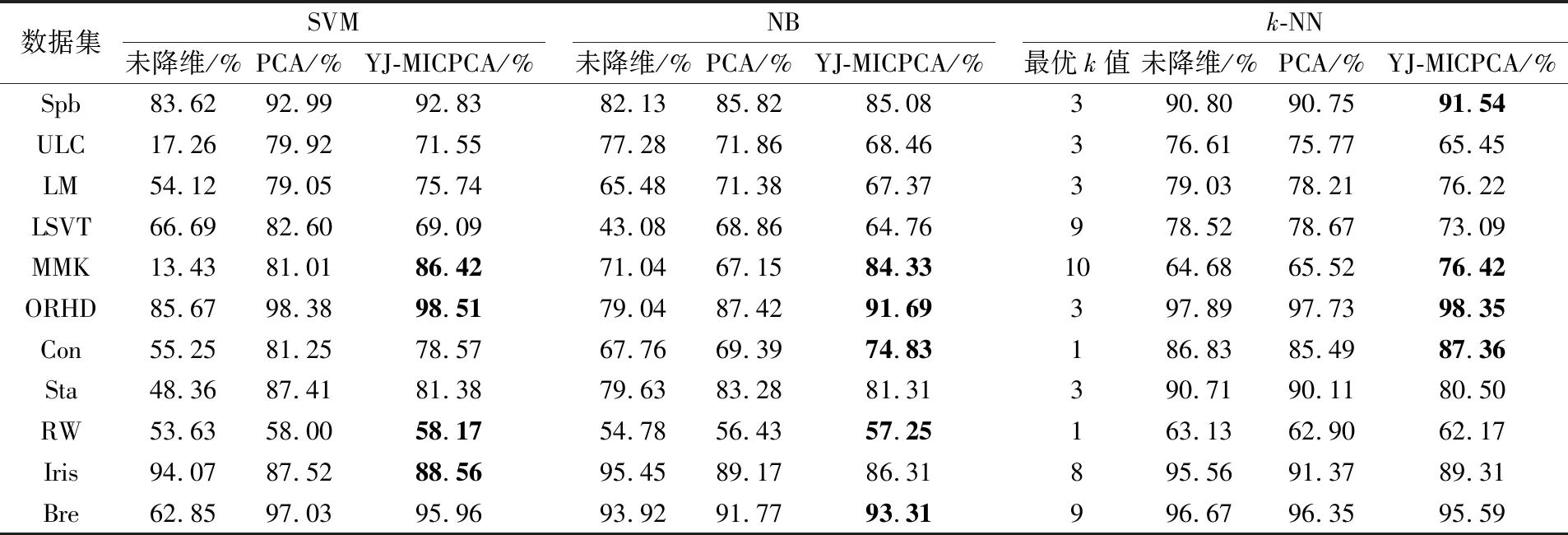
表2 YJ-MICPCA和PCA算法取t=95%时的分类准确率

表3 采用YJ-MICPCA和PCA算法得到的数据维度(t=95%)

Table 3 Dataset dimensionalities reduced by YJ-MICPCA and PCA algorithms(t=95%)

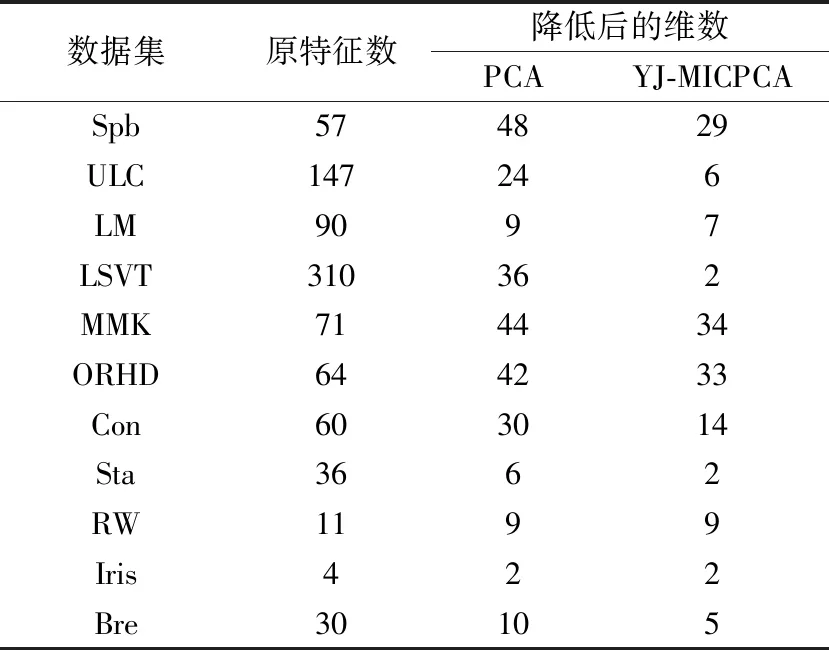
数据集原特征数降低后的维数PCAYJ-MICPCASpb574829ULC147246LM9097LSVT310362MMK714434ORHD644233Con603014Sta3662RW1199Iris422Bre30105

从表3可以看到，当t=95%时，与原始特征数量相比，PCA和YJ-MICPCA两种算法均达到了降维效果，但是YJ-MICPCA的降维程度要优于PCA。YJ-MICPCA对LSVT数据集的降维程度高达99.355%，而PCA的最大降维程度为90%(LM数据集)。根据这两种算法的不同之处可知，YJ-MICPCA算法更能检测到数据之间的关系，在相同维度下，其信息保留能力更强，所包含的信息更凝聚。

然后，比较相同维度下PCA和YJ-MICPCA算法的分类准确率。以PCA算法在t=95%时得到的数据维度为基准，两种算法在该维度下的分类准确率见表4。从表4可以看到，针对不同分类器和绝大部分数据集，YJ-MICPCA均比PCA的分类精度高，最大相差18.28个百分点(MMK数据集，NB分类器)，而对于少数几个数据集，PCA的分类精度较高，最大差距为12.69个百分点(Spb数据集，NB分类器)。总体来说，相同维度下采用不同分类器时，YJ-MICPCA比PCA得到的分类精度更优。

表4 YJ-MICPCA和PCA算法取相同维度时的分类准确率(单位：%)

下面比较不同维度(即主成分个数)变化时，PCA和YJ-MICPCA这两种特征抽取算法的最高分类精度及分类精度随维度的变化情况。降维后的数据服从高斯分布，并且特征之间不相关，正好满足高斯朴素贝叶斯分类器的条件，同时，考虑到参数调节、运算复杂度和文章篇幅等问题，以下仅列出采用高斯朴素贝叶斯分类器时各数据集的分类准确率最大值(如表5所示)，以及LSVT数据集的分类准确率随维度变化情况(如图1所示)。

表5 采用NB分类器时YJ-MICPCA和PCA算法的分类准确率最大值(单位：%)

Table 5 Maximal classification accuracies of YJ-MICPCA and PCA algorithms using NB classifier

数据集PCAYJ-MICPCASpb86.7288.75ULC76.7380.34LM82.1483.57LSVT69.2077.51MMK67.8586.58ORHD88.4391.97Con76.4179.26Sta83.8684.36RW56.5858.68Iris92.4689.26Bre92.8595.32

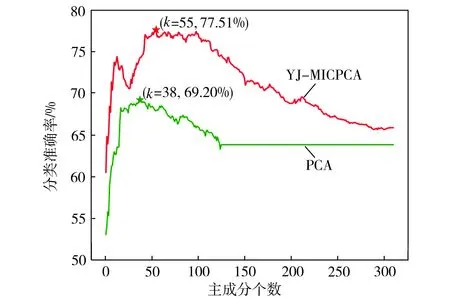
图1 LSVT数据集的分类准确率随维度的变化

Fig.1 Variation of classification accuracy of dataset LSVT with dimensionality

从表5可以看到，在11个数据集中，有10个数据集采用YJ-MICPCA算法的分类精度高于PCA算法，二者最大差距为18.73个百分点(MMK数据集)；只在Iris数据集上PCA算法较优，二者仅相差3.2个百分点。从图1可以看到，不同维度下，PCA和YJ-MICPCA两种算法的分类精度变化趋势基本相同，即随着维度的增加，分类准确率先上升达到最高点，然后又逐渐降低，并且在同一维度值时，YJ-MICPCA所获得的分类精度均高于PCA。结合其他数据集的实验结果，可以得出YJ-MICPCA算法较PCA算法的特征抽取效果更好的结论。

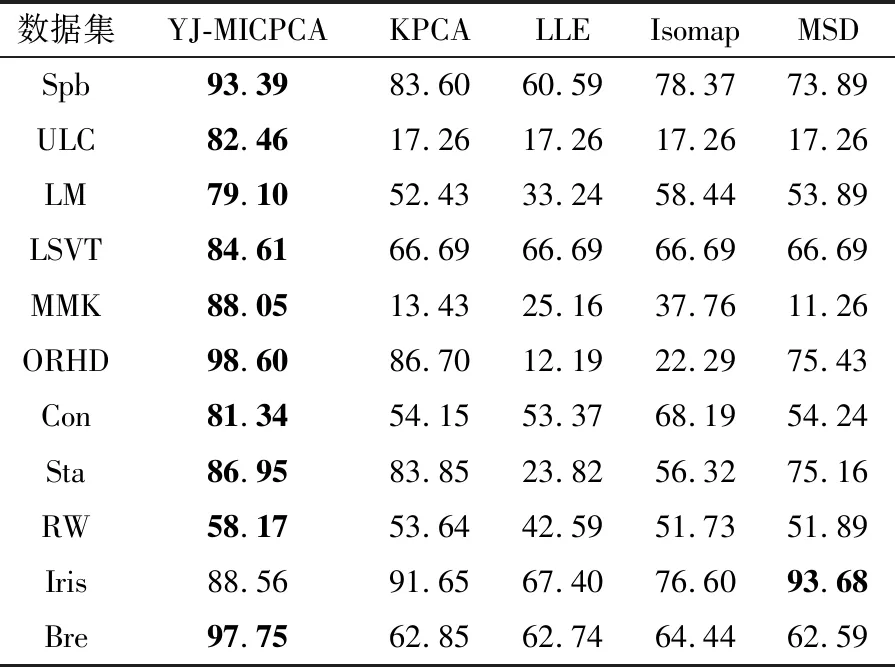
最后，在相同维度下比较YJ-MICPCA与其他非线性降维方法(LLE、Isomap、MSD、KPCA)的总体分类精度，以PCA在t=95%时的维度为基准，得到结果如表6～表8所示(表中粗体部分显示各数据集的分类准确率最大值)。从表中可以看出，采用不同分类器时，在大多数数据集上YJ-MICPCA算法较其他方法均占有优势，分类精度更高。

表6 采用SVM分类器时5种算法的分类准确率(单位：%)

Table 6 Classification accuracies of five algorithms using SVM classifier

数据集YJ-MICPCAKPCALLEIsomapMSDSpb93.3983.6060.5978.3773.89ULC82.4617.2617.2617.2617.26LM79.1052.4333.2458.4453.89LSVT84.6166.6966.6966.6966.69MMK88.0513.4325.1637.7611.26ORHD98.6086.7012.1922.2975.43Con81.3454.1553.3768.1954.24Sta86.9583.8523.8256.3275.16RW58.1753.6442.5951.7351.89Iris88.5691.6567.4076.6093.68Bre97.7562.8562.7464.4462.59

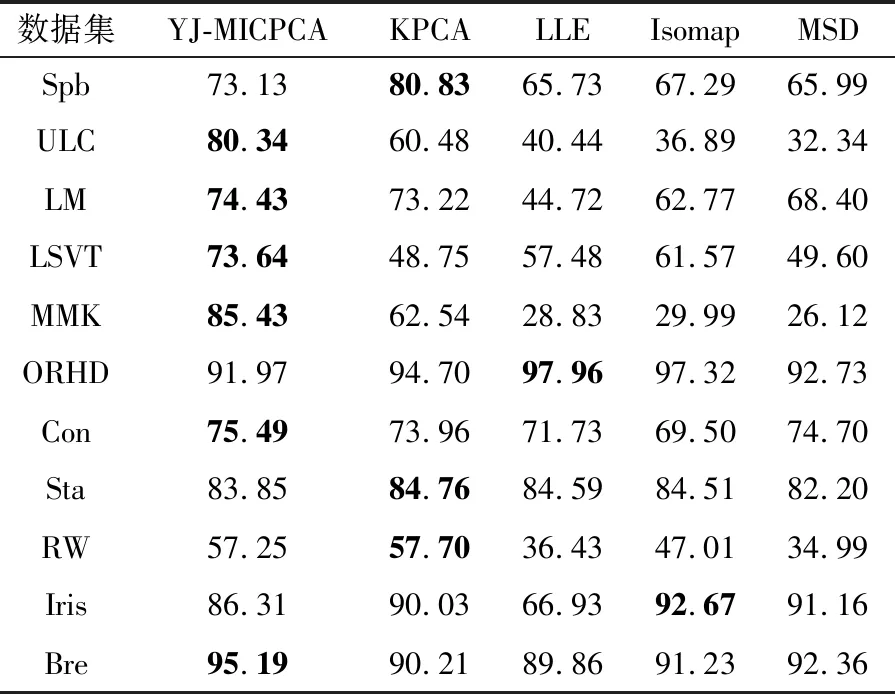
表7 采用NB分类器时5种算法的分类准确率(单位：%)

Table 7 Classification accuracies of five algorithms using NB classifier

数据集YJ-MICPCAKPCALLEIsomapMSDSpb73.1380.8365.7367.2965.99ULC80.3460.4840.4436.8932.34LM74.4373.2244.7262.7768.40LSVT73.6448.7557.4861.5749.60MMK85.4362.5428.8329.9926.12ORHD91.9794.7097.9697.3292.73Con75.4973.9671.7369.5074.70Sta83.8584.7684.5984.5182.20RW57.2557.7036.4347.0134.99Iris86.3190.0366.9392.6791.16Bre95.1990.2189.8691.2392.36

表8 采用k-NN分类器时5种算法的分类准确率(单位：%)

Table 8 Classification accuracies of five algorithms usingk-NN classifier

数据集YJ-MICPCAKPCALLEIsomapMSDSpb91.2480.7376.3377.9375.31ULC78.9843.7042.9041.4043.19LM78.0677.0267.5872.2477.98LSVT78.8762.8657.4062.7562.82MMK76.5943.3434.5838.7740.75ORHD98.4498.7498.8298.5897.60Con87.2482.5479.0979.2180.79Sta89.5590.2186.6888.7289.88RW62.1758.3757.9156.5355.61Iris89.3195.8969.0196.3295.88Bre96.2593.1292.4893.0592.98

4 结语

本文提出了一种改进的PCA特征抽取算法YJ-MICPCA，它能处理数据特征间存在的线性、非线性以及非函数关系。该算法先改善数据分布，使其近似满足PCA要求的高斯分布假设，并将PCA中计算协方差矩阵转化为计算最大信息系数矩阵的平方，从而将PCA算法推广为非线性特征抽取算法。在主成分阈值为95%的条件下，采用11个数据集、3种分类器来对比分析PCA和YJ-MICPCA的数据降维效果，比较了50次5折交叉验证下的平均分类精度和维度、相同维度下的平均分类精度以及不同维度下的分类准确率最大值,同时还比较了YJ-MICPCA和其他4种非线性降维算法的性能。实验结果证明了YJ-MICPCA算法识别数据中复杂关系的能力比PCA强，特征抽取效果更优，并且YJ-MICPCA与其他非线性降维算法相比也具有优势。