原子无序对half-Heusler合金CoCrAl电子结构及Seebeck系数的影响
2019-05-18李春蓉卢志红王文静
李春蓉,卢志红,王文静,尹 航
(武汉科技大学省部共建耐火材料与冶金国家重点实验室,湖北 武汉,430081)
热电材料基于热电效应能实现热与电的相互转换,可用于温差发电或固态制冷领域,由该类材料制作的元器件具有无噪音、低污染、寿命长以及易于维护等一系列优点[1-2]。热电材料的能量转换效率可用无量纲参数热电优值ZT来衡量,表达式为ZT=σS2T/κ,式中σ、S、T和κ分别表示材料的电导率、Seebeck系数、绝对温度和热导率,其中σS2被称为功率因子[3]。可见,为了获得较高的ZT值,可通过提高材料功率因子或降低其热导率来实现。根据理论计算分析,当热电材料的ZT值为3时,其能量转换效率可与传统热机(转换效率为30%~40%)相媲美[4],目前Zhao等[5]制备的SnSe单晶热电材料ZT值已达到2.6。而half-Heusler合金因其较大的Seebeck系数、良好的电导率、高熔点和高温稳定性,被认为是具有研发潜力的理想热电材料之一,特别是其中物理学原胞价电子数总和为18的一些化合物体系,如ZrNiSn、HfNiSn、TiCoSb和FeNbSb等具有较窄的禁带宽度、较大的载流子有效质量及Seebeck系数,因此热电性能更佳。Fu等[6]报道了p型FeNbSb合金在1200 K高温条件下的ZT值高达1.5。Shutoh等[7]的研究表明,室温下ZrNiPb的Seebeck系数为-153.9 μV/K,其功率因子高于Zr0.5Hf0.5NiSn在700 K时的相应值。Hermet等[8]利用第一性原理计算了NiTiSn的晶格热导率,计算结果同该材料在700 K时的实验值一致,并且证实了材料晶格热导率深受其晶粒大小影响。Xue等[9]计算得出LaPtSb化合物的室温晶格热导率为1.72 W/(m·K),是目前已报道的half-Heusler化合物晶格热导率最低值,其ZT值最高可达2.2。当前该类热电材料研究主要集中在ZrNiSn基和FeNbSb基化合物,而价电子数同为18的half-Heusler合金CoCrAl的热电性能却鲜有报道,有鉴于此,本文结合理论分析与实验测试,探讨了CoCrAl合金中原子占位对其电子结构、磁性和Seebeck系数的影响,以期为该材料在热电领域的研究与应用提供参考。
1 理论计算与实验方法
1.1 模拟与计算方法
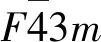
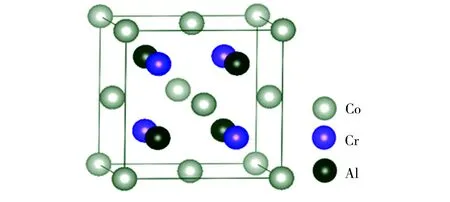
图1 CoCrAl合金的C1b型晶体结构
本文针对CoCrAl合金晶体结构及电子特性的理论研究主要基于密度泛函(DFT)理论的第一性原理,采用VASP软件包进行模拟计算。借助全势线性缀加平面波(FP-LAPW)方法生成的广义梯度近似(GGA)方法处理电子之间的交换关联能。通过收敛性测试后,平面波截断能设为550 eV,弛豫和静态计算均采用Monkhorst-Pack方法产生的15×15×15点网格精度进行布里渊区能量积分。在结构弛豫过程中,能量收敛标准为10-6eV,力收敛标准为0.1 eV/nm。此外,在进行CoCrAl合金电子结构的自洽计算时,采用31×31×31点网格精度进行布里渊区积分以获得电子群速度和较高的能量本征值。结合电子的玻尔兹曼输运理论计算CoCrAl材料在不同温度下的Seebeck系数,计算温度区间设置为300~800 K,温度梯度为50 K。
1.2 实验方法
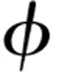
2 结果与讨论
2.1 模拟计算结果与讨论
计算得到C1b、XY及YZ结构CoCrAl合金的总态密度图如图2所示,相应的晶格常数、磁矩以及能量模拟计算结果列于表1。从图2中可以看出,具有C1b有序结构的CoCrAl合金自旋向上和自旋向下的态密度完全对称,此外,在其费米能级附近存在一个较窄的赝能隙,使得该合金表现出典型非磁性金属特性;具有XY无序结构的CoCrAl合金自旋向上和自旋向下的态密度也完全对称且显示出非磁性金属特性;具有YZ无序结构的CoCrAl合金自旋向上和自旋向下的态密度对称性遭到破坏且相应费米能级均有电子态分布,显示出磁性金属特性。基于Galanakis等[11]建立的轨道杂化模型,带隙两侧的宽度应取决于Co原子间的相互作用,在具有有序结构的CoCrAl合金中,Co原子首先与近邻不同占位的Co原子发生3d轨道杂化,然后这些杂化轨道继续与Cr原子3d轨道杂化,最终分别在低于和高于费米面处形成成键态和反键态,Co—Co杂化后形成的反键态因与Cr原子的3d轨道不在同一表象而得以保留,带隙大小即为反键态之间的能量差。
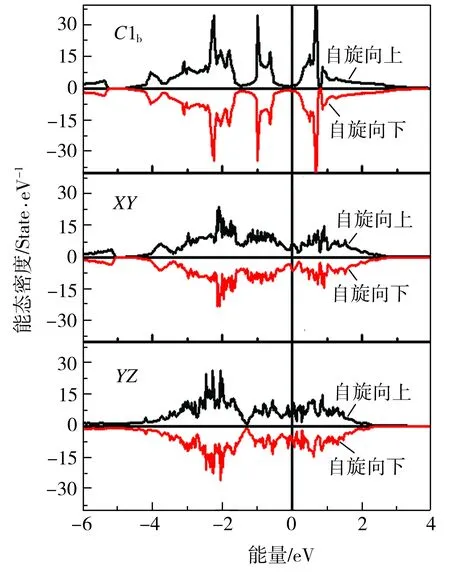
图2 CoCrAl合金的总态密度图
当合金中原子发生无序占位时,轨道杂化情况非常复杂,各原子间相互作用机理尚未厘清,仍需深入开展研究。由表1可见,CoCrAl合金为C1b有序结构时的晶格常数为0.5460 nm,而其为XY或YZ无序结构时的相应值均明显增大,表明样品晶格常数的变化同其结构无序化所导致的晶格畸变有关。三种结构类型中只有YZ无序结构所对应的合金晶胞磁矩不为0,这表明该结构对合金磁性影响较大。在平衡状态下,三种结构类型的CoCrAl合金单胞总能均为负值,且合金为无序结构时的能量值明显高于其为有序结构时的相应值,这表明该合金可以通过实验合成且其在平衡态时发生无序转变的难度较大。此外XY和YZ无序结构合金之间单胞能量差值较小,表明在平衡状态下,这两种无序转变在合金中发生的几率几乎相等。
表1 CoCrAl合金的晶格常数、磁矩及能量
Table 1 Lattice constants, magnetic moments and energy of CoCrAl alloy

结构类型晶格常数/nm磁矩/μB·(f.u.)-1能量/eVC1b0.54600-80.71XY0.54930-79.04YZ0.54800.2-79.09
图3为理论计算所得C1b、XY及YZ结构CoCrAl合金的Seebeck系数随温度的变化曲线。由图3可见,在计算采用的温度区间内,三种结构类型的CoCrAl合金Seebeck系数皆为负值,表明该合金以电子作为传导载流子;在同一温度下,CoCrAl合金为C1b结构时的Seebeck系数(绝对值)最大而为XY结构时的相应值最小,这表明结构有序性对合金Seebeck系数影响较大。当原子排列无序时,晶格缺陷增多从而导致原子散射增强,而原子散射增强将会造成Seebeck系数(绝对值)下降[12]。在相同衍射角度下,Co、Cr、Al原子的散射因子依次降低,所以XY型(Co、Cr原子无序)结构的原子散射强于YZ型(Cr、Al原子无序)结构,故前者Seebeck系数(绝对值)最小。此外,三种合金的Seebeck系数(绝对值)均随温度的升高而先增后减,并且都在400 K左右达到最大值。这是因为当温度低于400 K时,升高温度可激发声子的散射,导致载流子浓度不断增加且此时电子传导占优势,故而材料Seebeck系数(绝对值)不断增高;当温度继续升高超过400 K以后,载流子在温度较高的情况下发生了本征激发,声子间的相互作用变强,此时,材料Seebeck系数(绝对值)因晶格振动的不断加剧而表现出下降的趋势[13]。
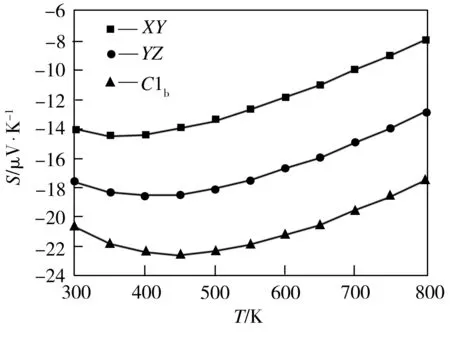
图3 计算所得CoCrAl合金Seebeck系数随温度的变化
Fig.3 Variation of calculated Seebeck coefficients of CoCrAl alloy with temperature
2.2 实验结果与讨论
实验测得CoCrAl合金的XRD谱图如图4所示。由图4可见,实测样品XRD谱图中除了对应其晶粒优势生长取向(220)晶面的特征峰外,还存在较弱的(200)及(111)晶面衍射峰,并且(111)面衍射峰相比(200)面更弱。而理论上根据结构因子关系式及消光条件可知,C1b有序、XY或YZ无序结构的CoCrAl合金XRD图中均将出现明显的(111)和( 200 )晶面衍射峰,且合金结构为C1b有序时其(111)面衍射峰相比(200)面应更强。实测结果与理论分析之间的差异应归因于实验制备样品中存在无序结构。此外,根据XRD测试结果可求得CoCrAl合金晶格常数为0.5730 nm,明显高于其为C1b有序结构时相应的理论计算值,这再次表明该合金晶体结构并非完全有序,其中应存在XY或YZ等无序结构。

图4 CoCrAl合金的XRD图谱
实验测得CoCrAl合金样品在10 K下的磁化曲线如图5所示。由图5可见,该合金样品的磁滞回线较窄,其饱和磁矩约为0.75 emu/g,即0.074 μB/f.u.。而Slater-Pauling(S-P)规则指出,half-Heusler合金的单胞总磁矩Mt是原胞中价电子总数Zt的函数,数学表达式为Mt=Zt-18[14],故可以计算出原胞价电子总数为18的CoCrAl合金的饱和磁矩为0;结合图2所示的总态密度图可知,CoCrAl合金为C1b和XY结构时表现出非磁性而为YZ结构时表现出磁性,故推测实验测得合金的磁性来自于实际样品中的YZ结构。图6为实验测得CoCrAl合金的Seebeck系数随温度的变化曲线。由图6可以看出,实测CoCrAl合金的Seebeck系数随温度变化的规律同其理论计算结果(见图3)一致,且数值与其中XY结构的CoCrAl合金相应值最为接近,表明实际样品中存在XY无序结构。根据表1理论计算结果分析可知,平衡态下XY与YZ无序结构所对应的合金单胞能量十分接近,二者发生的概率几乎相等,结合CoCrAl合金磁化曲线及Seebeck系数实测结果表明,CoCrAl合金样品中应同时存在XY与YZ无序结构。
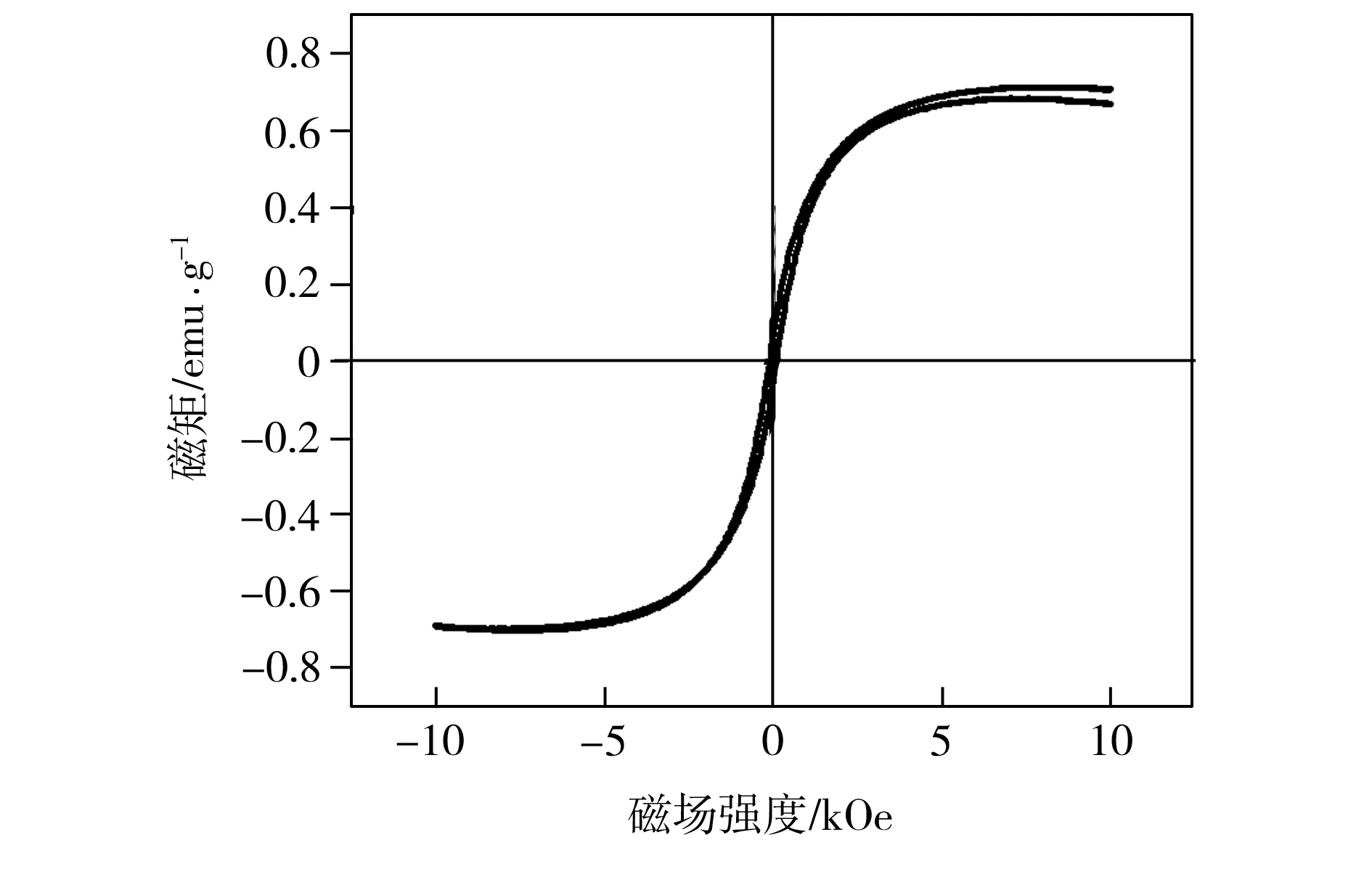
图5 CoCrAl合金在10 K下测得的磁化曲线
Fig.5 Magnetization curve of CoCrAl alloy measured at 10 K

图6 CoCrAl合金的Seebeck系数随温度的变化情况
Fig.6 Variation of Seebeck coefficients of CoCrAl alloy with temperature
3 结语
基于密度泛函理论的第一性原理计算可知,具有C1b有序结构的half-Heusler合金CoCrAl在费米能级处有较窄的赝能隙,是潜在的热电材料。本研究采用真空电弧熔炼及放电等离子烧结技术制备了CoCrAl合金,根据该合金XRD衍射谱、饱和磁矩及Seebeck系数实测结果与利用VASP和BoltzTraP软件包对其理论模拟计算所得数值对比分析可知,CoCrAl合金为C1b有序或XY无序结构时表现出非磁性而为YZ无序结构时则显示出磁性特性,合金样品饱和磁矩实测值不为0应归因于其中存在YZ无序结构,其Seebeck系数实测值与其结构为XY无序时的理论计算值较吻合,表明实际样品中同时存在XY无序结构,样品实际晶格常数高于理论值应为两种无序结构共同影响的结果。
