平面膜结构预张力和变形的蠕变效应分析

李延民，秦书祺，张建立

(郑州大学机械工程学院，河南 郑州，450001)

膜材作为常用的建筑材料，需具备良好的物理及力学性能，而膜结构的预张力是保证其造型和功能的关键所在，预张力的大小决定了膜结构的外观状况和承载能力。普通膜材是由织物基材和聚合物涂层构成的复合材料，具有与聚合物相似的黏弹性特征，随着时间的推移将会发生蠕变。蠕变是指固体材料在保持应力不变的条件下，应变随时间延长而增加的现象。蠕变不仅会导致膜材变形量加大，产生形态变化，甚至还有可能使膜材丧失结构功能[1]。因此，在膜结构的设计过程中，要充分考虑蠕变对其预张力和形变的影响。

目前，已有众多学者针对膜结构的蠕变性能展开研究。于波等[2]基于索膜结构蠕变性能，提出了适合该类膜结构的本构模型、测试方案以及对其进行有限元分析的方法；许珊珊等[3]对PTFE膜材进行了5种温度条件下的单轴应力松弛试验，发现大部分黏弹性本构关系模型都能对PTFE膜材的应力松弛行为做出较好的预测；刘海卿等[4]利用黏弹性力学的Burgers四元件模型推导出蠕变对索膜结构影响的有限元方程，然后借助ANSYS软件对该蠕变过程进行模拟验证，分析结果与所推导理论方程相符合。但当前相关研究多针对索膜结构而对平面膜结构蠕变效应的报道较少，为防止平面膜结构因蠕变造成预张力不足或发生破坏，本文从膜结构预张力和膜面变形两方面入手，以工程实例为基础，对平面膜材蠕变性能展开研究，提出合适的蠕变本构模型并推导出相关计算方程，结合理论、仿真分析及试验验证等手段，探讨了膜结构预张力和膜面变形在材料蠕变过程中的变化规律，以期为平面膜结构在实际中的设计安装提供参考。

1 材料的蠕变特性

材料的蠕变过程可分为暂态、稳态和破坏三个阶段[5]，在恒定应力下，材料的蠕变过程如图1所示。从图1中可以看出，在加载瞬间，材料首先出现一个瞬时应变ε0，蠕变第一阶段随后立即开始，在此期间，材料的应变量增长较快，应变速率随时间的延长而不断减小并逐渐趋于稳定，此阶段历时较短，故被称作暂态阶段；在蠕变第二阶段中，材料应变量随时间延长而继续增加，应变速率为稳定值，此阶段材料的应变量增长较为缓慢，持续时间的长短主要取决于应力水平，故被称为稳态阶段；在蠕变过程第三阶段，材料应变和应变速率均迅速增加并引起其内部结构破坏，膜材丧失结构功能，故此阶段又被称为破坏阶段，该阶段分析意义不大，在实际工程中需重点关注的是材料蠕变过程的第一和第二阶段。

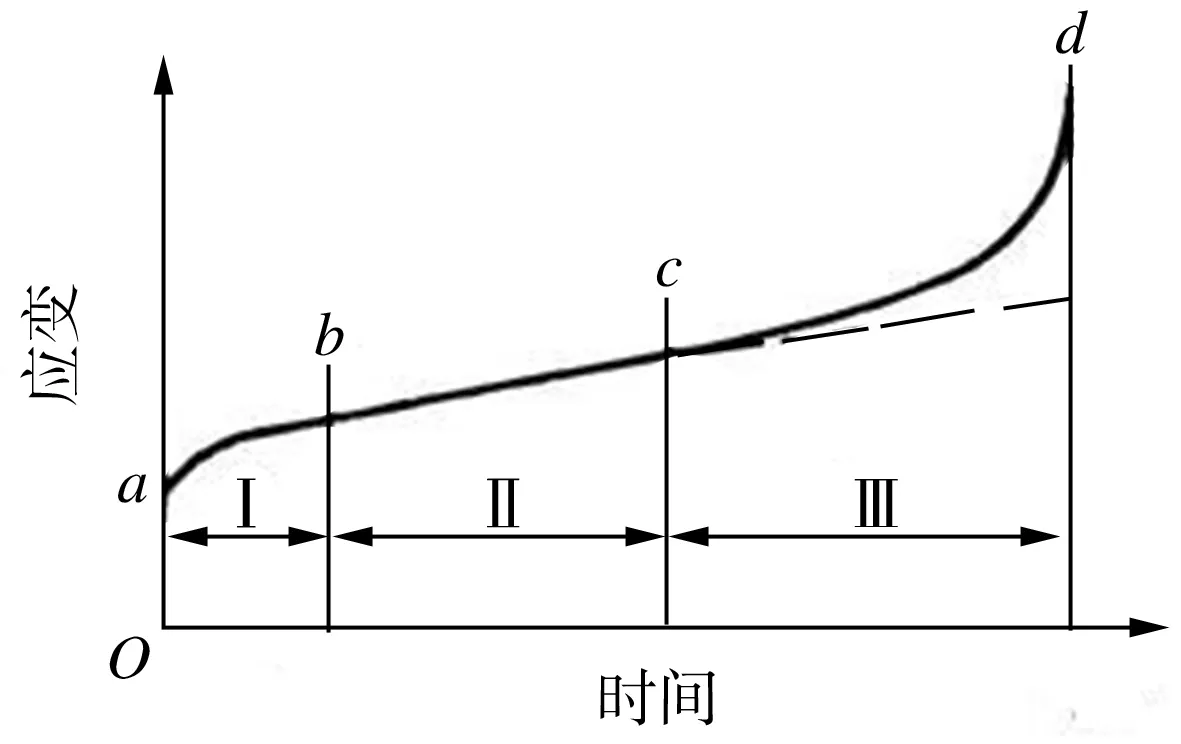
图1 蠕变曲线

2 蠕变本构模型

蠕变的本构模型可采用黏弹性力学或者基于蠕变力学的蠕变模型。常用的黏弹性力学模型有Kelvin 模型、Maxwell模型、Burgers模型、广义线性黏弹性模型及标准线性固体模型，基于蠕变力学的蠕变模型有应变硬化理论模型、时间硬化理论模型、塑性滞后理论模型及恒速蠕变理论模型等，其中改进的时间硬化模型(MTHM)[6]最为实用，其数学表达式为全量形式，蠕变过程由应变、应力和时间来确定，经试验获得的原始数据，不需要进行过多预处理就可直接用于该模型，故本文ANSYS仿真分析及理论计算公式推导均以此模型为基础，模型数学表达式为

(1)

式中：εc为蠕变应变；σ为对膜材施加的应力，MPa；t为膜材蠕变持续时间，h；T为膜材蠕变时的温度，K；C1、C2、C3、C4为与材料相关的常数，由 PTFE 膜材的蠕变试验确定。

3 工程实例及分析

3.1 工程实例

某建筑中屋顶部位需要安装平面骨架膜结构，骨架结构由多个相同的矩形框架拼接而成，每个框架都连接着膜材，则整体膜结构的蠕变效应与单个框架上膜材的蠕变效应相同，故仅需以单个框架膜结构为研究对象。框架尺寸为3.15 m×2.5 m，几何模型如图2所示。膜材选用PTFE涂层材料，其厚度为0.63 mm，初始预张力为18 MPa。

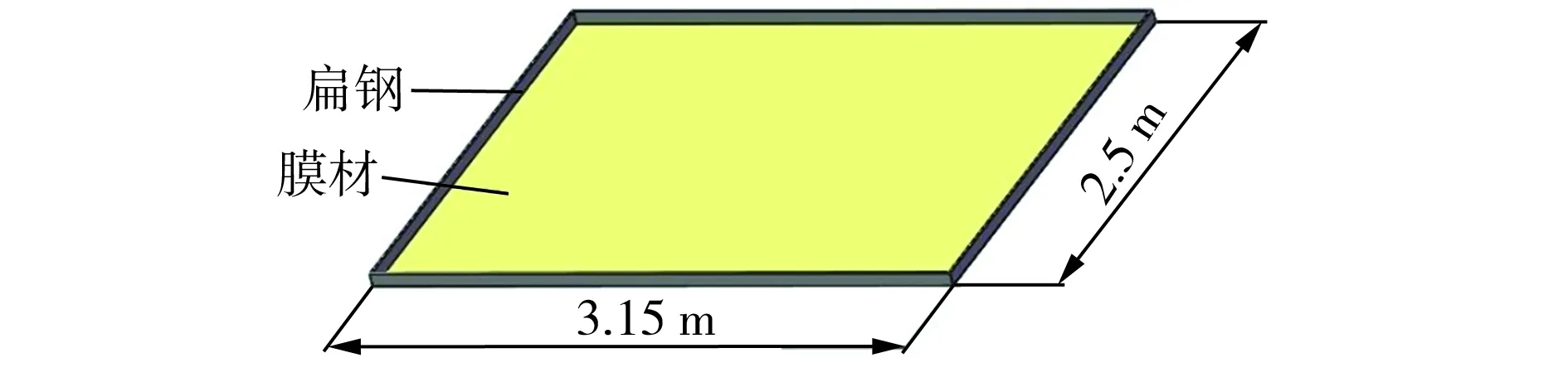
图2 简化的膜结构模型

3.2 ANSYS仿真分析

3.2.1 膜结构预张力与蠕变的关系

工程实例中膜结构预张力与蠕变的关系借助ANSYS中的Static Structural模块进行概念建模。首先将膜结构四周框架设定为固定约束，根据文献[7]，在常温下，PTFE模材经向的弹性模量比其纬向相应值高7.2%，因此将膜材按各向同性膜处理也不会影响其蠕变时的变化趋势。设置膜材弹性模量为1.82 GPa，泊松比为0.3，蠕变参数C1、C2、C3、C4的值分别设定为0.00484、0.35564、-0.898 44、0。通过APDL指令设置单元类型为SHELL181，初始预张力为18 MPa并设置两个载荷步，第一步不考虑蠕变，用时1 s，在此期间预张力保持不变；第二步考虑蠕变，用时105s，将此阶段等分为100个子步，由此得到膜结构预张力与时间的关系如图3所示。从图3中可以看出，在蠕变影响下膜结构预张力呈整体下降的趋势，尤其在第一个子步中膜结构预张力下降最快，之后随着时间的延长其下降速度逐渐变慢并趋近稳定，符合材料蠕变的第一和第二阶段特征。提取不同时间段的蠕变数据进行对比表明，在1～1000、1001～2000、2001～3000 s时间段内膜结构预张力分别下降了6.53×105、8.2×104、5×104Pa，下降速度很快并且各时间段内降幅差别明显。而在9.9×104～1×105s区间内膜结构预张力仅下降了1000 Pa，降幅较小。整体来看，在105s测试时间内，膜结构预张力总计下降了1.27 MPa，降幅约7%，尚在实际工程中可接受的范围内。

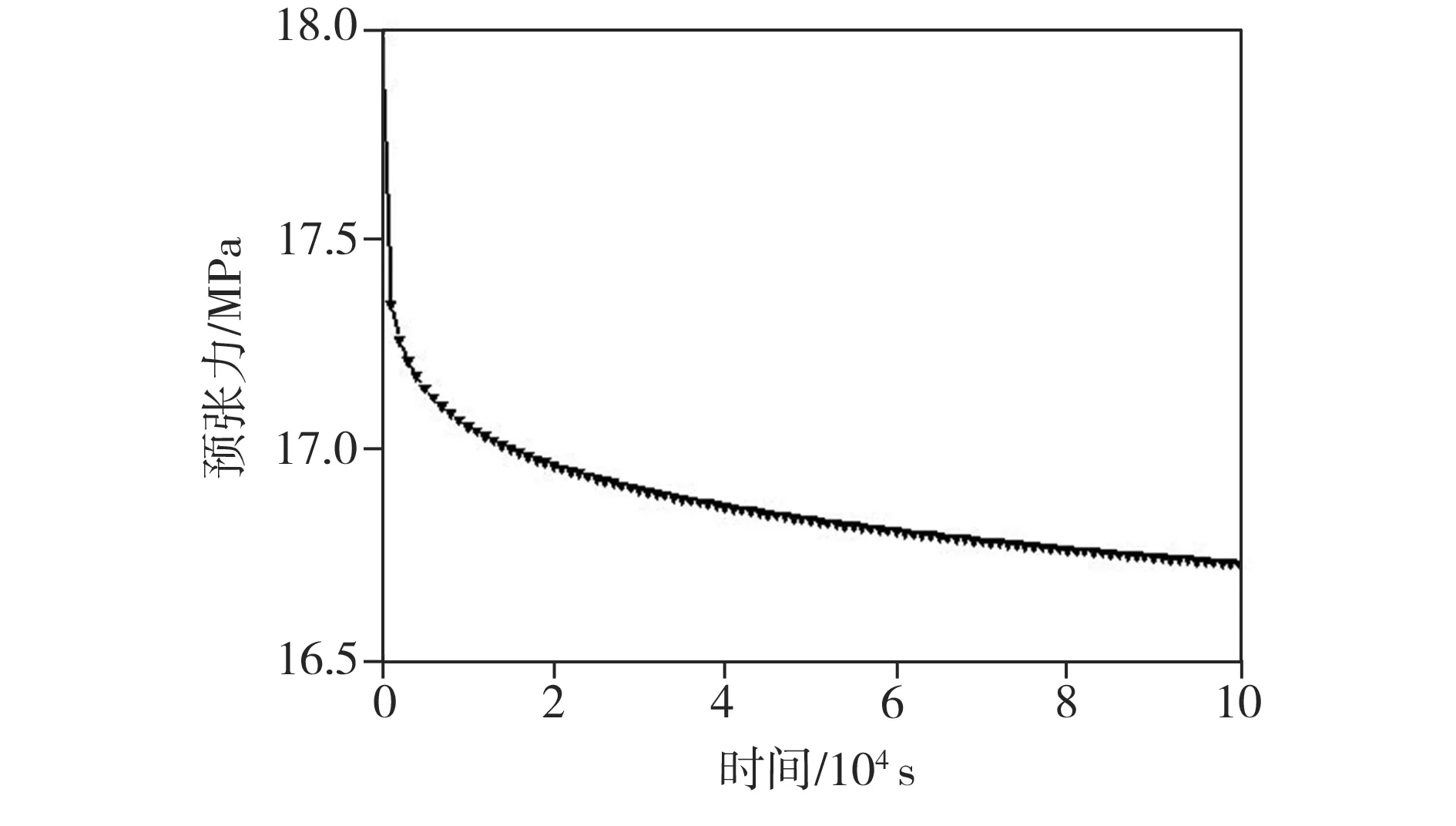
图3 预张力-时间曲线

设置不同初始预张力，在其余参数不变的条件下对工程实例进行仿真分析的结果如表1所示，从表1中可以看出，初始预张力越大，蠕变造成的膜结构预张力的衰减量越大，在初始预张力为6～18 MPa的条件下，蠕变105s时膜材的蠕变影响因子(即蠕变后膜材预张力与其初始值之比)为0.87～0.93。叶瑾瑜[5]对PTFE膜材进行了为期2年的蠕变试验，总结出PTFE的蠕变因子为0.813～0.874，经对比可以看出，本研究中膜材在105s内的蠕变因子已与其相差不大，因此蠕变试验只需进行1～2天就能基本反映出膜材长期的蠕变特性。

表1 不同预张力下的蠕变结果

3.2.2 均布载荷下膜面挠度与蠕变的关系

膜结构在室外环境中经常受风、雨、雪等环境载荷作用，在此类载荷长期作用下会使膜结构发生蠕变，最终导致破坏，因此找出膜结构在持续载荷下的蠕变规律至关重要。本文以膜面沿其法线方向的最大线位移量为膜面挠度，对膜面挠度变化进行ANSYS仿真分析，初始条件及载荷步设置与膜结构预张力仿真分析时相同，在膜面上分别加载200、500、1000 Pa三种均布载荷，分析结果如图4所示。从图4中可以看出，在三种载荷作用下，膜面挠度仅在初始阶段变化明显，随着时间的延长而趋于稳定，符合蠕变第一阶段特征。蠕变105s时，三种载荷对应的膜面挠度分别为10.60、25.90、48.45 mm，相比初始状态增加量依次为0.74、1.73、2.85 mm，表明载荷越大材料变形越明显。在最后的104s内，三种载荷作用下膜材蠕变的速率分别为1×10-6、2×10-6、4×10-6mm/s，这表明载荷越大，膜材稳态蠕变速率也越大，模结构更容易被破坏。

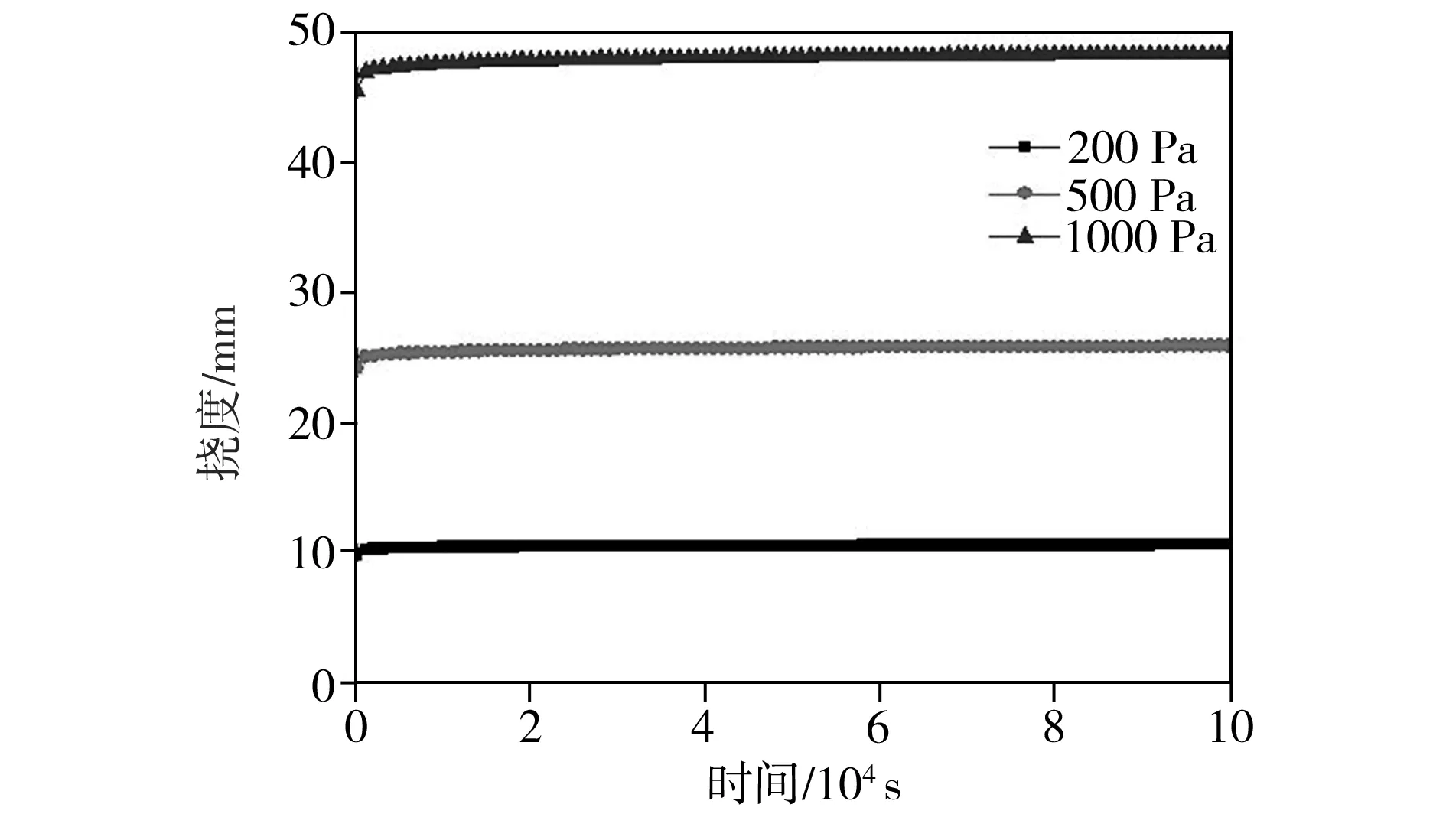
图4 不同载荷下的挠度-时间曲线

3.3 基于蠕变的理论计算

3.3.1 基于蠕变的膜结构预张力计算公式的推导

基于改进的时间硬化理论模型，采用欧拉法进行膜结构预张力理论计算公式的推导。将公式(1)看作自变量为t的函数，把整个时间段等分成若干区间，单个区间长度为h，时间节点设为t1，t2，…，tn，对应的材料应变和预张力分别为ε1，ε2，…，εn及σ1，σ2，…，σn，根据欧拉法计算可得

εn+1=εn+hε(tn,εn)

(2)

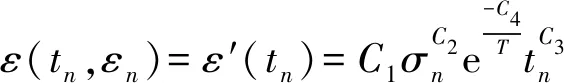
设ε0为施加预张力时的瞬间应变，则有

(3)

式中：σ0为膜结构初始预张力，MPa；E为膜材弹性模量，MPa。取t0=0，由式(2)和式(3)可以得到ε1、σ1的求解方程分别为

ε1=ε0+hε(t0,ε0)

(4)

σ1=σ0-E(ε1-ε0)

(5)

以此类推可求出ε2、σ2，ε3、σ3，…，εn、σn的求解方程分别为

ε2=ε1+hε(t1,ε1)

(6)

σ2=σ1-E(ε2-ε1)

(7)

⋮

εn=εn-1+hε(tn-1,εn-1)

(8)

σn=σn-1-E(εn-εn-1)

(9)

通过以上这种不断迭代的方式即可求出任一蠕变时间时膜结构的预张力。

3.3.2 均布载荷下基于蠕变的膜面挠度计算公式的推导

当膜面受到均布载荷作用时，膜面的挠度随着蠕变时间延长而逐渐增加，同样可利用欧拉法对其进行推导计算。平面膜结构的小挠度理论表达式为[8]

(10)

式中：w为膜面挠度，mm；q为均布载荷，MPa；H为膜材厚度，mm；σ0为初始预张力，MPa；a为膜材长度，mm；b为膜材宽度，mm。因膜面挠度较小，可把膜面变形后截面的弧线近似处理为直线段，示意图如图5所示。在推导膜面挠度计算公式前，首先根据式(10)计算出膜面初始挠度w0，则膜材长度和宽度方向的初始应变εa0、εb0分别为

(11)

(12)

相应方向的应力σa0、σb0分别为

(13)

(14)

然后根据式(2)可求出t1时刻膜材长度和宽度两个方向上的应变εa1、εb1分别为

εa1=εa0+hε(t0,εa0)

(15)

εb1=εb0+hε(t0,εb0)

(16)

相应方向上的应力σa1、σb1分别为

σa1=σa0+E(εa1-εa0)

(17)

σb1=σb0+E(εb1-εb0)

(18)

逐步递推，即可求出tn时刻膜材长度和宽度方向上的应变εan、εbn分别为：

εan=εan-1+hε(tn-1,εan-1)

(19)

εbn=εbn-1+hε(tn-1,εbn-1)

(20)

进而以长度或宽度方向的应变为变量，均可求出tn时刻膜面的挠度wn，求解方程式分别为

(21)

(22)

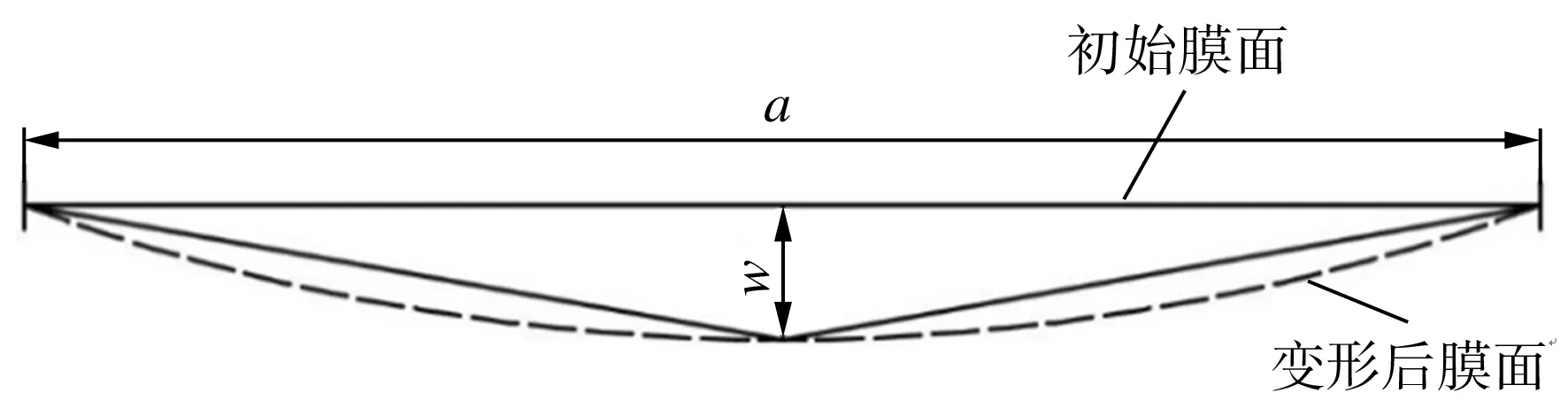
图5 膜面变形

将所推导理论公式运用于工程实例。按工程中预张力为18 MPa，均布载荷为1000 Pa，由公式(3)可计算出膜材初始瞬间应变为9.89×10-3，取h为103s，基于公式(8)和(9)并借助MATLAB软件进行循环迭代，可计算出蠕变105s时膜材的预张力值为16.04 MPa，与其ANSYS仿真所得相应值相差不大。同理，由公式(10)可计算出膜材初始膜面挠度为55.66 mm，基于公式(19)～(22) 并利用MATLAB软件进行迭代计算，可得出蠕变105s时膜面挠度为58.55 mm，与其ANSYS仿真所得相应值差别较大。

3.4 蠕变试验验证

针对膜结构蠕变分析，最简单经济的方法是借助有限元仿真，但有限元分析结果可能会与工程实际有所偏差，因此需要验证有限元分析的可靠性。搭建如图6所示的试验平台，膜材置于矩形框架上，其四周每隔300 mm布置一套拉紧装置，拉紧装置由花篮螺栓、U型环、传感器构成。由于膜材基材是经过平织法编织而成，初始时其内部纤维未能完全拉紧，需要反复张拉使膜材内部性能达到稳定。因此，试验开始前先将膜材安装在装置上预拉伸3次，每次拉力为18 MPa，保持1 h，然后进行试验。设置初始预张力为18 MPa，每隔103s记录一次数据，持续105s,得到的膜结构预张力变化曲线与其相应的仿真结果对比如图7所示。从图7中可以看出，试验和仿真曲线变化趋势大致相同，在最初的时间段，实际膜结构预张力下降幅度比其相应仿真结果略大，这是由于试验设备之间存在连接间隙，并且试验设备在拉伸时也会产生变形，这些因素都会使试验结果产生误差。膜结构实际蠕变105s时的预张力为16.43 MPa而相应仿真值为16.73 MPa，两者基本吻合，可以证明有限元分析结果的可靠性，这为工程中平面膜结构预张力的蠕变预测提供了方便可行的手段。受试验条件所限，本文未能进行膜面挠度测试。

图6 试验平台

图7 仿真和试验结果对比

4 结语

为了研究材料蠕变效应对平面膜结构稳定性的影响并给相关工程实际作业提供方便、准确的分析预测方法，本文针对工程实例，基于改进的时间硬化模型(MTHM)，借助ANSYS有限元分析软件及采用欧拉法自行推导的相关方程分别对膜材蠕变过程中平面膜结构预张力及膜面挠度的变化进行了模拟仿真及理论计算。结果表明，膜结构预张力及膜面挠度在膜材蠕变过程中的变化规律符合材料蠕变阶段典型特征，膜结构预张力的ANSYS模拟分析与理论计算分析结果相差不大，而膜面挠度理论计算值明显高于其相应的ANSYS模拟分析值。此外，本文还构建平台，实际进行了膜材的蠕变试验，所测得膜结构预张力试验值与其ANSYS模拟分析值基本吻合，表明该模拟方法分析结果可靠程度较高，能实际应用于平面膜结构稳定性分析预测，相关测试也间接验证了本文所采用的蠕变本构模型的合理性。但本文不足之处在于，MTHM模型只适用于分析材料短时蠕变，因此文中仅分析了105s内膜结构预张力的变化情况。在正常情况下，膜材蠕变在数年时间内的变化都很稳定，膜结构预张力最终会减小到一个定值，膜面变形也会趋于稳定，目前针对材料长期蠕变结果的研究只能通过加速材料蠕变的方法，即提高预张力或环境温度来实现。