三角形光晶格中的量子液滴
2022-10-09陈善桐蔡晓妍陈逸熙黎永耀
刘 彬,陈善桐,蔡晓妍,黎 枫,陈逸熙,黎永耀*
(1.佛山科学技术学院物理与光电工程学院,广东佛山 528225;2.佛山科学技术学院 粤港澳智能微纳光电技术联合实验室,广东佛山 528225)
玻色-爱因斯坦凝聚(Bose Einstein Condensates,简称BECs)的实验实现,为自局域态的稳定性及动力学特性的研究提供了理想平台[1-9]。众所周知,BEC 中三次非线性吸引相互作用的存在通常会使二维/三维自由空间中的非线性模式发生坍塌,因此如何在高维系统中获得稳定的非线性自局域态仍然是非线性科学研究的热点问题[9]。一般来说,最简单有效的解决方法是对三次非线性吸引相互作用进行修正,例如引入二次非线性、三次-五次的竞争型非线性、饱和非线性或非局域非线性等[10-13]。另一方面,通过引入自旋-轨道耦合效应也有助于获得稳定的非线性自局域模式,如稳定的物质波孤子[14-16]。
近年来,一种由李-黄-杨(LEE-HUANG-YANG,简称LHY)[17]修正项所描述的新型自局域态,即量子液滴被实验实现。其突破了高维系统中仅有吸引相互作用时不能形成稳定自局域态的限制。实验上最早由德国T.Pfau 教授团队在极性的玻色原子气体镝中观察到量子液滴的存在,随后西班牙光电科学研究所CABRERA 等人在混合两组分的钾原子气体中实现了具有各向同性结构的量子液滴[18-19],随后三维、二维和一维模型中的量子液滴被广泛研究[20-39]。
研究表明,光晶格中的BECs 为非线性自局域态及动力学的研究提供了一个理想的平台。在光晶格中,多种物质波孤子被研究,物质波孤子的形成与量子液滴的形成存在一定的物理相似性,因此在量子液滴的研究中引入光晶格有重要意义。近年来,ZHOU 等人研究了一维光晶格中的量子液滴动力学问题,结果表明晶格势对量子液滴的稳定性有影响[40];DONG 等人研究了光晶格中的多稳量子液滴[41];ZHENG 等人分别探究了二维周期势中onsite 和offsite 型晶格量子液滴[42]。相比于一维系统,高维光晶格具有更高的自由度,同时更有利于构造形式多样的光晶格结构,如三角形光晶格和蜂窝状晶格结构等[43-44]。此外,在高维模型中,还可以探究有趣的涡旋模式。目前,基于三角形光晶格的晶格量子液滴及其涡旋态仍未被研究。基于以上的研究背景,本文主要研究当横向囚禁尺度是窄囚禁条件时,三角形光晶格中的基态和涡旋态晶格量子液滴,详细地分析总粒子数对晶格量子液滴的影响。
1 模型
根据参考文献[42],当横向囚禁尺度是窄囚禁条件时,即有其横向尺度,其中a±和a⊥分别为两分量BECs 中各自组分的自排斥散射长度和横线囚禁尺度。此时,由LHY 修正项所描述的Gross-Pitaevskii(简称GP)方程可以简化为如下形式
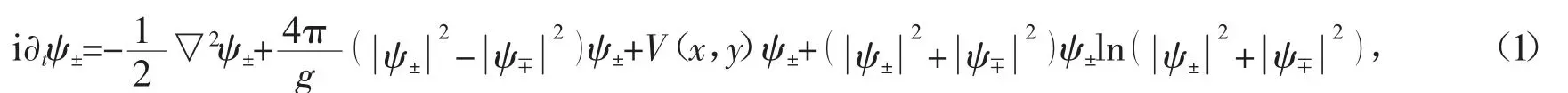
这里ψ±代表两组分波函数,g>0 表示耦合常数,V(x,y)表示三角形光晶格势。当横向囚禁尺度是窄囚禁条件时,LHY 修正项具有对数形式。进一步假设,当两组分BEC 满足对称条件时,即有方程(1)进一步简化为
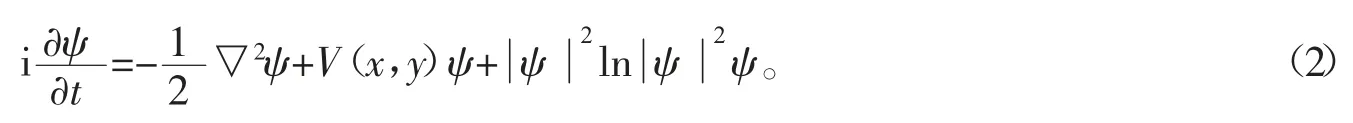
假设三角形光晶格势函数V(x,y)的具体表达形式为
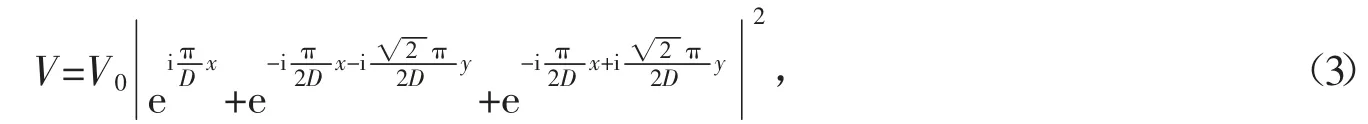
和
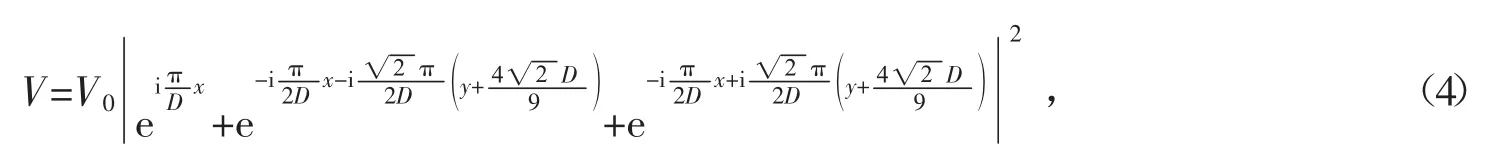

假设GP 方程具有如下形式的定态解

其中,φ(x,y)代表定态波函数,μ 为化学势。进一步假设初始定态波函数的形式如下

其中C 和α 是正实数,R 和θ 表示二维极坐标。该论文中采用虚时间方法[45]获得GP 方程(2)中的晶格量子液滴,并采用实时传输的方法进行稳定性验证;如果量子液滴的密度分布在整个实时传输的过程中保持不变,则说明晶格量子液滴是稳定的,反之则不稳定。
研究表明,在总粒子数足够大时,量子液滴具有“平顶型”分布的特征,此时记晶格量子液滴的峰值密度为。因此,晶格量子液滴的总面积可以表示为

进一步假设每个晶格的面积为s,晶格点数为n,则晶格量子液滴的总面积可以表示成A≈ns。表达式(8)可以进一步改写成

从表达式(9)可以看出晶格量子液滴占据的总格点数随着总粒子数的增加而增加。不失一般性,固定晶格周期D=1.2π 和晶格调制深度V0=-2 来研究总粒子数对晶格量子液滴的影响。
2 数值结果
2.1 S=0 的晶格量子液滴
图1 和图2 分别给出了两类典型的晶格量子液滴,即onsite 型和offsite 型晶格量子液滴。根据表达式(9),晶格量子液滴占据格点数随着总粒子数的增加而增加,但对于onsite 型和offsite 型晶格量子液滴其增加的方式不同。从图1 可以看出,对于onsite 型晶格量子液滴,其中心位于晶格点上,因此最小的占据格点数为n=1,如图1a 所示;接下来,向临近的6 个方向(每个方向之间的夹角均为60°)扩展,构成一个正六边形,此时占据总格点数目为n=7,如图1b 所示;随后,向次临近的方向扩充获得占据格点数n=13 的晶格量子液滴,如图1c 所示;随后补充临近位置获得n=19 的晶格量子液滴,如图1d 所示,此时再次回到正六边形情况;随后以大的正六边形为基础,向外扩展获得n=31 的晶格量子液滴,如图1e 所示。这里总粒子数依次为0.5、10、18、18 和40,分别对应图3a 中的a~e 点。
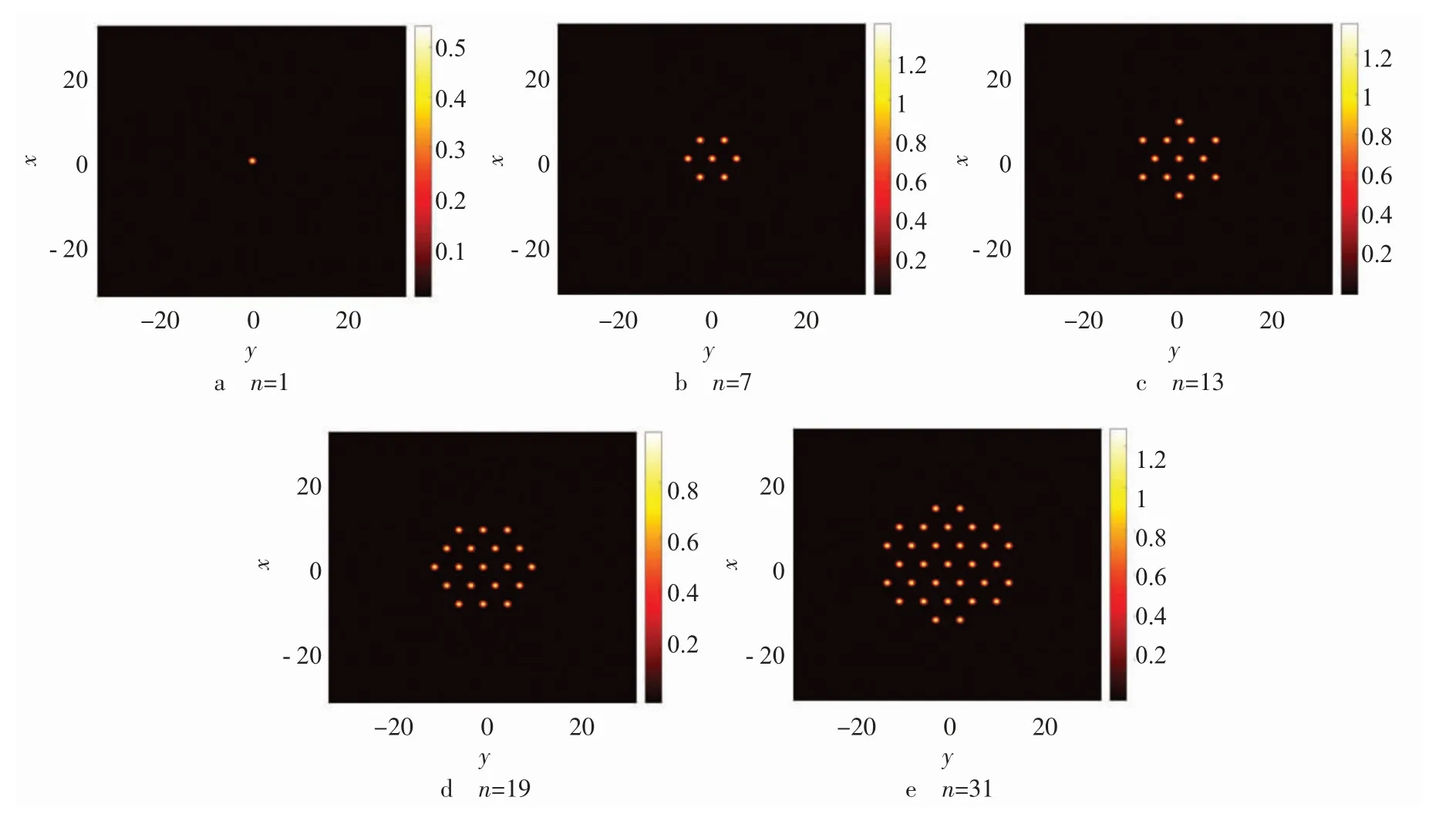
图1 S=0的onsite 型晶格量子液滴的密度分布图
对于offsite 型晶格量子液滴,由于中心不在晶格点上,因此最低的占据格点数是离坐标原点最近的3 个格点,即获得n=3 的晶格量子液滴,如图2a 所示;接着占据次临近的3 个格点获得n=6 的晶格量子液滴,如图2b 所示,构成一个正三角形;接下来以占据6 个晶格格点的晶格量子液滴为基础继续向外拓展,依次获得12、18 和21 的晶格量子液滴,如图2c~e 所示。值得注意的是,在第3 步到第5 步的增长过程中,因占据晶格格点所构成的形状并非正多边形,则下一步的扩展仅在所形成图形的长边方向进行扩展。图2 中总粒子数依次为3.9、6.9、13.5、17.7 和26,分别对应图3b 中的a~e 点。显然,基态的onsite 型晶格量子液滴的中心位于晶格点上;基态offsite 型晶格量子液滴的中心不在晶格点上;且在晶格调制深度固定的情况下,随着总粒子数的增加,晶格量子液滴占据的格点数随之增加。
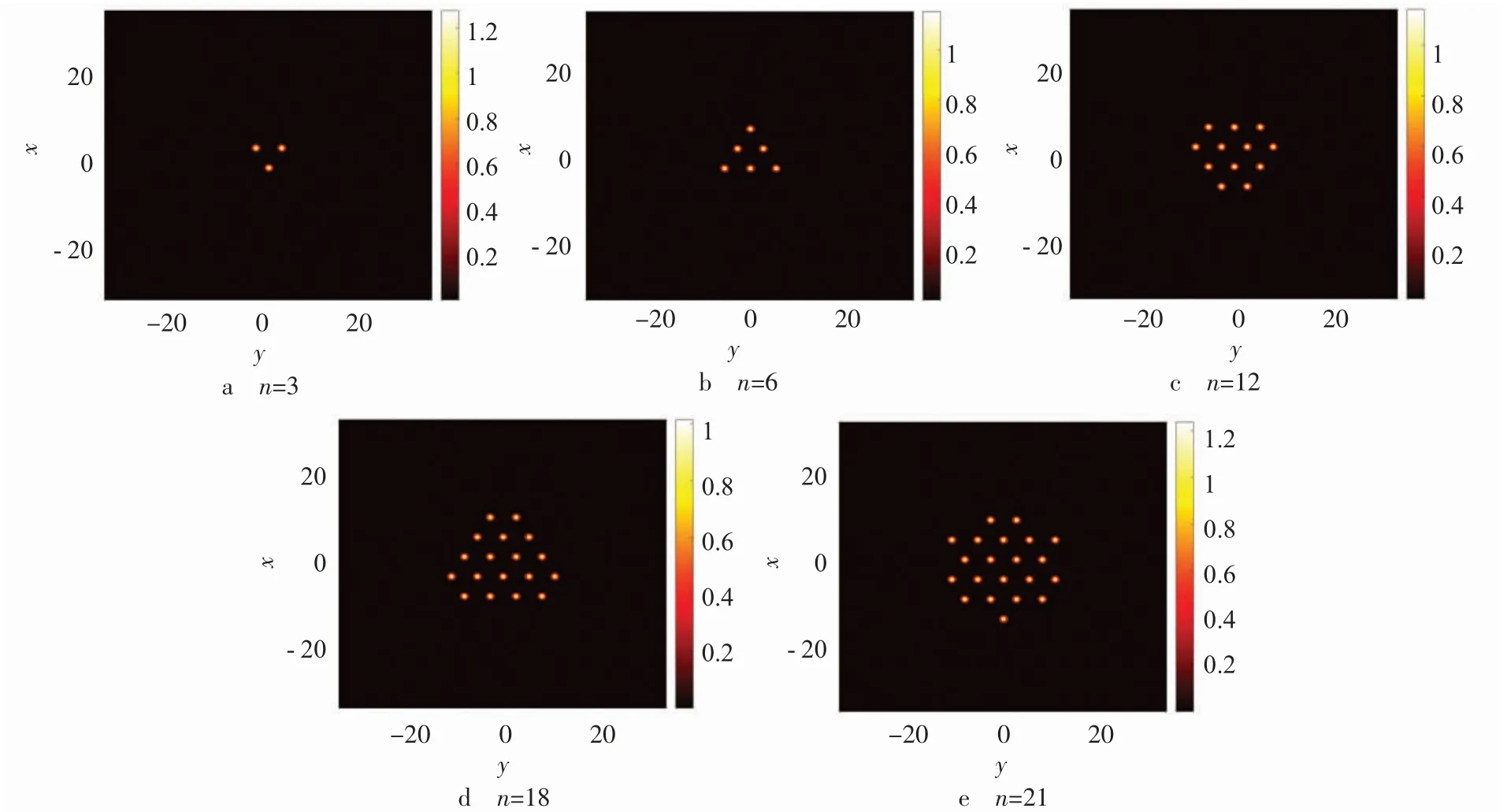
图2 S=0的offsite 型晶格量子液滴的密度分布图
接下来,详细给出S=0 时onsite 和offsite 型晶格量子液滴的μ-N 关系,如图3 所示。结果表明:一方面,无论是onsite 型晶格量子液滴还是offsite 型晶格量子液滴,仅在总粒子数较小时遵循Vakhitov-Kolokolov(VK)判据,一旦总粒子数超过一定值,则会出现违反VK 判据的情况,下面给出理论分析。
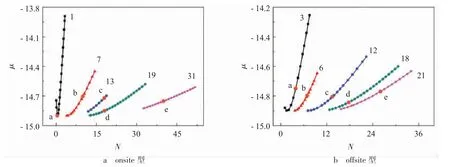
图3 S=0 的onsite 型与offsite 型晶格量子液滴的μ-N 关系图
进一步采用Thomas Fermi(TF)近似,结合表达式(8),可以获得化学势满足的方程

因此,若有N>A/e,则有dμ/dN>0,即出现违反VK 判据的情况。在数值模拟中,选择D=1.2π,此时每个晶格点占据的面积大约为2.786,此时临界的总粒子数大约为1.03,与数值结果基本一致。
另一方面,同一个N 值,可以对应不同的化学势μ 值,即获得占据不同格点数的晶格量子液滴,说明其有多稳的特性。图1b~c 展示了当N=18 时,分别占据13 点和19 点的onsite 型晶格量子液滴。同时,μ-N 关系图也展示了占据不同格点数的晶格量子液滴的稳定总粒子数范围。在这里,对稳定性的判定方式是在本征解上加入1%的随机扰动后进行实时传输演化的方式。图4 分别给出了31 点onsite 型和21 点offsite 型晶格量子液滴稳定传输的典型例子。
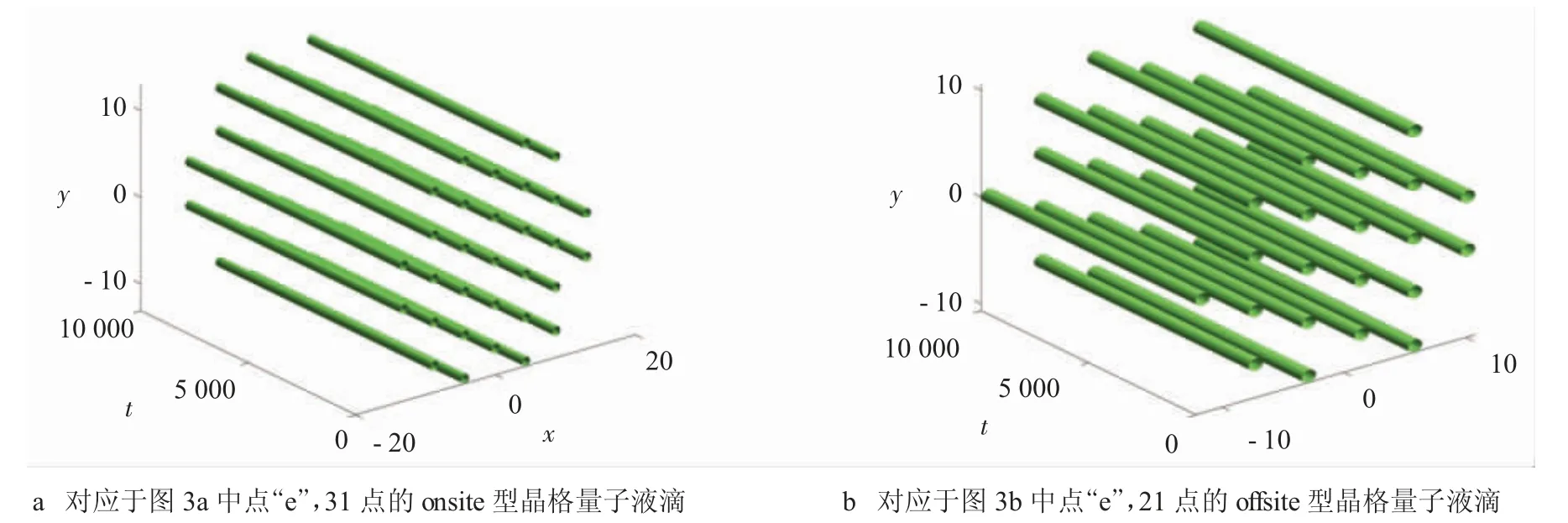
图4 晶格量子液滴稳定传输的典型例子
2.2 S=1 的涡旋晶格量子液滴
这里,将继续探究涡旋晶格量子液滴。与基态晶格量子液滴不同的是,涡旋量子液滴的中心被涡旋中心占据。因此,如图5 所示,对于onsite 型晶格涡旋量子液滴的扩展规律就像基态时的一样,但是中心被涡旋中心占据,故此时占据的格点数均为偶数;但是对offsite 型的涡旋晶格量子液滴的扩展规律不受影响,与基态时保持一致,如图6 所示。

图5 S=1的onsite 型晶格量子液滴的密度分布与相位分布图
图5 分别展示了拓扑荷S=1 时,占据6、12、18 和30 个晶格格点的onsite 型涡旋晶格量子液滴,其对应的总粒子数依次为6、13、18 和40。图6 分别展示了拓扑荷S=1 时占据3、6、12 和18 个晶格格点的offsite 型涡旋晶格量子液滴,其对应的总粒子数依次为4.5、9、9 和20。

图6 S=1的offsite 型晶格量子液滴的密度分布与相位分布图
可以看到,offsite 型晶格量子液滴的基态和涡旋态,因其占据相同的晶格点数而展示出同形异构的特点;且涡旋态中的onsite 型和offsite 型晶格量子液滴也会出现占据相同格点数目的情况,因此展示了完全异构的特性,图7 中的μ-N 关系图也很好地说明了这一特性。图7 展示了占据6 个晶格点和12 个晶格点的基态offsite 型、涡旋态onsite 型和涡旋态offsite 型晶格量子液滴的μ-N 关系,图中重合的区域显示相同的μ-N 值且占据相同数目的格点,但占据的方式是不同的,同一类型的晶格量子液滴之间展现出同形异构的特征,不同类型之间则展示出完全异构的特征。

图7 晶格量子液滴μ-N 关系图
3 结论
本文研究了当横向囚禁尺度是窄囚禁条件时,二维三角形光晶格中的晶格量子液滴。根据两类不同的三角形光晶格势,给出了基态和拓扑荷S=1 的涡旋晶格量子液滴的典型例子。如果晶格势的中心在晶格点上,则对应onsite 型晶格量子液滴;如果晶格势的中心不在晶格点上,则对应offsite 型晶格量子液滴。进一步详细地分析了两类晶格量子液滴占据格点数的扩展规律,通过μ-N 关系图,分别给出了每一类晶格量子液滴的稳定参数范围,一方面展现了晶格量子液滴的多稳特性;另一方面,若晶格量子液滴占据相同的晶格点数,则同类型之间展示出同形异构特征,不同类型之间展示完全异构的特征。本论文的研究结果,一方面可将其扩展到其他结构空间(如环形势)中量子液滴的研究,另一方面为双组分系统中隐秘涡旋量子液滴的研究提供基础。
