炭纤维复合材料应用于汽车后背门的设计与优化
2019-05-18戚振杰胡海欧崔世海霍俊焱
戚振杰,胡海欧,崔世海,霍俊焱
(1.天津科技大学机械工程学院,天津,300222;2.中国汽车技术研究中心有限公司汽车工程研究院,天津,300300)
纯电动汽车是当今以及未来的发展方向,轻量化是纯电动汽车发展的必然选择。对于纯电动汽车,在相同电池容量条件下,自身重量每降低40%则可减少40%的能量消耗,从而减少电池使用成本[1],因此减轻汽车重量是轻量化的核心目标。炭纤维复合材料具有许多金属材料无法比拟的优点,比如:密度低、比强度高、比模量大;材料性能具有可设计性;制品结构设计自由度大;抗腐蚀性强、耐久性能好、隔声降噪等,将其应用到汽车车身构件中不仅可以减轻质量,还具有抗冲击性能好的特点[2]。Lee等[3]采用尺寸优化、形状优化和拓扑优化等不同优化技术对复合材料结构进行分级优化,得到了理想的优化结果。洪清泉等[4]基于OptiStruct软件通过自由尺寸优化、尺寸优化和铺层次序优化等技术,在满足相关约束前提下,对复合材料结构进行不等厚设计,实现了复合材料厚度分布的最优化设计。文献[5-9]对炭纤维复合材料发动机罩均采用了新型的复合材料结构优化设计,既提高了其刚度、强度、模态频率等性能参数,又大大减轻了发动机罩的重量。
由于既要对炭纤维复合材料后背门进行CAE仿真分析,又要在满足其扭转刚度、弯曲刚度和侧向刚度以及一阶扭转和弯曲模态频率等多种性能参数的条件下对其进行三个阶段的优化[10],再加上后背门本身结构相对较复杂,因此设计难度较大。为此,本文以某SUV纯电动汽车的后背门为研究对象,利用有限元优化设计方法,以T300牌号炭纤维复合材料代替钢对汽车后背门进行轻量化的重新设计,通过自由尺寸优化、尺寸优化和铺层次序优化三个阶段对后背门炭纤维复合材料的铺层进行优化,并对优化后的炭纤维后背门各项性能参数进行分析,以期为炭纤维复合材料在汽车覆盖件上的应用提供参考。
1 钢制后背门的有限元分析
1.1 钢制后背门的有限元建模
所研究的SUV纯电动汽车后背门的质量为16.70 kg,应用CATIA软件对其进行三维实体建模。建模的重点在于后背门的内板和外板,而其他附件,比如加强板、铰链、发动机盖锁等次要部件对结果影响不大而作相应简化;另外,所研究汽车后背门的外板翻边纯属工艺要求范畴,对刚度以及模态频率影响极小,因此也予以忽略。划分网格时应满足单元的连续性、翘曲度、纵横比、雅阁比值和最大角及最小角等常数的要求,网格单元主体的基本尺寸为8 mm×8 mm 。后背门内、外板之间以及内外板与加强板之间的连接采用RBE2单元模拟刚性连接或螺栓连接,采用HyperMesh软件中的Adhesives方法模拟粘胶连接,内板和外板的连接方式在仿真时采用共节点的方式。所建立的钢制后背门有限元模型如图1所示,所用钢制件材料的性能参数如表1所示。

(a)外板
(b)内板
1.2 钢制后背门工况分析
根据文献[11-12]中对汽车后背门设计所采用的下垂刚度分析、扭转刚度分析、弯曲刚度分析等分析方法,并参照汽车车身设计的经验制定出汽车后背门各工况的边界条件如图2所示。从图2中可以看出后背门四种工况的边界条件,其中,红色三角位置是车身侧铰链安装孔的位置,黄色三角位置是后背门锁扣中心的位置,箭头指向位置是施加载荷点的位置,数字123456分别表示要约束的6个自由度。
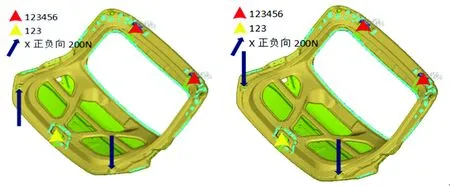
(a)扭转载荷工况
(b)弯曲载荷工况
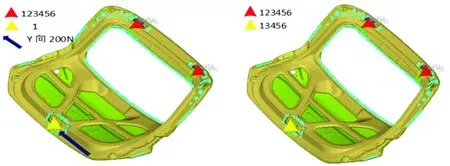
(c)侧向载荷工况
(d)约束模态
图2 后背门各工况的边界条件
Fig.2 Boundary conditions of back door under various working conditions
1.3 钢制后背门有限元仿真及实验验证
将钢制后背门有限元模型导入 HyperMesh软件中,加载上述四种工况所要求的约束以及载荷,然后进行静力学分析以及模态分析,得到钢制后背门的模态振型图如图3所示。从图3中可以看出,钢制后背门的一阶扭转模态频率、一阶弯曲模态频率分别为33.4、44.4 Hz,由此表明,钢制后背门的性能指标及仿真结果均满足企业的技术要求。
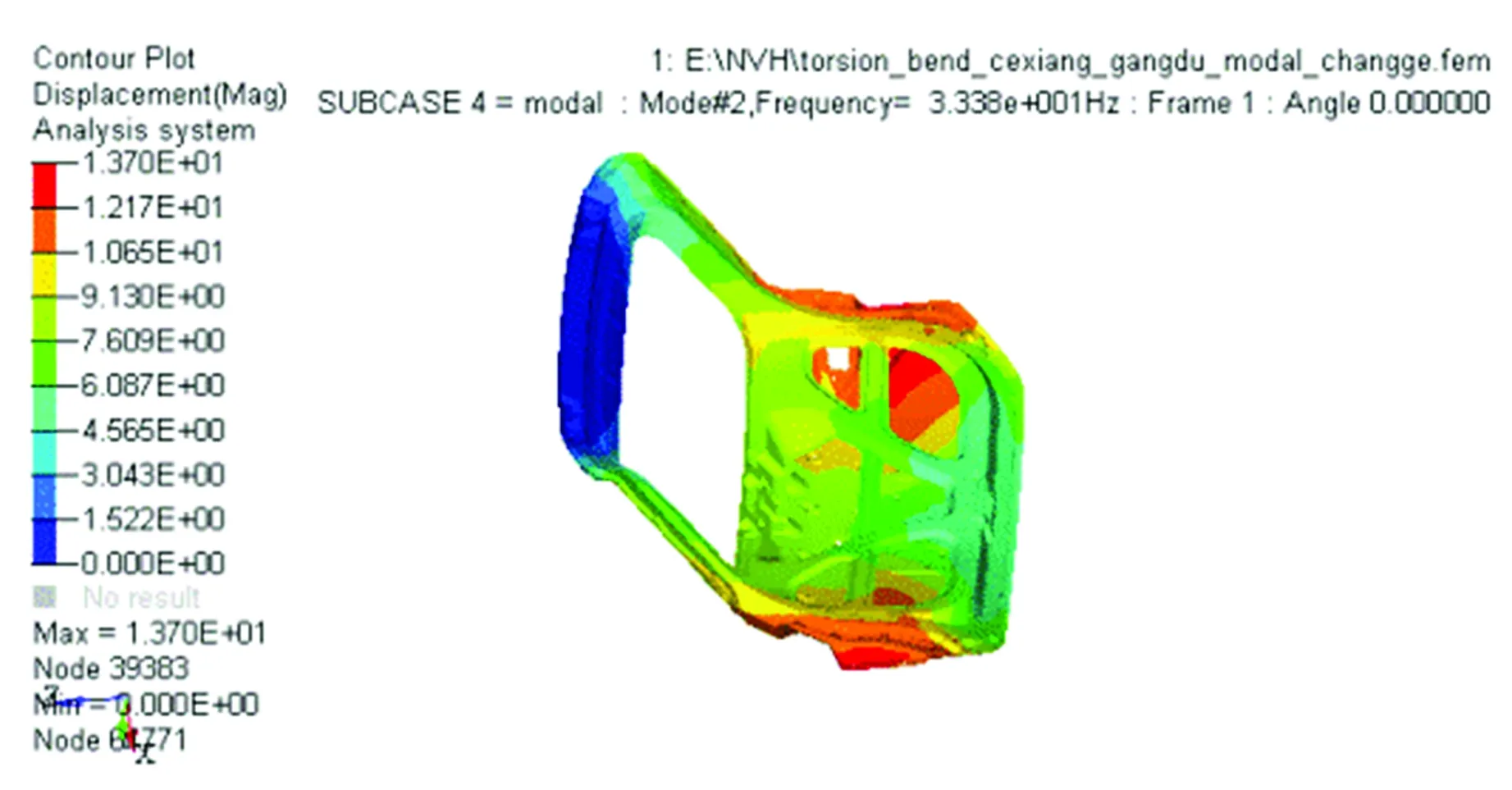
(a)扭转模态

(b)弯曲模态
由于炭纤维复合材料后背门的性能设计要以原钢制后背门为基础,因此要保证钢制后背门有限元仿真的精度。为了节省时间和成本,且钢制件有限元仿真精度已经得到业界的普遍认可,故本文只针对后背门的模态性能进行实验验证,钢制后背门性能的有限元仿真与实验结果对比如表2所示。从由表2中可以看出,钢制后背门的有限元仿真分析值和实验值基本吻合,满足其精度要求,验证了钢制后背门有限元建模方法的有效性。
表2 钢制后背门性能有限元仿真与实验结果对比
Table 2 Comparison between finite element simulation and test results of steel back door performance
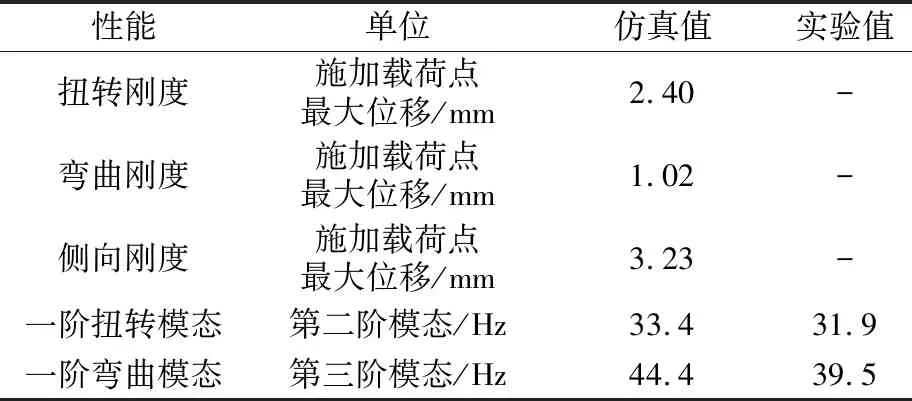
性能单位仿真值实验值扭转刚度施加载荷点最大位移/mm2.40-弯曲刚度施加载荷点最大位移/mm1.02-侧向刚度施加载荷点最大位移/mm3.23-一阶扭转模态第二阶模态/Hz33.431.9一阶弯曲模态第三阶模态/Hz44.439.5
2 炭纤维复合材料后背门优化设计
采用OptiStruct软件,围绕炭纤维复合材料后背门在各工况下的刚度、模态频率以及制造约束进行多层次优化设计。
2.1 材料选取
炭纤维复合材料种类众多,汽车工业中最常用的炭纤维牌号为 T300,T300牌号炭纤维材料有着优越的各项性能指标,而且产量高,具备一定的成本优势,在汽车工业以及其他相关产业有着广泛应用,因此本文选用T300牌号炭纤维材料,其性能参数如表3所示。

表3 T300 牌号炭纤维材料各项性能参数
2.2 优化原则
在进行优化时,遵循一般复合材料层合板设计的基本原则[13],有如下几种:
(1)平衡对称性设计。在设计时应尽量设计成均衡对称形式,避免层合板在固化后发生翘曲变形,第一,铺层中面对称; 第二,±45°角度铺层应成对铺设。具体为:[0°/45°/90°/45°/0°]=[0°/45°/90°]s,[45°/-45°/90°/0°/0°/90°/-45°/45°]=[45°/-45°/90°/0°]s。
(2)铺层方向(角度)设计。为提高工作效率,在满足受力的前提下,铺层方向数应尽量少,对要承受面内载荷的层合板应选择 0°、90°、±45°等4种铺层方向,±45°铺层应尽量靠近,以降低弯扭耦合。
(3)铺层顺序原则。应避免集中放置同一方向的铺层,而且最多不得超过4层; 对于层合板的最外部,应铺设±45°层,以改善层合板的抗压缩和抗冲击性能。
(4)综合考虑其最小铺层比例设计、最小铺层厚度设计以及变厚度(丢层)的设计。
2.3 自由尺寸优化
在设计过程中,为了既能获取制件最佳的材料分布形式和最优的整体厚度,又能减少设计变量以及简化优化过程,在原始铺层设计中将引入超级层的概念,把相同方向的每一个铺层叠加起来看作是一个加厚的铺层,即一个超级层,每一超级层原始厚度为0.5 mm。后背门内外板原始铺层设计如图4所示。从图4中可以看出,超级层一共含有0°、45°、-45°和90°四个角度铺层,这样就可以大大减少铺层数量,极大减少铺层角度、顺序和厚度等因素对自由尺寸优化结果的影响。在优化设计中以质量最小为优化目标,以静力学分析中钢制件的各性能指标为约束条件,同时还要考虑到以下相关的制造约束:(1)±45°角度平衡铺层;(2)层合板最小厚度约束为0.1 mm,最大厚度约束为2.4 mm;(3)最小和最大铺层厚度约束分别为层合板总厚度的20%和70%。
自由尺寸优化过程描述为:(1)优化设计变量:每个单元每一超级层的铺层厚度;(2)优化设计约束:扭转工况施加载荷点位移不大于2.40 mm,弯曲工况施加载荷点位移不大于1.02 mm,侧向工况施加载荷点位移不大于3.23 mm,内外板的体积分数不大于0.3;(3)优化设计目标:质量最小。
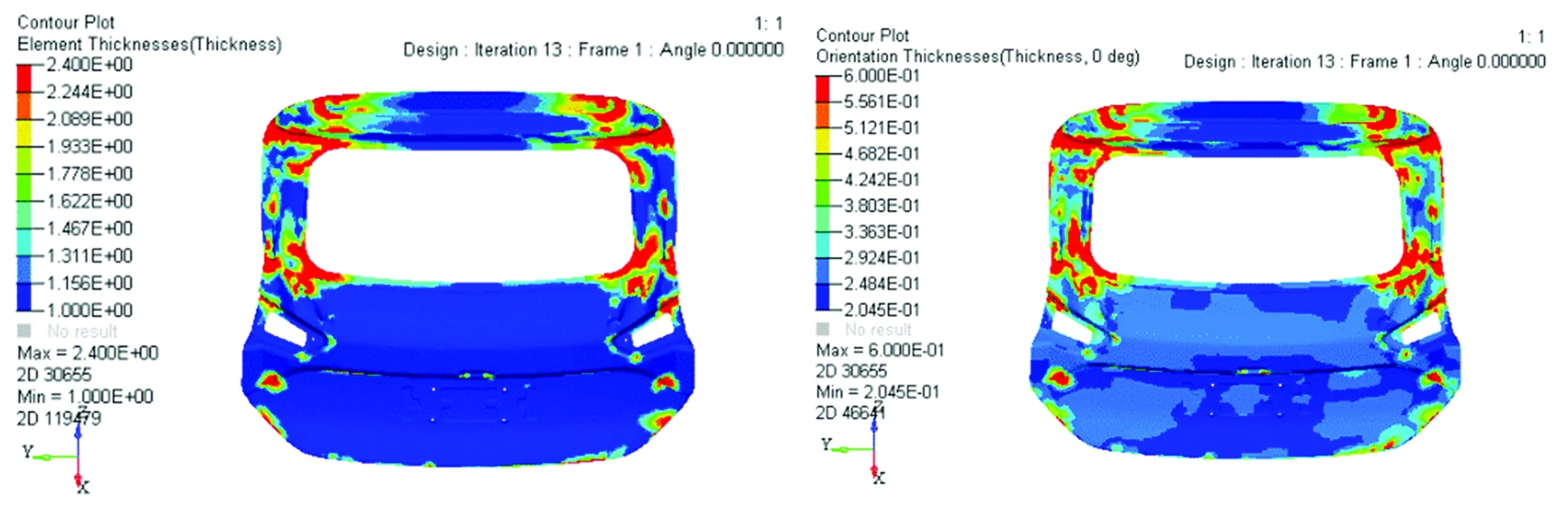
自由尺寸优化后,后背门外板和内板总体厚度分布和各角度铺层厚度的分布分别如图5和图6所示。由于±45°铺层厚度分布相同,故只展示45°铺层厚度分布。自由尺寸优化时后背门质量变化曲线如图7所示。从图7中可以看出,自由尺寸优化过程中,后背门的质量经过13次迭代后收敛,其质量由原来钢制件的16.70 kg降至8.03 kg,减重效果明显。
(a)总厚度
(b)0°

(c)45°
(d)90°
图5 自由尺寸优化后外板的总厚度分布和各角度铺层厚度分布
Fig.5 Total thickness distribution and lamination thickness distribution in different angles of
outer plate after free size optimization

(a)总厚度
(b)0°

(c)45°
(d)90°
图6 自由尺寸优化后内板的总厚度分布和各角度铺层厚度分布
Fig.6 Total thickness distribution and lamination thickness distribution in different anglesof inner plate after free size optimization
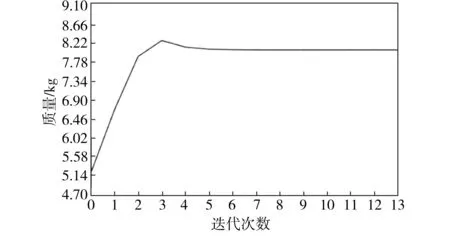
图7 自由尺寸优化时后背门质量变化曲线
Fig.7 Mass variation curve of back door during free size optimization
自由尺寸优化时各工况施加载荷点位移变化曲线如图8所示。从图8中可以看出,侧向载荷工况施加载荷点位移约束在3.23 mm后收敛,扭转载荷工况施加载荷点位移约束在2.40 mm后收敛,弯曲载荷工况施加载荷点位移约束在1.02 mm后收敛,由此表明,经过自由尺寸优化后,炭纤维后背门的扭转刚度、弯曲刚度和侧向刚度均达到钢制后背门的性能要求,而且其质量减少了51.9%。
由于每个角度的超级层厚度分布不均匀,因此可以采用不同形状铺层块叠加而成。在得到每
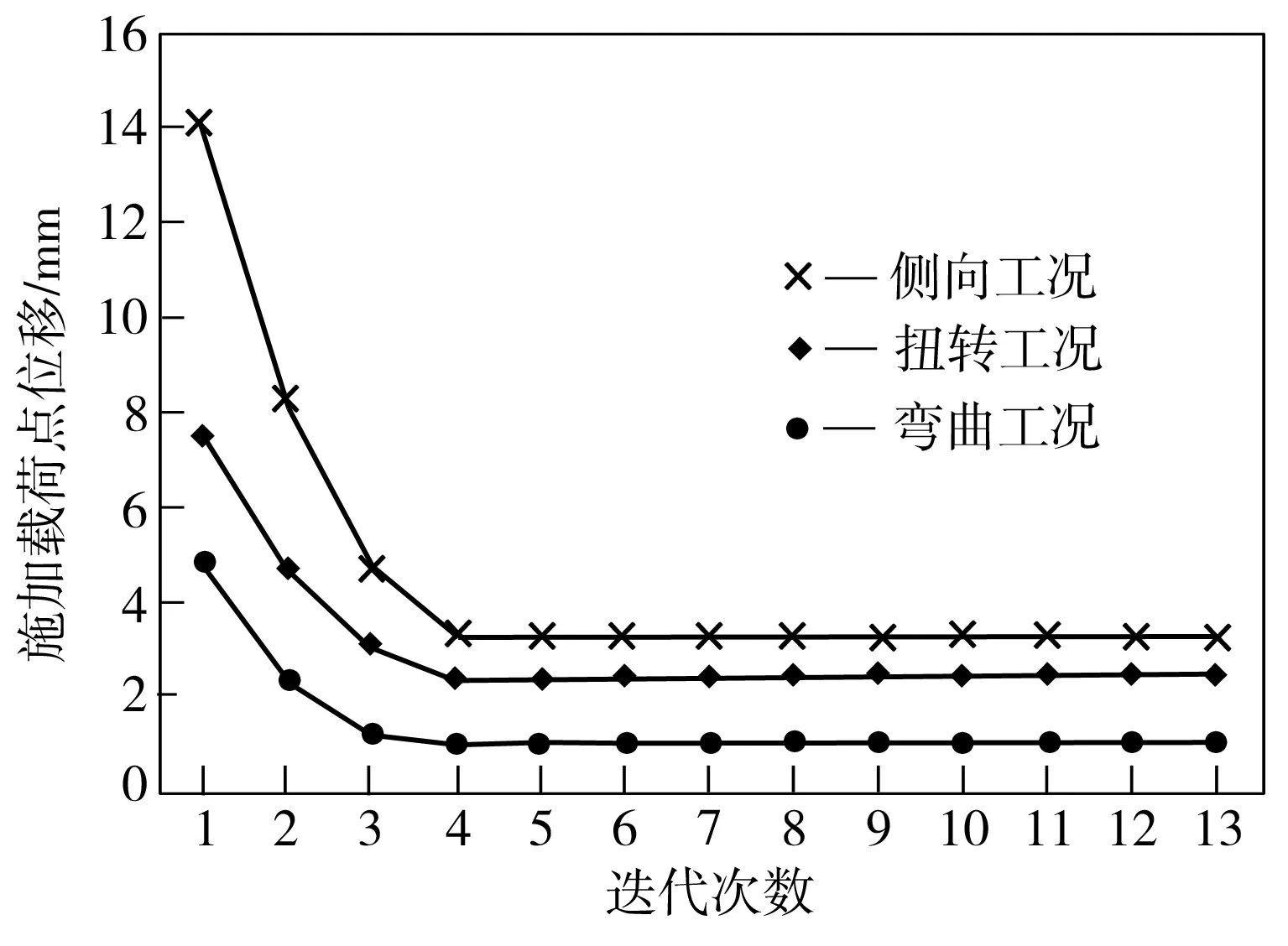
图8 自由尺寸优化时各工况施加载荷点位移变化曲线
Fig.8 Displacement curves of load applied points under each working condition during free size optimization
一单元每一超级层的最佳厚度后,利用OptiStruct软件,根据优化结果自动生成四个不同角度不同形状的铺层块,内外板铺层各形成16个铺层块,一共形成32个铺层块,每个铺层块代表着材料分布形状不同的若干铺层的集合,因此需要对各个铺层块进行解析并手动裁剪,使得最终各铺层的形状尽可能与优化结果保持一致,且满足实际制造的工艺要求,使之具有可制造性。后背门内外板铺层形状简化过程如图9所示。图9中展示了后背门外板0°方向第四个铺层块和后背门内板45°方向第二个铺层块的简化过程,左侧是自动生成的铺层块,右侧是手动裁剪后的铺层块,为下一步的尺寸优化做准备。

(a)外板0°方向第四铺层
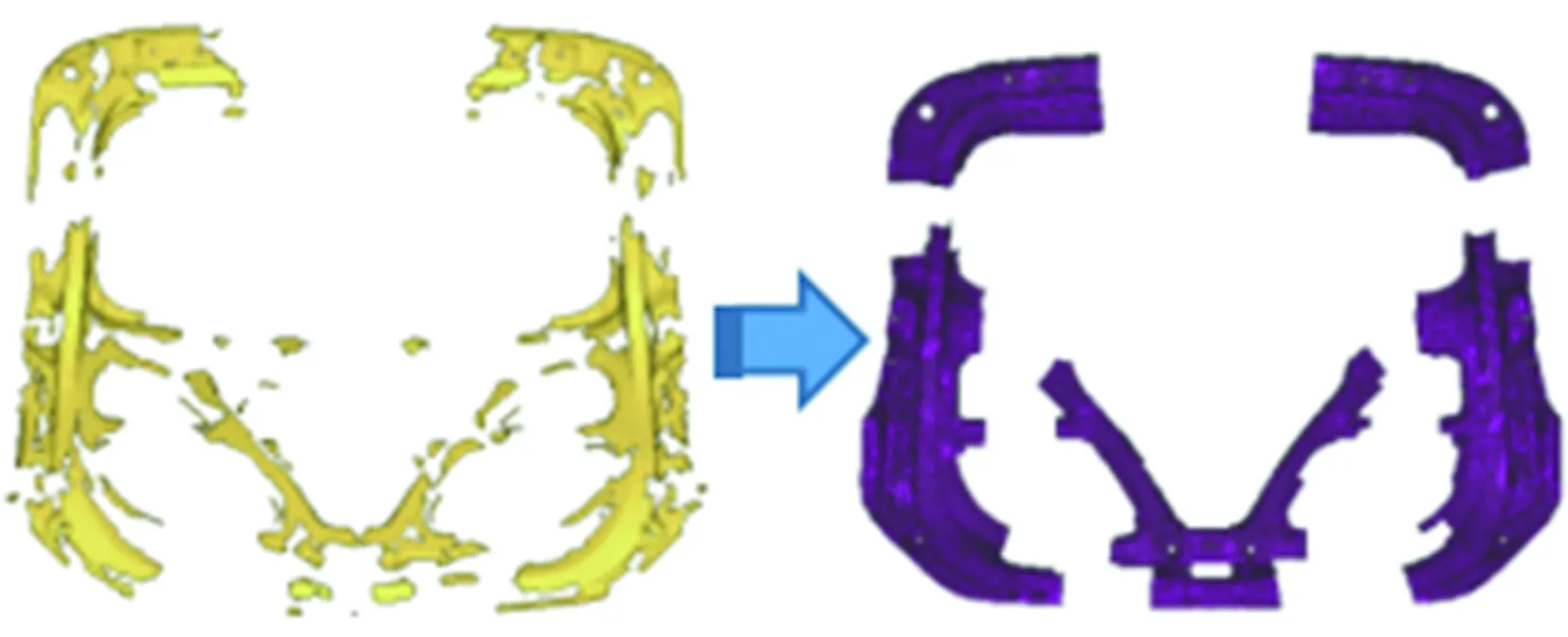
(b)内板45°方向第二铺层
Fig.9 Simplification process of the shape of inner and outer plates laminate of back door
2.4 尺寸优化
尺寸优化需要确定基本的铺层结构和各角度下的铺层数,此时,每一个铺层块的厚度都是一个设计变量。因此增加应力响应约束,其上下限值为±60 MPa,增加后背门扭转模态、弯曲模态频率约束,同时考虑到优化的基本原则和尺寸优化中的制造约束:将后背门内外板的层合板设置为对称优化;设置各铺层块的制造固化厚度均为0.1 mm。然后通过更新各个设计变量的上限值均为0.2 mm来最终确定后背门内外板中各方向的铺层数,也就得到了后背门内外板总的最佳尺寸。
尺寸优化过程描述为:(1)优化设计变量:每个形状铺层块的厚度;(2)优化设计约束:扭转工况施加载荷点位移不大于2.40 mm,弯曲工况施加载荷点位移不大于1.02 mm,侧向工况施加载荷点位移不大于3.23 mm,扭转模态频率不小于33.4 Hz,弯曲模态频率不小于44.4 Hz,复合材料应力介于-60~60 MPa之间;(3)优化设计目标:质量最小。
尺寸优化后后背门外板和内板的总厚度分布和各角度铺层厚度分布分别如图10和图11所示。
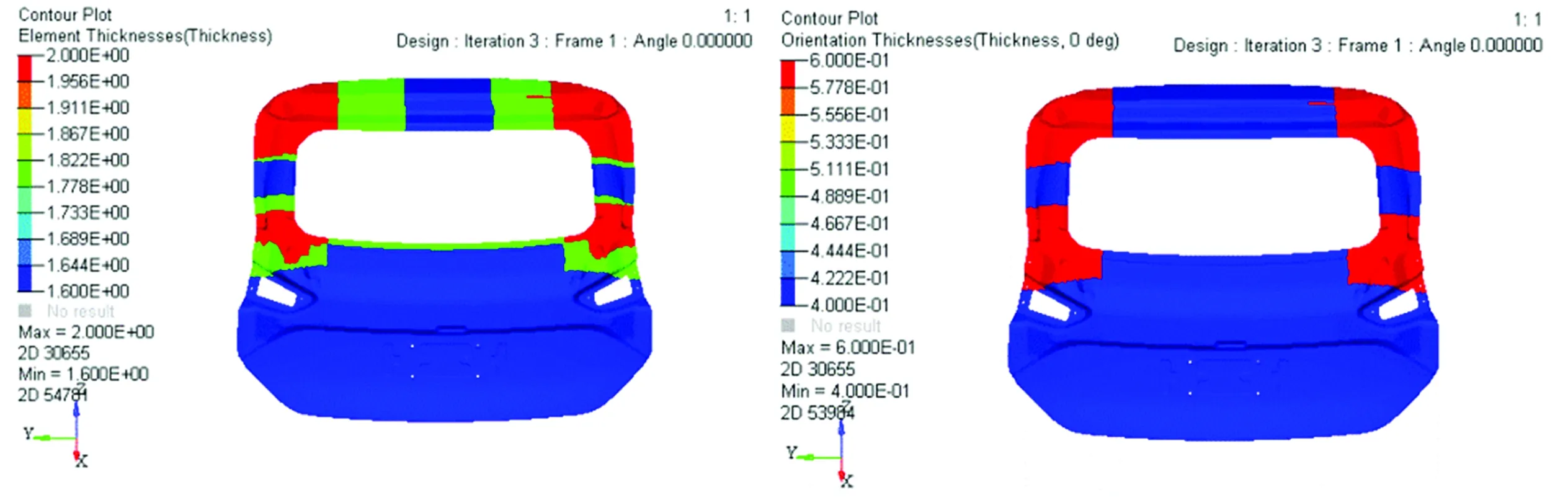
(a)总厚度
(b)0°

(c)45°
(d)90°
图10 尺寸优化后外板的总厚度分布和各角度铺层厚度分布
Fig.10 Total thickness distribution and lamination thickness distribution in different anglesof outer plate after size optimization
(a)总厚度
(b)0°

(c)45°
(d)90°
图11 尺寸优化后内板的总厚度分布和各角度铺层厚度分布
Fig.11 Total thickness distribution and lamination thickness distribution in different anglesof inner plate after size optimization
由于±45°铺层的厚度分布相同,故图10和图11中只展示了45°铺层厚度分布。
经过尺寸优化后,炭纤维后背门的模态频率迭代过程以及模态振型图如图12所示。从图12中可以看出,炭纤维后背门的一阶扭转模态频率经过3次迭代后收敛于48.8 Hz,一阶弯曲模态频率经过3次迭代后收敛于66.6 Hz,而钢制后背门的一阶扭转模态频率和一阶弯曲模态频率分别为33.4、44.4 Hz,由此表明,与钢制后背门相比,经过尺寸优化后,炭纤维后背门的一阶扭转模态频率和弯曲模态频率等性能均得到明显提高。

(a)扭转模态频率变化曲线
(b) 一阶扭转模态振型图

(c)弯曲模态频率变化曲线
(d) 一阶弯曲模态振型图
图12 尺寸优化后炭纤维后背门模态频率迭代过程以及模态振型图
Fig.12 Modal frequency iteration process and modal shape diagrams of carbon fiber back door after size optimization
尺寸优化前后后背门各项性能参数如表4所示。从表4中可以看出,经过尺寸优化后,后背门的质量由手动裁剪后的9.12 kg降至8.32 kg,减重0.8 kg;与钢制后背门相比,经过自由尺寸优化后,各工况施加载荷点最大位移不变,而经过尺寸优化后, 各工况施加载荷点最大位移均明显减小,由此表明,经过尺寸优化后,炭纤维后背门的扭转刚度、弯曲刚度和侧向刚度等性能得到明显提升。
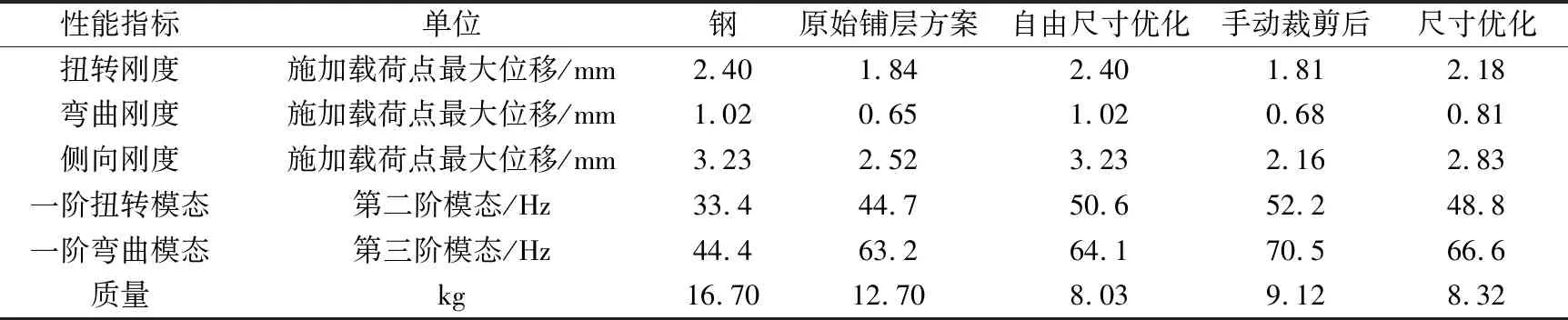
表4 尺寸优化前后后背门各项性能参数
2.5 铺层次序优化
炭纤维复合材料为正交各向异性材料,复合材料结构的整体性能随其铺层次序的变化而变化。针对复合材料这一特性,需要对铺层的层叠次序进行优化,使其满足复合材料的铺层规则,同时尽可能使其性能保持不变甚至得到提高。铺层次序优化是根据尺寸优化后的结果建立有限元模型再进行优化的。
铺层次序优化过程描述为:(1)优化设计变量为:后背门外板10层铺层的次序,内板9层铺层的次序,内外板设置为对称铺层;(2)优化设计约束:后背门内外板的外表面为±45°铺层,允许相同角度连续的最大铺层数为3;(3)优化设计目标:扭转工况、弯曲工况、侧向工况的加权柔度最小[13]。
经过4次迭代计算后,得到炭纤维后背门内外板铺层次序优化结果如图13所示。从图13中可以看出,后背门最终的外板铺层次序为[45°/-45°/45°/-45°/90°/90°/0°/0°/0°/90°]s,内板最终铺层次序为[45°/-45°/90°/45°/-45°/0°/0°/0°/90°]s。

(a)外板
(b)内板
图13 炭纤维后背门内外板铺层次序优化结果
Fig.13 Optimization results of lamination sequence of inner and outer plates of carbon fiber back door
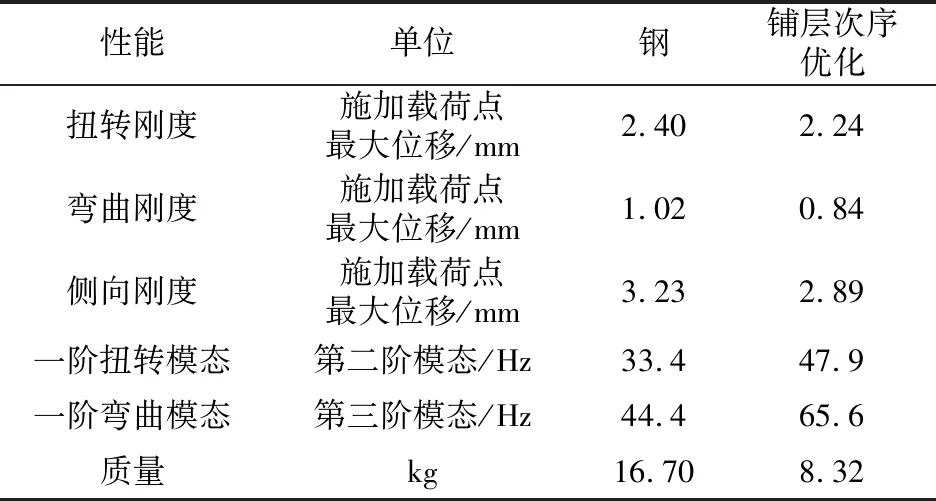
铺层次序优化后炭纤维后背门与原钢制后背门性能对比如表5所示。从表5中可以看出,优化后的炭纤维后背门与优化前的钢制后背门相比,其扭转刚度、弯曲刚度、侧向刚度、扭转模态频率、弯曲模态频率等性能均得到不同程度的提升,其中,一阶扭转模态频率由33.4 Hz提升至47.9 Hz,提高了43.4%;一阶弯曲模态频率由44.4Hz提升至65.6 Hz,提高了47.7%;扭转载荷工况、弯曲载荷工况以及侧向载荷工况施加载荷点的最大位移分别下降了6.7%、17.6%和10.5%,而且质量由原来的16.70 kg降至8.32 kg,减重率达到50.2%,轻量化效果明显。
表5 铺层次序优化后碳纤维后背门与原钢制后背门性能对比
Table 5 Performance comparison between post-lamination sequence optimization carbon fiber back door and original steel back door
性能单位钢铺层次序优化扭转刚度施加载荷点最大位移/mm2.402.24弯曲刚度施加载荷点最大位移/mm1.020.84侧向刚度施加载荷点最大位移/mm3.232.89一阶扭转模态第二阶模态/Hz33.447.9一阶弯曲模态第三阶模态/Hz44.465.6质量kg16.708.32
3 结语
(1)利用有限元优化设计方法,以T300牌号炭纤维复合材料代替钢对汽车后背门进行轻量化的重新设计,通过自由尺寸优化、尺寸优化和铺层次序优化三个阶段对后背门炭纤维复合材料的铺层进行优化。
(2)优化后的炭纤维后背门与优化前的钢制后背门相比,其扭转刚度、弯曲刚度、侧向刚度、扭转模态频率、弯曲模态频率等性能均得到不同程度的提升,其中,一阶扭转模态频率提高了43.4%;一阶弯曲模态提高了47.7%;扭转载荷工况、弯曲载荷工况以及侧向载荷工况施加载荷点的最大位移分别下降了6.7%、17.6%和10.5%;而且质量由原来的16.70 kg降至8.32 kg,减重率达50.2%,轻量化效果明显。
