基于扩展逐层法的复合材料层合板的自由振动

2019-05-14徐建新郭巧荣武耀罡

中国民航大学学报 2019年2期

徐建新，胥栋，郭巧荣，武耀罡

（中国民航大学航空工程学院，天津 300300）

航空器在长期服役过程中，复合材料结构不可避免地受到各种循环载荷作用，出现疲劳裂纹损伤。因此，分析含损伤复合材料结构的动力特性对提高安全水平具有重要意义。目前不含损伤的复合材料层合板自由振动分析的各种有限元模型已被国内外学者广泛研究[1-3]。王云洲等[4]建立了一种新的高阶位移模式，利用三阶剪切理论（TSDT）来分析边界条件、铺层等因素对复合材料层合板自振频率的影响。胡明勇等[5]基于Reddy分层理论（LWT）分析纤维体积含量和纤维增强厚度对复合材料层合板的自振频率和损耗因子的影响。Noor[6]使用经典层合板理论（CLPT）和一阶剪切理论（FSDT）对多分层复合材料层合板进行了自由振动分析，并与三维弹性理论（3D）结果相对比。对于四边简支层合板，Bert等[7]利用混合剪切板理论（HSDPT）提出一个封闭形式的解决方案。Owen等[8]基于分层理论建立一个改良模型用于预测无阻尼横向振动频率和屈曲荷载。Ghosh等[9]使用三阶剪切理论对四边简支反对称角度铺层矩形层合板进行了自由振动分析。

对于含裂纹梁的自由振动问题，许多学者也进行了研究，但对具有横向贯穿裂纹的复合材料板的自由振动研究较少。Kurtaran[10]研究了横向裂缝的各种参数对梁的固有频率的影响。Zheng等[11]提出了将总体附加柔度矩阵添加到相应完整梁单元的柔度矩阵中以获得总柔度矩阵的有限元方法。Kisa等[12]基于模态法构建了用于分析截面为圆形的阶梯裂纹梁的自由振动问题的有限元方法。Mogal[13]研究了具有两个开口横向裂纹悬臂梁的自由振动和响应特性。Liu等[14]在假设裂纹沿着梁的宽度呈直线分布的情况下，提出了新裂纹模型来研究具有斜裂纹悬臂梁的振动。

基于以上研究发现：经典层合板的横向剪切应变εXZ=εYZ=εZZ=0，此理论不适用于高各向异性比的复合材料结构，结果不精确且参考价值较小；一阶剪切理论的准确性取决于剪切修正系数，但通常很难实现且无法预测层间应力的分布，难以反映复合材料层合板的变形；高阶剪切理论不满足层间应力的连续性，也无法准确预测出层间应力；分层理论则在每层分别独立假设位移场，满足了层间位移连续条件，其计算结果精确，但不能计算含损伤结构。扩展逐层法[15-19]（XLWM,extended layerwise method）结合分层理论和扩展有限元方法（XFEM,extended finite element method）的优点，建立了含多层分层和基体裂纹损伤复合材料层合结构的扩展逐层理论。复合材料层合结构的扩展逐层理论能同时精确描述多层分层和多处基体裂纹损伤情况，拓展了扩展有限元方法在复合材料结构损伤分析和预测问题上的应用范围，能精确分析分层前缘和裂纹尖端的位移场和应力场。下面主要使用扩展逐层法研究含基体裂纹的复合材料层合板的自由振动问题。

1 扩展逐层理论

1.1 位移假设模式

含多层分层损伤的复合材料层合板沿厚度方向上的位移假设模式[15-19]如下

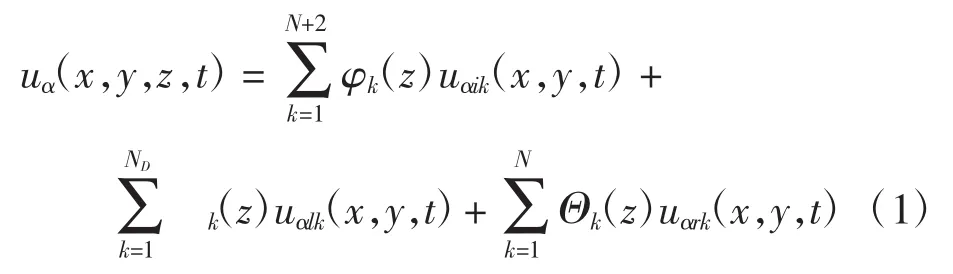
其中：α =1，2，3 表示位移在 x、y、z 3 个方向上的分量；i、l、r分别为标准自由度、由于分层损伤导致位移不连续扩充的附加自由度和层间界面导致的应变不连续扩充的附加自由度；k为厚度方向上每层层间和上下面上插值点的编号。

根据Einstein求和约定，式（1）可简化为

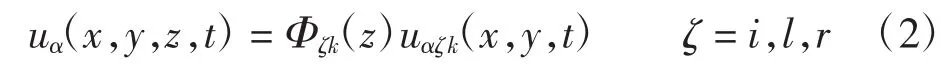
其中：Φik（z）=φk（z）为复合材料层合板结构在厚度方向上的线性拉格朗日插值函数；Φlk（z）=k（z）=φk（z）×Hk（z）是用来模拟分层损伤的强不连续函数，Hk（z）是一维Heaviside函数；Φrk（z）=Θk（z）=φk（z）χk（z）是用来模拟层间界面弱不连续函数，χk（z）是一维符号距离函数。如果在厚度方向上无分层损伤，位移场可简化为

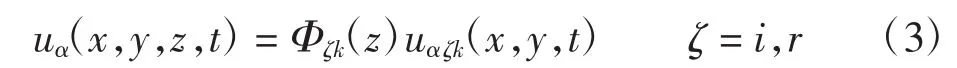
为了模拟平面内的横向基体裂纹，则需在位移场中引入扩充自由度来描述裂纹，面内位移基于扩展有限元方法可离散为

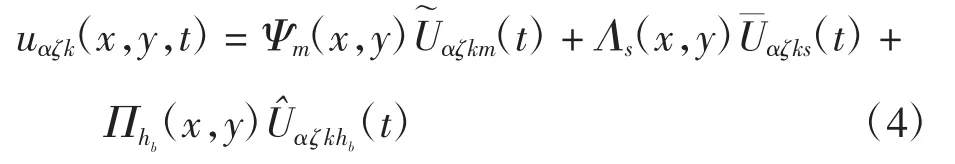
其中：m=1，2，…，NE，NE为面内有限元单元节点数；s=1，2，…为裂纹间断面扩充的节点数；h=1，2，为裂纹尖端的应力场而扩充的节点数；b=1，2，…，NF，NF为裂纹尖端而需扩充函数的数量；Ψm（x，y）为二维拉格朗日插值函数；Λs（x，y）=Ψs（x，y）×为描述裂纹面间断而扩充的形函数，FHs（x，y）是Heaviside函数；Πh（bx，y）=Ψ（hx，y）Fh（bx，y）为裂纹尖端的扩充函数，Fh（bx，y）为分支函数为标准自由度;为裂纹间断面引起的扩充自由度；为描述裂纹尖端引起的扩充自由度。

如果复合材料层合板不存在面内横向基体裂纹，则面内位移进行离散时不需引入扩充自由度，式（4）可写为

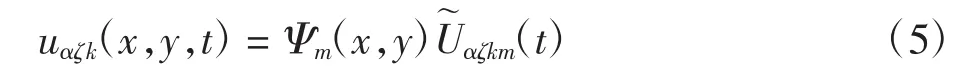
1.2 控制方程

利用哈密顿原理可得出复合材料层合板自由振动的控制方程。对于动态问题，控制方程如下

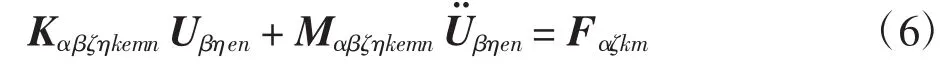
其中：Kαβζηkemn为单元刚度矩阵；Mαβζηkemn为单元质量矩阵，即

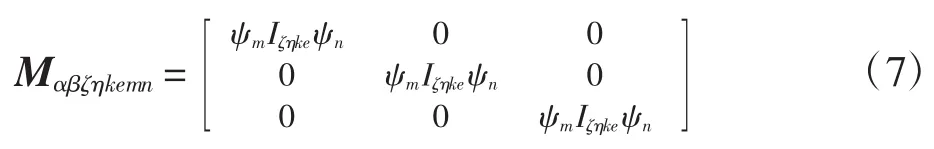
其中

对于含裂纹复合材料层合板，控制方程为

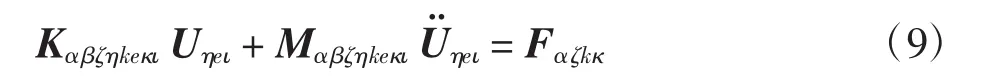
其中：ζ=i，r；κ=m，s，hb；ι=n，g，fb；m，n=1，2，…，NE；s，g=1，2，…，b=1，2，3，4。

单元总刚矩阵为

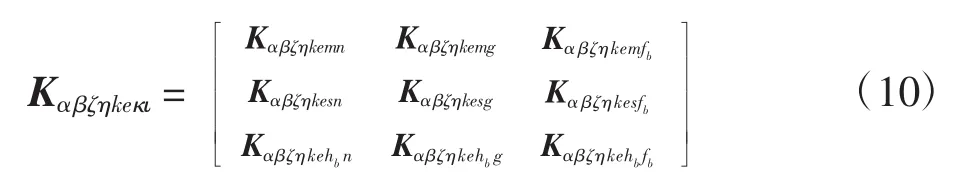
式中，Kαβζηkemn是不存在横向裂纹时的单元刚度矩阵，可表示为

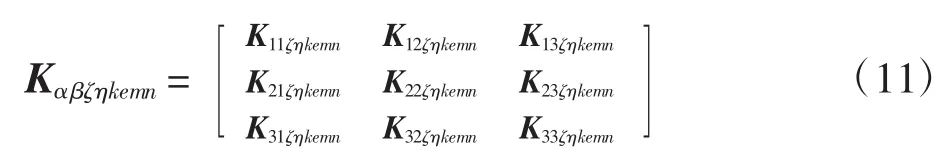
其中

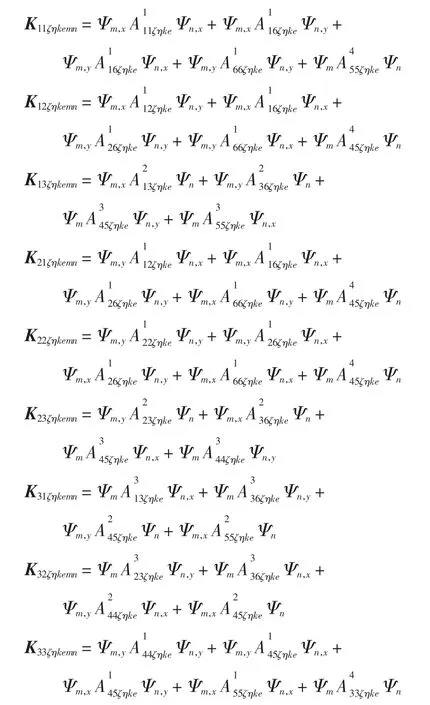
单元总质量矩阵为

式中，单元质量矩阵的子矩阵Mαβζηkesn可表示为

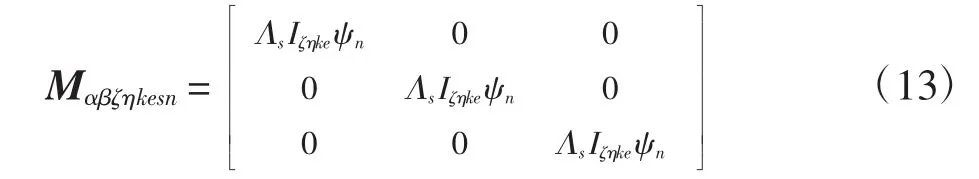
在自由振动分析中，复合材料层合板不受外力，则Fαζkm=0，令Uβηen（t）=φβηensin（ωt+θ），则

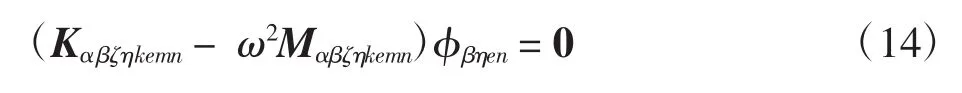
或

式中，Φ =[φ1，φ2，…，φn]是特征向量矩阵；Λ =diag[ω12，ω22，…，ωn2]是特征值矩阵。

2 研究算例

为便于计算与对比，以下均采用无量纲化固有频率 λ =10ω（ρh2/ET）1/2。设对称和反对称铺层的复合材料层合板厚度相同，每个单层的厚度因铺层数量的不同而不同。以单向纤维增强复合材料层合板为研究对象，研究无损伤和含基体裂纹复合材料层合板的无阻尼自由振动，并采用两种无量纲化的材料参数，如下：

1）材料Ⅰ

G12/E2=0.5 G23/E2=0.2

2）材料Ⅱ

G12/E2=0.6 G23/E2=0.5

这两种复合材料其他材料参数一致，μ12=μ13=0.25，ρ=1.0，G13=G12。

2.1 无损伤复合材料层合板

基频计算值会随网格密度增加而逐渐减小，只有达到收敛后计算结果与文献对比才有意义。首先以无损伤单向增强复合材料层合板为研究对象，研究不同铺层条件下，自由振动问题的收敛性。其余数值算例都采用达到收敛的网格划分密度。

研究对象为四边简支复合材料层合板。图1采用复合材料层合板的几何尺寸为：长宽比a/b=1.0，厚度和边长比h/a=0.2，铺层顺序为[0/90/0/90]。为研究多种情况下的收敛性问题，表1采用材料的几何尺寸为：a/b=1.0，h/a=0.1，铺层顺序为 [0/90]、[30/-30]、[45/-45]3种。在图1和表1的数值算例中，其边长上的网格节点数线性增加。

由图1可知，两种材料随着网格数量的增加，自由振动的无量纲固有频率逐渐降低，当网格达到30×30时，曲线趋于平稳。由表1可知，当网格数量为31×31和41×41，其无量纲固有频率仅发生微量变化，因此网格数为30×30时，无量纲固有频率收敛。

以无损伤复合材料层合板为研究对象，计算四边简支对称和反对称铺层复合材料层合板的无量纲化基频。无损伤复合材料层合板的几何尺寸、边界条件与图1算例一致，对称和反对称铺层的复合材料层合板有相同的厚度，每个单层的厚度因铺层数量的不同而不同，单层的材料属性为材料Ⅰ，各向异性度（E1/E2）从3～40变动，复合材料层合板模型网格数量为35×35。

将结果与文献[6，8-9]的结果对比，并以三维实体元模型（3D model）在MSC.Natran中求解结果作为参考，证明XLWM求解自由振动问题的精确性。

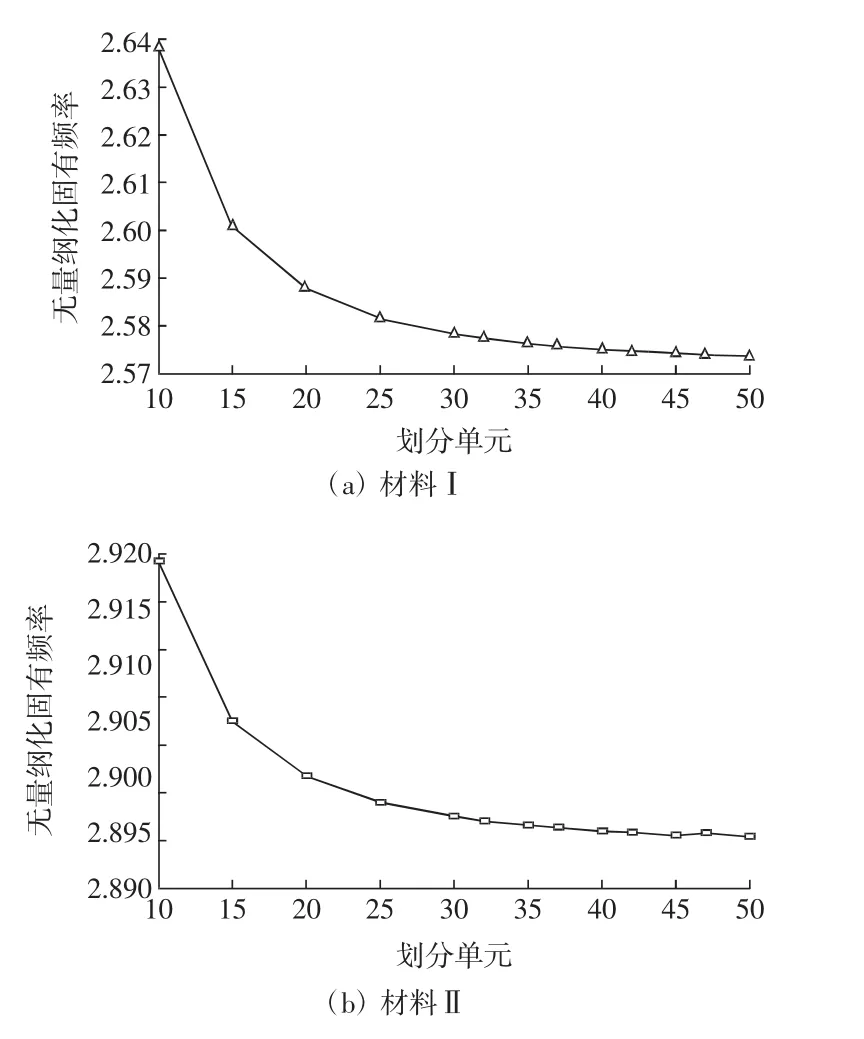
图1 铺层为[0/90/0/90]的复合材料层合板的收敛曲线Fig.1 Convergence curves of composite plate with stacking sequence[0/90/0/90]

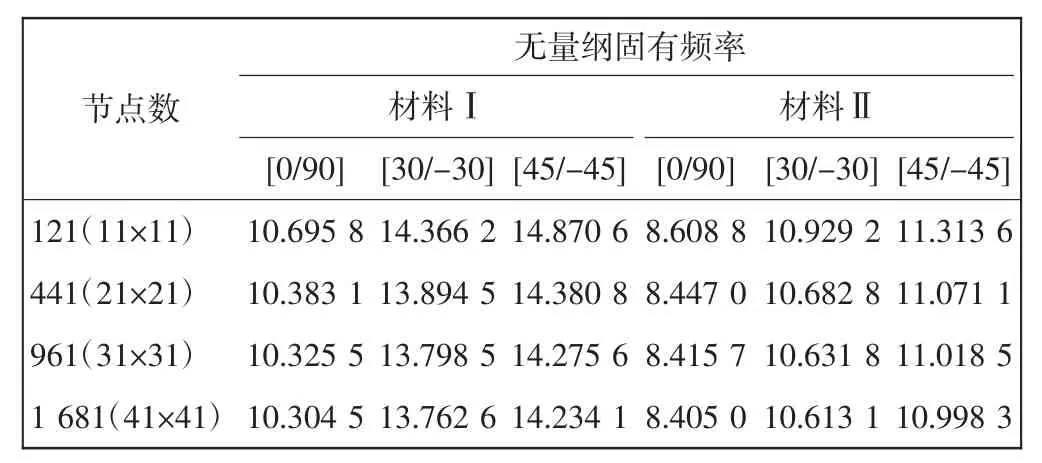
表1 节点数对无量纲固有频率的影响Tab.1 Effect of finite element mesh refinement on dimensionless fundamental frequency

在目前已提出的扩展逐层理论中，横向裂纹的裂纹面和裂纹尖端可由形函数Λs和Πhb进行模拟。而在三维实体元模型中，节点的不连续性由重复节点来描述。部分数据由于（E2/E1）1/2≤v12导致无法计算，所以只给出部分结果作为参考。

由表2可知：XLWM和三维实体元模型的结果最接近；当E1/E2逐渐增大时，和经典层合板理论的差距逐渐增大；当等厚度的复合材料层合板铺层数量增加且E1/E2增加时，相应的固有频率值，从35.8%增加到71.8%，说明复合材料层合板的铺层数量和各向异性度对固有频率影响显著。

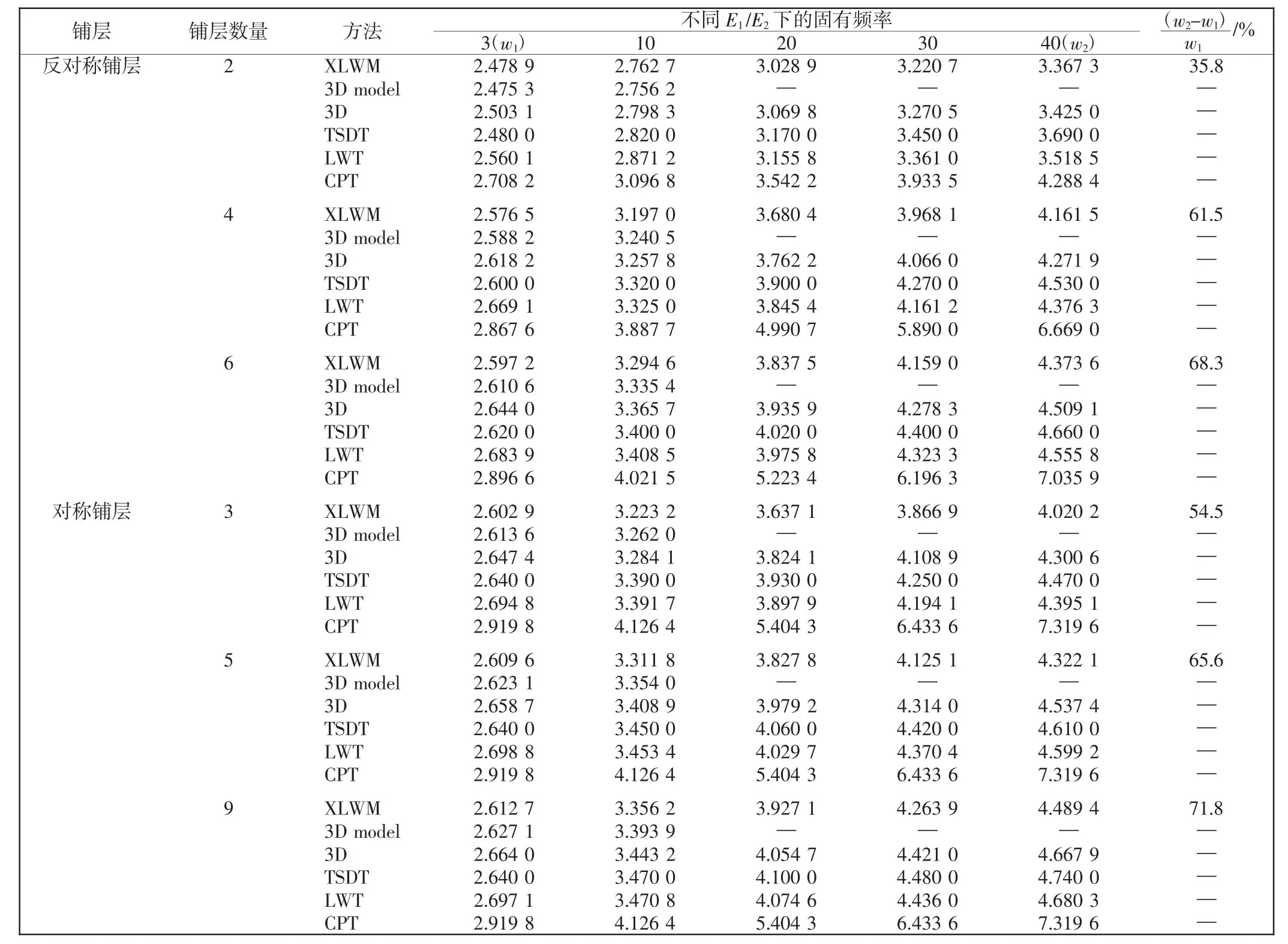
表2 不同方法中正交各向异性度与铺层数量对固有频率的影响Tab.2 Effect of orthotropic degree on fundamental frequency for simply supported square composite plates

2.2 含横向裂纹复合材料层合板

基于XLWM应用于无损伤复合材料层合板自由振动问题的正确性，研究含有基体裂纹情况下的复合材料层合板的振动特性，含中心贯穿裂纹复合材料层合板如图2所示。此研究模型尺寸为：a/b=1.0，h/a=0.2，边界条件为四边简支，材料参数为材料I（E1/E2=3），网格划分 37 × 37，裂纹长度（L/a）从 0～0.3逐渐增加。

以含中心裂纹的复合材料层合板为研究对象，研究铺层数量及裂纹长度对复合材料层合板固有频率的影响，并以无裂纹情况下的固有频率作为参考。将XLWM结果与三维实体元结果相对比，证明其准确性。

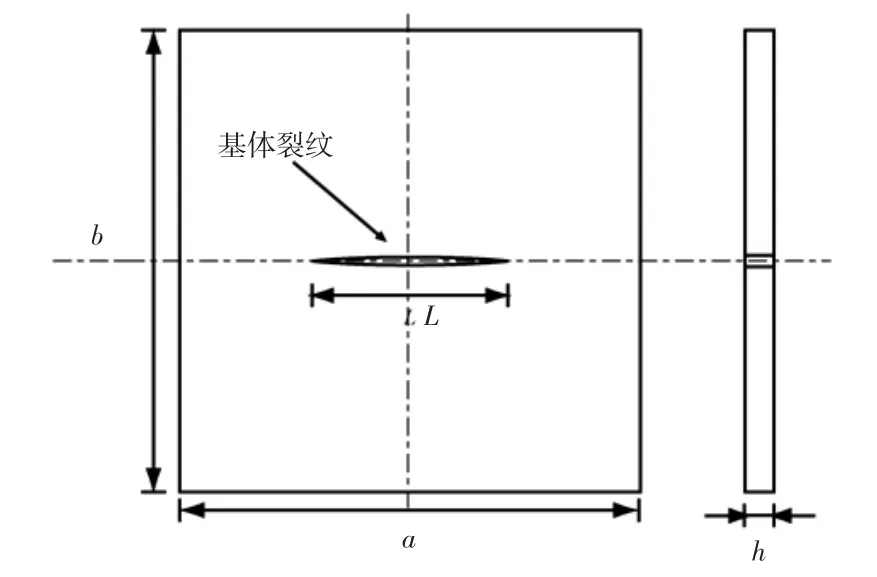
图2 含中心贯穿裂纹的复合材料层合板Fig.2 Composite laminates with central penetrating cracks

由表3可知：中心裂纹长度对对称铺层和反对称铺层复合材料层合板的固有频率影响一致；当铺层数不变，裂纹长度增加时，固有频率减小；当裂纹长度不变，铺层数增加时，固有频率增大。说明裂纹对固有频率的影响和复合材料层合板的固有属性有关，裂纹长度越长，复合材料层合板刚度越低，对固有频率影响越大。

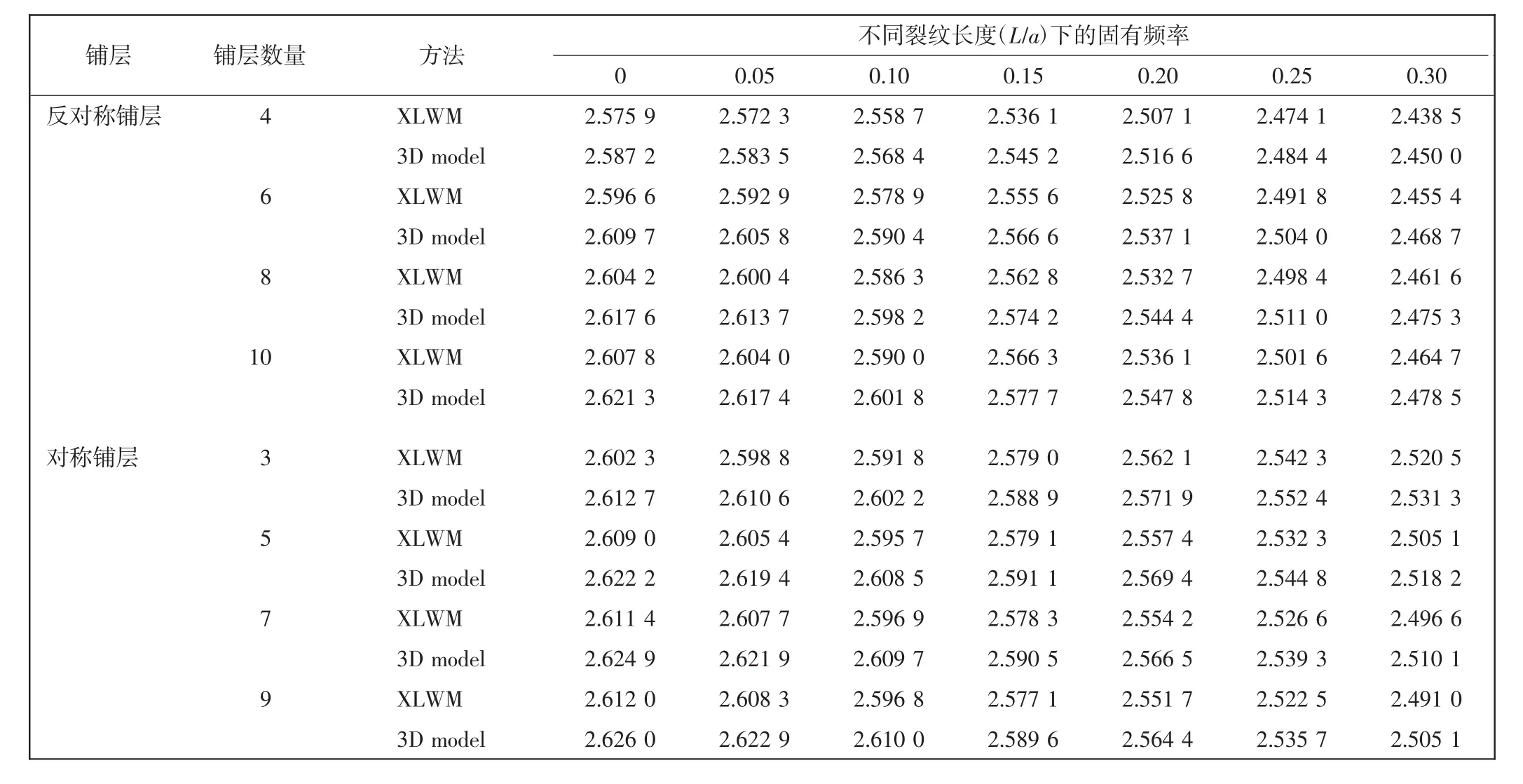
表3 不同方法下铺层数量及裂纹长度对固有频率的影响Tab.3 Influence of Layer number and crack length on fundamental frequency under difterent methods

由以上研究可知，在仅考虑减小裂纹对动态特性影响方面，应选择各向异性度小、分层多的复合材料层合板制作航空构件。在实际应用中，若受低速冲击影响，裂纹和分层等问题一起出现，这时裂纹表现出的影响更大，且裂纹长度会随着航空器的往复运行而增大，从而影响航空器的安全性，因此避免裂纹的产生并使用无损检测技术及时有效地检测裂纹才能保证航空器的安全性。