太阳能微型无人机气动效率计算方法

卢 翔，徐显超，曾琼芝

（中国民航大学航空工程学院，天津 300300）

微型无人机整机设计往往参照高雷诺数飞行器，对低雷诺数的影响考虑较少[1-2]。关于低雷诺数下翼型的气动特性也有不少学者进行了相关研究。Drela[3]描述了低雷诺数下边界层的工作情况，并研究不同参数对翼型气动的影响。Zuo等[4]从减小单位时间能耗角度对低雷诺数翼型进行单点优化。张亚锋等[5]以升阻比为目标对低雷诺数翼型进行单点优化。以上基本是从微观层面进行研究，只针对某一典型雷诺数进行单点分析。

太阳能供电及任务需求导致该飞行器需要在一个较大的速度范围下飞行，由于低雷诺数下飞行器阻力系数随速度变化较大，同时配平阻力带来的气动损失也变化较大，现有微观、单点的计算方法将不再适用。考虑飞行器的该特殊性，充分分析了阻力系数随雷诺数的变化及配平阻力随速度的变化，并通过FLUENT数值仿真及实际飞行实验进行双重验证。

1 低雷诺数的影响及计算

1.1 设计要求

根据市场调研、运输要求等因素确定参数的边界条件：①起飞重量≤4.5 kg；②翼展≤2.3 m；③机身长度≤1.15 m；④尾翼形式为V尾。

1.2 机翼气动特性计算

在航空航天领域，雷诺数Re＜1.0×106被视为低雷诺数[6]。由图1可以看出，在低雷诺数下各迎角都呈现出翼型升阻比随雷诺数变化较大，高雷诺数下变化较小的趋势。

微型无人机一般工作的雷诺数范围为1.8×105～3.5×105。由图2可知，在该范围内翼型的升力系数不会随雷诺数发生较大变化，而阻力系数变化较大。由此可知，对于低雷诺数飞行器，雷诺数是阻力系数强相关参数，在该范围内升力系数不随雷诺数而变化。通过对可能使用到的翼型及雷诺数进行统计、建模，最后拟合成特定的函数用以设计该飞行器。

图2 雷诺数对升力系数及阻力系数的影响Fig.2 Influence of Reynolds number on lift and drag coefficients

对飞行器巡航状态进行估算，在巡航状态可能的迎角范围为-3°～6°，对该范围的数据进行统计。为了便于计算分析，雷诺数可表示为

其中：k为系数，海拔高度为3 000 m时，k=53 676；l为平均气动弦长（m）；V为飞行速度（m/s）。

考察的翼型为 NACA 63A612、FX 63-110-1、FX 63-110，飞行器可能采用的翼型数据，如图3所示。

从图3中可看出，这3个翼型在升力系数、阻力系数、升阻比及力矩系数上都有较大差别。飞行器巡航升力系数为0.5～0.7，对比同升力系数下各翼型的参数，如表1所示。

由表1可知，各翼型在同等升力系数下阻力系数及升阻比相差不大。从图3可看出：NACA 63A612翼型最大升力系数较小，同时在大迎角下升力系数曲线突然降低，该翼型在大迎角时容易出现突然失速发生危险，不予采用；FX 63-110翼型低头力矩系数过大，平尾需要产生很大的负升力用以配平，造成配平阻力过大，特别是飞行速度提高后，容易造成配平阻力剧增导致升阻比快速下降。因此，最终选择FX 63-110-1，该翼型有合适的力矩系数、较大的升阻比及最大升力系数。

图3 翼型的气动特性Fig.3 Aerodynamic characteristics of airfoil

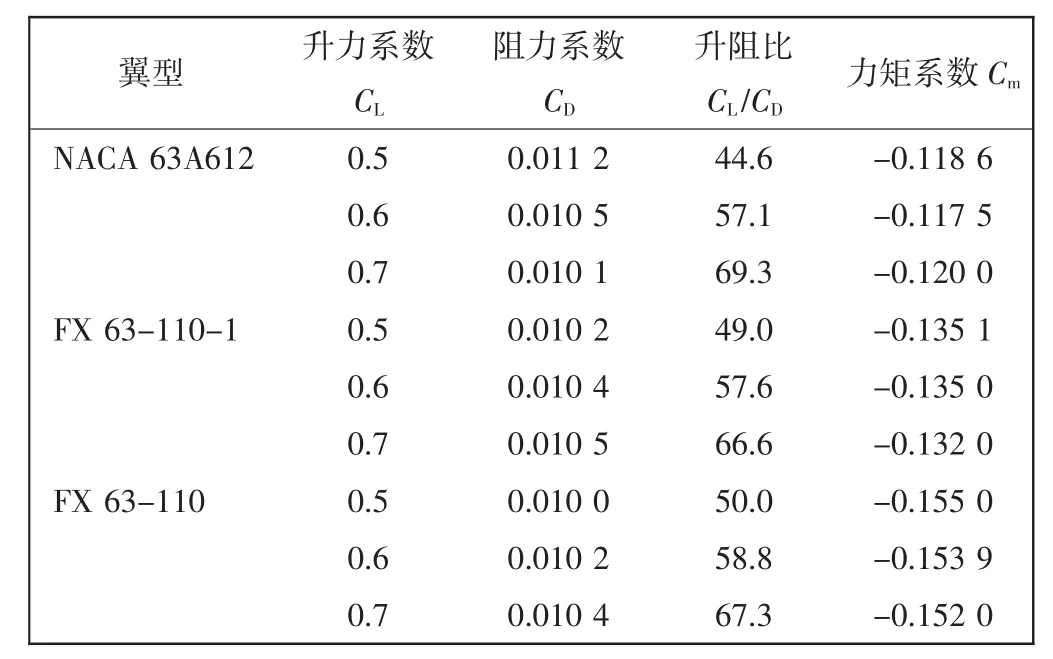
表1 各翼型参数对比Tab.1 Airfoil parameter comparison

对于同一架飞机，平均气动弦长为定值，雷诺数只与飞行速度相关，而飞行速度又将影响升力系数。假设同一飞行器速度分别为V1、V2，雷诺数分别为Re1、Re2，升力系数分别为 CL1、CL2，则有以下关系

由于暂时无法确定飞行器弦长及飞行时确切的升力系数，故根据现有数据可知巡航升力系数范围为0.5～0.7，推导得出其他雷诺数下的升力系数。通过翼型软件Profili计算不同翼型的雷诺数下的气动特性，如表2所示。

从表2中可知，当飞行器升力系数为0.5～0.7时，3种翼型阻力系数随雷诺数变化的趋势相近，并发现三次多项式曲线可很好地拟合曲线，如图4所示。

表2 雷诺数下的气动特性Tab.2 Aerodynamic characteristics under various Reynolds numbers

图4 阻力系数与雷诺数关系Fig.4 Drag coefficient vs.Reynolds number

为便于工程计算，以拟合的三次多项式作为雷诺数Re与翼型阻力系数Cdw间的函数关系进行计算，即

将式（3）转化为飞行速度V与翼型阻力系数Cdw的函数关系为

1.3 机身尾翼阻力计算

根据设计要求，该飞行器起飞质量为4.5 kg，考虑到运输要求，机身长度定为1.15 m。此外机身外形需要考虑能容纳有效载荷、动力系统、控制系统、电池等部件，外形为流线型以减小型阻。通过CATIA建模及曲面表面积分析，可计算得出机身浸润面积为0.40 m2。参考经验数据单位浸润面积系数Cfe=0.005 5，由机翼面积SW为0.5～0.7 m2可得出，以机翼为参考面积时机身阻力系数值为0.003 14～0.004 4，可记为0.002 2/SW，典型值为0.003 67。

由于采用全动V尾，尾容量可适当减小，尾翼浸润面积为0.12 m2，采用机翼面积作为参考面积，尾翼阻力系数为 0.000 94～0.001 32，可记为 0.000 66/SW，典型值为0.001 22。

1.4 整机气动性能

整机阻力系数为

其中：Cd0为零升阻力系数；Cdi为机翼诱导阻力系数；kbl为配平阻力对整机阻力的影响系数。

由《航空气动力工程计算手册》的数据可知，常规布局飞行器配平会造成一定的气动损失。当重心距离机翼前缘25%时，一般损失为6%；当重心距离机翼前缘40%时，一般损失为4%。根据以往经验，该飞行器重心位置距离机翼前缘33%左右，配平气动效率损失为 5%[7]，即 kbl=1.05。

该飞行器没有起落架等外置附属结构，零升阻力系数构成为

其中：kin为干扰阻力系数，一般取1.1；Cdw为机翼阻力系数；Cdf为机身阻力系数；Cde为尾翼阻力系数。

机翼诱导阻力系数为

其中：A为展弦比；e为机翼平面形状系数（奥斯瓦尔德效率因子的倒数），对于类椭圆的梯形机翼，e通常取0.9；CL为飞行器当前升力系数，即

其中：G为重力系数；F为升力，在巡航状态时，升力F等于重力；ρ为大气密度；V为飞行速度。

飞机的升阻比可表示为

该飞行器参数如表3所示，其中，SW，A为典型值。

表3 飞行器参数表Tab.3 Aircraft parameters

由于偏导数为多次函数，求解复杂，先做出偏导数图，结合二分法求解可得弦长l=0.25 m时：当V=16.5 m/s时，偏导数为0；V＜16.5 m/s时，偏导数小于0，函数递减；V＞16.5 m/s时，偏导数大于0，函数递增。因此，V=16.5 m/s时函数有极小值，对应的升阻比有极大值，求得极大值为18.38。

同理，可求得不同弦长时的情况如表4所示。随着弦长的缩短，展弦比变大，升阻比有一定的提高，但由于低雷诺数导致阻力系数增加，升阻比提高有限；平均气动弦长的改变并没有明显改变最大升阻比对应的速度，而是改变最大升阻比对应的升力系数；当平均气动弦长l为0.21 m及0.23 m时，升力系数较大，可能影响飞行安定性。

表4 平均气动弦长对气动参数的影响Tab.4 Influence of average aerodynamic chord length on aerodynamic parameters

同时，计算出不同飞行速度下零升阻力、诱导阻力及总阻力，如图5所示。由于阻力系数随飞行速度增加而减少，使得阻力增加幅度变小，总体变化与高雷诺数飞行器类似。

图5 阻力与速度的关系Fig.5 Drag vs.velocity

计算不同速度下升阻比及诱导阻力所占比例，如图6所示。在飞行速度16.5 m/s时升阻比达到最大值，在高雷诺数时不考虑机翼零升阻力变化，在诱导阻力等于零升阻力时，即诱导阻力等于整机阻力50%时升阻比最大；在低雷诺数时考虑机翼零升阻力变化，诱导阻力等于整机阻力45%时，飞行速度对应的升阻比最大。随着速度增大，两者诱导阻力所占比例趋于相同。由此可见低雷诺数与高雷诺数气动上存在一定差别。

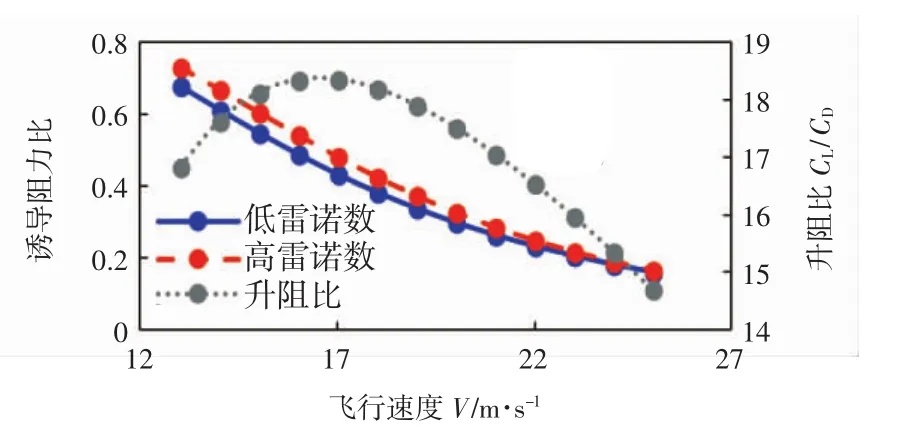
图6 诱导阻力比例及升阻比随速度变化关系Fig.6 Induced drag ratio and lifting drag ratio vs.velocity

代入弦长l计算不同飞行速度下的升阻比，如图7所示。随着速度偏离最佳速度，升阻比逐渐变小；对于该飞行器可行的设计范围内，弦长越短升阻比越高。为了便于铺设电池板及综合考虑其他因素，该飞行器平均气动弦长取0.25 m。

图7 升阻比与速度关系Fig.7 Fig.6 Lifting drag ratio vs.velocity

1.5 配平阻力计算

平尾需要产生向下的负升力进行配平，此时会产生一定的诱导阻力。同时，机翼需要产生额外的升力来平衡平尾的负升力，需增加升力系数，产生额外的诱导阻力。因此，考虑尾容量、整机焦点、配平阻力等因素进行计算。

整机焦点位置可表示为

其中：h0为机翼焦点位置，当与机翼弦长25%处连线后掠角为 0°时，h0=0.25；ηs为平尾效率，取经验值0.75；a1′为平尾修正升力线斜率；a2′为机翼修正升力线斜率；dε/dα为机翼迎角改变时平尾区域气流下洗角的变化率；vs为平尾尾容量，即

其中：SH为等效平尾面积；LH为尾力臂长度；SW为机翼面积；lW为机翼平均气动弦长。

机翼（平尾）升力线斜率要进行翼型升力线斜率的展弦比修正，即

根据经验，平尾展弦比A=4.5。为了便于研究，平尾选择常用翼型，其升力线斜率a1=0.1，且俯仰力矩系数稳定，代入式（12）求得a1′=0.071。由该飞行器气动参数可知，翼型升力线斜率a2=0.11/（°），该飞行器的展弦比 A=9.28，代入式（12）可得 a2′=0.091。

对于单翼飞行器有

将以上数据代入式（10）可得h关于尾翼面积的函数为

通常重心与整机焦点的距离为平均气动弦长的0.08，平均气动弦长为0.248 m，重心距离机翼焦点的距离可表示为

飞机维持平衡的条件为升力对重心的力矩T1、焦点力矩T2及平尾升力对重心产生的力矩T3之和为0。机翼升力对重心的力矩为

机翼焦点力矩为

平尾升力对重心产生的力矩系数为

尾翼升力为

式中，fe为正，方向向上。尾翼升力系数为

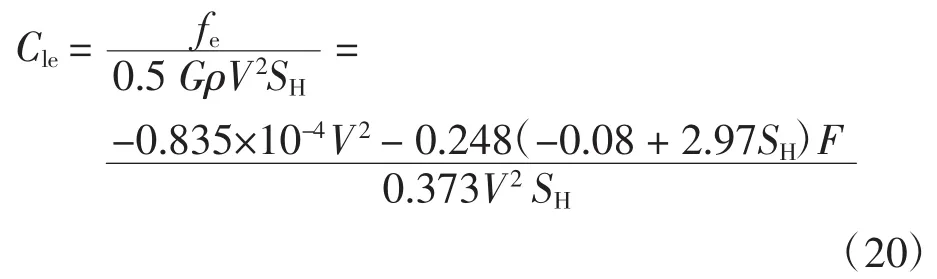
由尾翼升力系数、尾翼展弦比、平尾面积、飞行速度即可求解尾翼诱导阻力值fecdi。由于尾翼负升力造成机翼产生额外升力，升力系数提高并产生额外的诱导阻力，可表示为

可简化为

式中，W为起飞质量。

由图6可知该飞行速度下诱导阻力所占总阻力的比值Ncdi，总阻力为f，配平阻力增量为

根据以上公式，可求得配平阻力与平尾面积及飞行速度的关系，如图8所示。在该飞行器可能飞行的速度范围内，随着平尾面积增加，配平阻力与整机阻力的比值（阻力增加比）逐渐减小。当飞行器处于巡航速度16.7 m/s时：尾翼面积0.06 m2增加配平阻力比值为0.05，此时可求得尾容量为0.348；平尾面积0.07 m2增加配平阻力比值为0.036，此时可计算得尾容量为0.406。由于该飞行器采用全动尾翼，为避免操控过于灵敏，平尾面积取0.06 m2。

图8 平尾面积与配平阻力比例关系Fig.8 Tail area vs.trim resistance

通过式（23）可计算得出配平阻力fH，从而可计算该飞行器在可能飞行的速度范围内配平阻力所占比例，如图9所示，随着飞行速度增加，配平阻力占整机阻力比例逐渐增加。

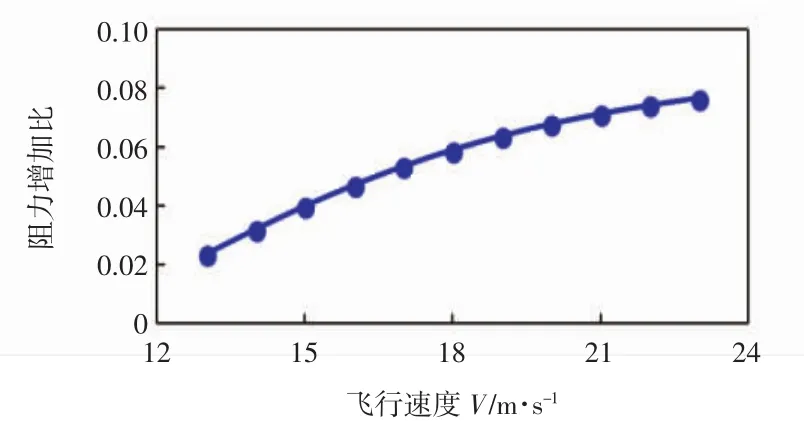
图9 速度与配平阻力比例关系Fig.9 Speed vs.trim resistance

在计算飞行器气动参数时，所有飞行速度都以配平阻力相对总阻力增加量为5%进行计算，根据以上数据对气动参数进行修正，结果如表5所示。

表5 升阻比随速度变化关系Tab.5 Lifting drag ratio vs.velocity

2 FLUENT数值仿真及飞行实验

FLUENT数值仿真采用低雷诺数k-ε模型，构建迎角为-2°、0°、2°、4°、6°、8°、10°的网格文件分别进行计算。网格数量为180万左右，非结构网格，网格歪斜比小于0.8。图10为压力场云图，表6为仿真所得的数据。

图10 低雷诺数k-ε模型压力场云图Fig.10 Pressure field nephogram of low Reynolds number k-ε model

表6 低雷诺数k-ε模型气动参数Tab.6 Aerodynamic parameter of low Reynolds number k-ε model

飞行测试采用自研专用飞行测试仪器，可实时采集飞行器飞行速度、输入功率、拉力、发动机扭矩、发动机转速等物理量。当飞行器以匀速直线飞行时，拉力等于阻力，重力等于飞行器升力。重力为已知量，所以只需拉力和飞行速度数据即可得出升阻比与飞行速度的关系。图11显示飞行中的飞行器及测试设备，图12为实际测试飞行，图13为计算、仿真及实验结果的对比。

图11 飞行器以及测试设备Fig.11 Aircraft and test equipment

从图13可知，计算值、仿真值及实际值在多数情况下（飞行速度14～23 m/s）是接近的。在速度低至14 m/s时突然产生巨大偏差，是因为此时飞行器处于失速状态或临近失速状态，而该算法用于计算巡航状态的气动效率，无法计算失速时的情况。由于测试要求飞行器处于匀速巡航状态，失速后无法测试数据，且为了确保飞行安全，实际飞行测试速度不得低于14 m/s。该计算方法相对于FLUENT仿真数据与实际值更加吻合；计算值略高于实际值，且随着速度增大，计算值与实际值的偏差也在变大，其原因可能是干扰阻力系数取值过小所致。

图12 实际测试飞行Fig.12 Test flight

图13 实验结果对比Fig.13 Result comparison

3 结语

通过建立低雷诺数下翼型阻力与雷诺数关系及对配平阻力进行建模，修正了配平阻力，从而建立了针对太阳能-锂电池混合动力微型无人机的气动效率计算方法。通过对比实际飞行数据及FLUENT数据可知：在大部分飞行速度下，该计算方法能与实际及仿真结果吻合；当速度过低，飞行器处于失速或邻近失速时，该计算方法会产生很大偏差。因此该计算方法适用于计算巡航速度及低雷诺数下的气动效率，但不适用于计算失速或邻近失速状态下的气动效率。