压力容器中锥壳-圆柱壳连接结构的分析设计方法(二)

(1.清华大学 工程力学系,北京 100084；2.中国石化工程建设公司,北京 100101)

0 引言

在我国压力容器现行标准[1-2]中，锥壳小端采用的设计准则式为：

Pm⟹SⅠ≤Sm

(1)

PL⟹SⅡ≤1.1Sm

(2)

PL+Q⟹SⅣ≤3.0Sm

(3)

众多的算例都显示，在锥壳小端与圆柱壳连接部位，控制补强设计厚度的准则是SⅡ的许用值，需要对此类结构SⅡ许用值的合理取值进行研究。本文通过塑性分析建议：以下列准则式代替准则式(2)，即：

ps/p≥1.5

(4)

式中ps——结构的塑性极限压力；

p——设计压力。

由文献[5]所给出的弹性薄壳理论解，计算得到最大总体加局部薄膜应力强度SⅡ。将设计准则式(2)由准则式(4)替换，依据薄壳理论解所得弹性名义应力的SⅡ，再通过弹塑性分析，由结构的极限压力准则式(4)确定SⅡ的许用值，从而确定结构所需的补强系数Qs。

1 内压作用下锥壳大、小端分别与圆柱壳相连接结构的塑性极限压力

20世纪后期，文献[6]对锥壳大、小端分别连接圆柱壳的结构导出了塑性极限分析的理论解，其力学模型见图1[6]。

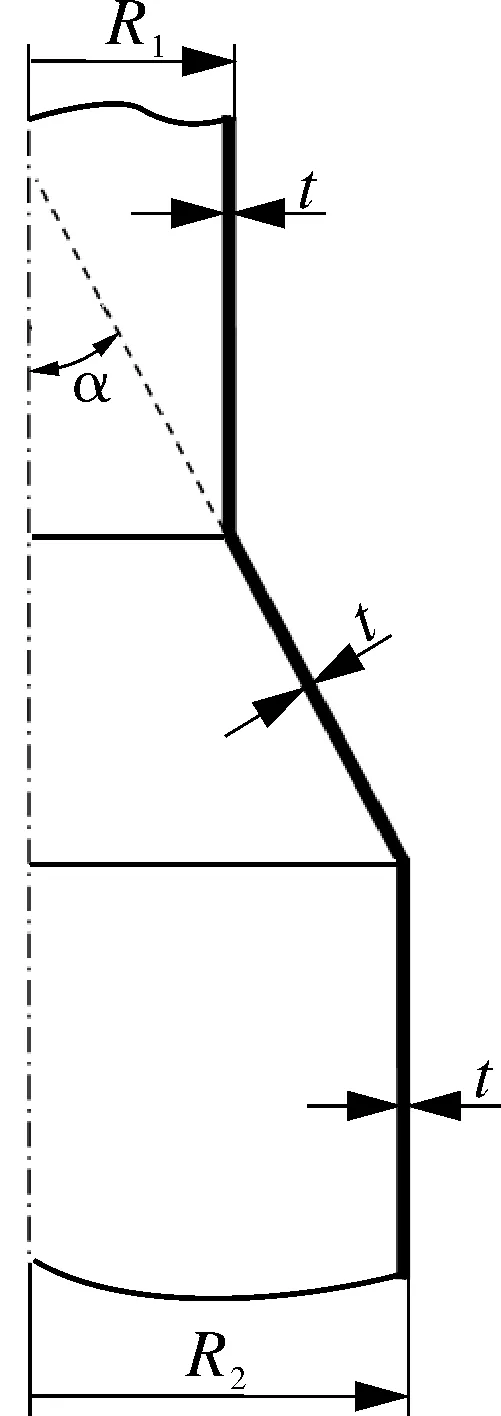
t-壳体的厚度δr;α-锥半顶角;R2,R1-大、小端圆柱壳半径

图2 5种可能的塑性流动机构

文献[6]中对圆柱壳采用单矩弱作用的Tresca屈服条件，对锥壳采用双矩弱作用的Tresca屈服条件[7]，得到了极限分析的完全解;文献[6]中还给出不同几何参数(α,R2/R1,t/R1)条件下结构可能发生的5种塑性流动机构(见图2[6])及塑性流动机构与这些几何参数的关系，图3[6]示出其中的一例。其中塑性流动机构A为锥壳大端与大圆柱壳先破坏，发生在α和R2/R1较大、t/R1较小时；塑性流动机构C,D为锥壳小端与小圆柱壳先破坏，塑性流动机构E为小圆柱壳先破坏，这三种塑性流动机构发生在α和R2/R1较小时；塑性流动机构B为锥壳大、小端和大、小圆柱壳同时破坏，发生在几何参数为中间状态时。文献[6]还给出了每组参数(α,R2/R1,t/R1)对应的无量纲塑性极限压力psR1/(σst)(其中，σs为材料的屈服应力)。受当时研究条件所限，该项工作未能进一步验证和应用。

图3 锥壳变径段塑性流动机构与几何参数的关系

文献[8]中通过理想弹塑性小变形有限单元法对文献[6]进行了验证，证明了文献[6]根据塑性理论完全解所给出各种参数下的结构塑性流动机构与极限压力的可靠性。表1列出文献[8]所给部分算例的几何参数，这些算例对应的流动机构见图3[6]。

表1 各算例的锥壳几何参数与对应的塑性流动机构

图4示出文献[6]理论解和文献[8]所给算例有限元解的比较，图中线形数据为文献[6]所给理论解；离散点为对应算例用弹塑性有限元法得到的极限压力。由弹塑性变形历史曲线，分别用JB 4732—1995[2]附录B.5规定的“两倍弹性线斜率法”和ASME—2017[4]5.2.4节规定的“结构整体失稳法”两种不同的定义方法给出了塑性极限压力，如图5所示，在图4，5中给予不同的标志。图4显示理论解[6]与有限元解[8]能够较好地吻合，证明了文献[6]塑性理论完全解的可靠性。其中，“两倍弹性线斜率法”较“结构整体失稳法”更为保守，在多数情况下，理论解与按“结构整体失稳法”得到的塑性极限压力数值解一致，但当结构的锥半顶角和和厚径比均较大(如算例a4，a5,a6等)时，“结构整体失稳法”所得到的极限压力数值解高于理论解。

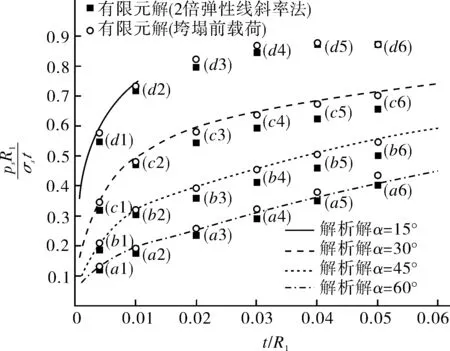
图4 极限分析理论解与弹塑性有限元解

图5 算例a2极限压力的确定

关于各种参数情况的塑性极限分析还说明，若结构参数(α较小)显示：先发生D,E两种锥壳和小端圆柱壳先破坏的塑性流动机构时，由于此参数下锥壳大端与圆柱壳连接处弯曲应力较小，一次局部薄膜应力强度大，所以控制锥壳变径段设计厚度的准则必定为设计准则式(4)；若结构参数(α较大)显示：先发生A类大端圆柱壳塑性流动机构时，控制锥壳变径段设计厚度的准则可能为设计准则式(4)，由于此参数下锥壳大端与圆柱壳连接处有较大的弯曲应力，一次加二次应力强度较大，所以还需进行结构安定性校核，控制设计厚度的准则也可能为设计准则式(3)。

2 内压作用下与圆柱壳相连的锥壳小端补强设计方法

弹性分析已经表明，控制小端设计厚度的准则是其一次薄膜应力强度SⅡ。鉴于前言中所述，目前如何确定一次局部薄膜应力强度的许用值尚存在问题，下面通过分析给出了安全可靠的工程设计方法：选取不同结构参数α,t/R1,R2/R1对应的结构，计算其塑性极限压力ps，将ps/1.5作为设计压力p，用弹性薄壳理论精确解对同一结构进行计算，发现小端处计算得到的SⅡ/Sm值既不等于1.1，也不等于1.5；在大多数情况下，许用值取1.5Sm安全裕度不够，而许用值取1.1Sm又过于保守。本文采用如下方法得到锥壳变径段的补强设计方法：

(1)针对不同的结构参数(α,R2/R1)，在给定p/Sm值(Sm=σs/1.5)下设定t值，应用文献[5]中的弹性薄壳理论解计算SⅠ,SⅡ和SⅣ；

(2)改变t值，重复弹性应力分析，直至满足现行标准[1-2]原有准则式(1)～(3)；

(3)通过进行塑性极限分析结果迭代调整t值，使调整后的t值在给定p/Sm,α,R2/R1值和该t/R1值下得到的塑性极限压力对于设计压力的安全系数ps/p≥1.5(且接近1.5)；

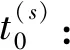
(5)

式中Di——小端圆柱壳内直径。

计算与圆柱壳相连接的锥壳小端补强系数Qs：

(6)

根据上述方法所得到的锥壳小端补强系数Qs曲线见图6。

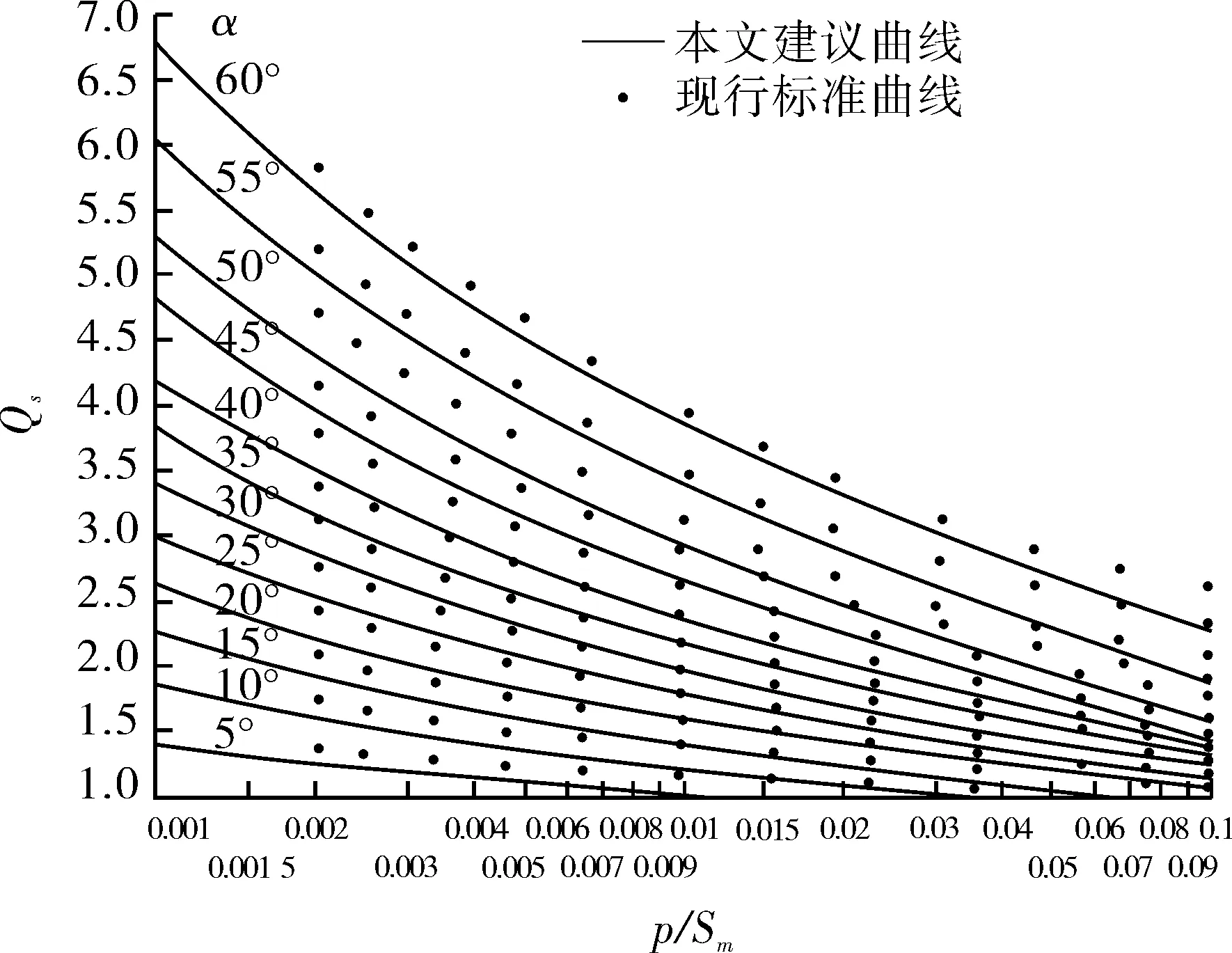
图6 锥壳小端分析设计方法加强系数Qs曲线与

表2 按本文锥壳小端设计曲线设计结构的塑性极限压力对于设计压力的安全系数

注：表中除注明者外，其余算例均为R2/R1=1.2，其中kL为该算例对应的一次局部薄膜应力强度的许用值SⅡ/Sm

图6还示出了与原标准[1-2]中曲线的对比结果，其中实线为本文所给出，点为标准[1-2]中所给Qs值(按设计准则式(1)～(3))。按图6中Qs值所设计的锥壳变径段小端，用弹塑性小变形有限元法计算塑性变形历史并绘制曲线，按照“两倍弹性线斜率法”给出对应的塑性极限压力，按设计准则式(4)控制设计厚度的典型算例结果见表2。

(1)本文的分析和图6与表2显示，原标准[1-2]所采用的设计准则式(2)略为保守：所有算例对一次局部薄膜应力强度SⅡ的许用值超过1.1Sm，都可以得到ps/p略大于1.5的结果；本文建议曲线具有合理的安全裕度，锥壳变径段小端加强系数比原标准[1-2]所给补强系数值略小。

(2)综合图6和文献[5]关于锥壳大端与圆柱壳连接的分析可知，对于R2/R1较大的长锥壳变径段(如R2/R1=1.5)，当p/Sm>0.03以及α>35°时，由于锥顶角和设计压力较大时，锥壳大端的总体一次薄膜应力加大，锥壳大端设计厚度都由准则式(1)控制(见文献[5]中图10)，而图6显示锥壳小端的加强系数Qs值随p/Sm值的增大而减小，锥壳变径段的设计厚度是按设计准则式(1)控制的。

3 大、小端分别与圆柱壳相连的锥壳变径段两端边缘效应耦合时的设计准则讨论

文献[5]已指出，与不考虑边缘效应耦合所得简单边界效应解的传统概念相反，锥壳变径段两端边缘效应的耦合作用使锥壳中的一次局部薄膜应力降低，同时采用设计准则式(1),(3),(4)来替代原有的设计准则式(1),(2),(3)，给出了考虑边缘效应耦合作用的锥壳变径段补强系数Qs的设计曲线。本文进一步论证该设计方法的安全性以及对于此类复杂结构，采用塑性极限准则的必要性。

表3列出文献[5]所提出的考虑边缘效应耦合作用的短锥壳变径段设计方法所对应典型算例的极限压力，并同时给出这些算例对应的kL=SⅡ/Sm值。

表3 锥壳变径段两端边缘效应耦合结构的塑性极限压力与设计压力之比及塑性流动机构类型

(1)表3显示,考虑锥壳变径段两端边缘效应的耦合作用所给出的设计方法有足够的安全裕度，所有算例的结构塑性极限压力对于设计压力的安全系数ps/p都大于1.5。

(2)表3显示,锥壳变径段两端边缘效应的耦合作用使锥壳与圆柱壳连接处的一次局部薄膜应力进一步降低，部分满足塑性极限强度设计准则式(4)的算例，该处kL=SⅡ/Sm值甚至小于1，远小于按弹性分析设计准则式(2)的要求。图7,8分别示出算例No.1(α=60°,R1=1 000 mm,R2/R1=1.1,t/R1=Qsp/Sm=0.006 25,p=0.2 MPa)按照薄壳理论解和有限元数值解所得锥壳变径段中环向薄膜弹性名义应力分量和经向薄膜加弯曲弹性名义应力分量的对比结果，表明薄壳理论的精确解是可靠的，而对于短锥壳变径段，简单边界效应解与有限元、精确解的误差太大，如一次薄膜应力分量远大于有限元和精确解的结果。

(3)从表3可以看出，对于这些锥壳变径段非常短、两端壳体边缘效应互相耦合的结构，其塑性流动机构大多属于图2中的塑性流动机构B，即锥壳两端与大、小圆柱壳连接处及大、小圆柱壳中均出现塑性铰，3个元件同时发生塑性流动的情况。

图7 算例No.1经向薄膜加弯曲弹性名义应力

图8 算例No.1环向薄膜弹性名义应力分量

表3中各算例是以塑性极限准则式(4)控制设计厚度的，本文将进一步分析对于此类复杂结构，不宜采用弹性名义应力准则式(1)～(3)。以图7,8，即表3中算例No.1为例，该算例的基本参数为：α=60°,R1=1 000 mm,R2=1 100 mm,p=0.2 MPa，材料屈服极限σs=300 MPa,若取t=6.25 mm，由t/R1=0.006 25，计算其弹性名义应力强度：km=SⅠ/Sm=0.352<1,kL=SⅡ/Sm=0.75<1.1,kP+Q=SⅣ/Sm=2.3<3。也就是说，按照弹性分析及相应的设计准则，该算例可承受比0.2 MPa更高的设计压力，但是进一步的塑性分析表明，对于此类短锥壳变径段，应用传统的与弹性名义应力分析方法相应的设计准则不能给出可靠的设计结果。

算例No.1由有限元法计算得到的弹塑性变形历史曲线及按照文献[2]与文献[4]两种不同定义的塑性极限压力ps下的结构应力分布云图见图9。图7显示在算例No.1的锥壳大端P2截面、小端P1截面分别具有负最大和正最大的弯矩，当结构承受设计压力p=0.2 MPa时，P2和P1截面附近锥壳和大、小端圆柱壳中的弹性名义应力已经远超过材料的屈服极限。该两处壳体表面的应力已经达到屈服极限，不能再增加，但是从弹塑性分析(见图9)可知：p=0.2 MPa时，该两处沿旋转壳体周圈横截面中部仍为弹性，整个变径段壳体结构并没有发生塑性流动；其后，随着压力的增大，旋转壳弹性部分应力将沿着该两处锥壳和大、小端圆柱壳的全截面及其经向逐渐增大，直至大部分锥壳和与锥壳连接处的部分圆柱壳都进入塑性极限，形成几何可变的塑性流动机构，发生流动。对于理想弹塑性有限元分析得到的结果，按两倍弹性线斜率定义[2]，ps=0.304 MPa；若按文献[4]中的定义，理想弹塑性有限元程序可计算出的小端处平行圆最大径向位移为15.8 mm，对应的极限压力为0.34 MPa。

图9 算例No.1弹塑性变形历史曲线和应力分布云图

若按照传统弹性名义应力的设计准则，当SⅣ/Sm=3时，该算例可以承受比0.2 MPa更高的设计压力(0.261 MPa)。但是，按照弹塑性有限元分析，当材料的屈服极限σs=300 MPa=1.5Sm时，它仅可承受ps=0.304 MPa的极限压力(按两倍弹性线斜率定义[2])，安全裕量仅为1.165。即使按照最大塑性变形时所对应的ps=0.34 MPa计算，安全系数也只有1.3。

由于该算例的锥壳非常短，这种沿壳体经向应力增加达到屈服极限的过程容易完成，所以用传统的弹性名义应力设计准则将造成很大误差、且安全裕度不够。

文献[6]的理论解给出了当R2/R1=1.1时结构在极限压力下塑性流动机构与结构参数的关系，见图10[6]。可以看出，算例No.1的破坏模式为图2中的塑性流动机构B。图11[6]示出锥壳中弯矩(Ms,Mθ)、薄膜内力素(Ts,Tθ)的双矩弱作用Tresca屈服条件，当锥壳中内力素位于屈服面内，即属于弹性范围，增大到屈服面上即进入塑性，根据理想塑性材料的假设，锥壳中的内力素不可超出屈服面。发生塑性流动机构B时，锥壳中的弯矩Ms和Mθ、薄膜内力素Ts和Tθ对应于图11中的加粗线条，它们都位于屈服面上。

图10 R2/R1=1.1时锥壳变径段的塑性流动机构

图11 锥壳的双矩弱作用Tresca屈服条件

按照文献[6]的理论解，在该参数下算例No.1的无量纲极限压力为psR1/σst=0.17,ps≈0.318 MPa，理论解与有限元解分析得到的结构塑性流动模式一致，理论解所得塑性极限压力介于由弹塑性有限元法按两种不同定义方法所得的塑性极限压力之间，故文献[2]中所规定的两倍弹性线斜率定义方法所得极限压力偏于保守。

4 锥壳两端边缘效应耦合时短锥壳变径段的设计方法

根据锥壳与大、小端两个圆柱壳相连接的力学模型，由弹性薄壳理论的精确解和塑性极限压力和安定性准则式(1),(3),(4)，本课题组进一步得到了短锥壳变径段的分析设计方法。大量算例分析发现：

(1)当α<45°时，短锥壳两端的边缘效应耦合作用较小，对于其设计厚度的影响可以忽略；

(2)当α≥45°时，与现有标准[1-2]相比，考虑变径段短锥壳两端的边缘效应耦合作用，使加强段设计厚度有所减薄；

(3)α,t/R1越大，此种耦合作用越大；

(4)在α≤60°的范围内，当DiL/Dis>1.35时，不需考虑边缘效应的耦合作用。

图12示出了两例短锥壳变径段加强系数设计曲线。当p/Sm较大时，图中未给出Qs的部分为变径段过短，已不属于薄壳的结构。

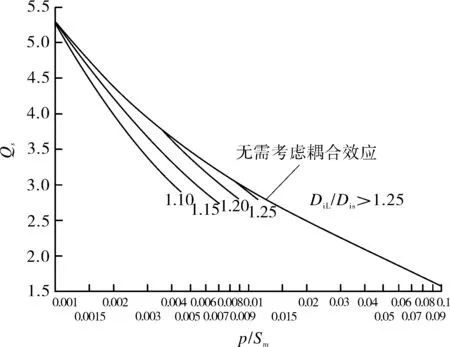
(a)α=50° (b)α=60°

图12 考虑锥壳变径段大、小端边缘效应耦合作用时的Qs值

5 结语

本文基于塑性极限分析理论与理想弹塑性有限元，对锥壳大、小端分别与圆柱壳相连接的结构进行了极限压力分析，提出采用结构极限压力ps与结构设计压力p的比值ps/p≥1.5替换传统的弹性名义应力设计准则SⅡ/Sm=1.1(或1.5)。根据所提出的设计准则，对锥壳小端与圆柱壳连接的结构以及短锥壳变径段分别与大、小端圆柱壳连接的结构提出了加强段的设计方法。弹塑性分析结果证明所提出的方法和设计准则安全合理。