地基不均匀沉降和风载荷联合作用下的大型储罐屈曲分析

2019-05-13

压力容器 2019年3期

(浙江大学化工机械研究所，杭州 310027)

0 引言

现役的储油罐大部分建在沿江、沿海地区的湿陷性土壤上，由于土层构造复杂，储罐地基很容易产生沉降与变形[1-3]；同时在夏季，这些地区容易遭遇台风等突发性气候，大型储罐是一种典型的空间圆柱薄壳结构，径厚比大，刚度小，在暴风甚至长时间弱风的作用下会发生屈曲失效[4-6]。

在役储罐的检验与安全评价是目前的研究热点。雷翔[7]以几种不同尺寸的大型变壁厚储罐为对象，研究其在实测不均匀沉降作用下的结构响应，发现储罐仅在沉降作用下就有可能发生屈曲失稳；如果储罐在沉降下未发生屈曲变形，则可以视其为储罐的结构缺陷。Jiao等[8]通过多点扰动法研究发现,初始几何缺陷的存在会使薄壁圆柱壳的力学稳定性降低。Portela等[9]采用有限元方法，分析了拱顶储罐的风致屈曲机理和储罐的结构响应，并讨论了储罐缺陷对储罐稳定性能的影响。Chen等[10]在综合考虑几何非线性和大变形基础上，模拟分析了由沉降引起变形的储罐在轴压作用下的屈曲行为，发现沉降导致的储罐局部压应力可削弱储罐轴压稳定性。王昕等[11]以某热质储罐为对象，研究了储罐在自重、内压、风载荷、雪载荷等多种组合载荷工况下的强度破坏问题，发现多种载荷同时作用于储罐比单一载荷作用时危害更大。但现有针对储罐屈曲的研究还多局限于单一载荷作用，对于地基不均匀沉降和风载荷联合作用下的屈曲行为研究还鲜有涉及。

本文基于实测沉降数据，对在役储罐抗风稳定性进行分析，建立两者联合作用下储罐屈曲的数值模拟分析方法。

1 屈曲分析方法

本节从储罐模型简化、不均匀沉降处理、风载荷模型等方面，介绍储罐屈曲数值分析模型的建立方法。

1.1 模型简化

固定顶储罐结构如图1所示，主要包括罐壁、罐顶、罐底板及接管等附属结构。为了节约成本，罐壁通常采用变壁厚结构。相比于罐壁，不均匀沉降和风载荷对罐顶和罐底板的影响很小，可以通过设置边界条件来进行替代[12]。据此，对储罐结构模型进行如下简化与约定：

(1)风载荷作用下，储罐的空罐状态更为危险，故以空罐状态为研究对象；

(2)通过约束罐壁顶部的径向位移来等效储罐罐顶的影响；

(3)罐底板对罐壁的作用通过约束罐壁底部的径向位移和周向位移来代替；

(4)忽略接管等附属结构对罐壁的影响。

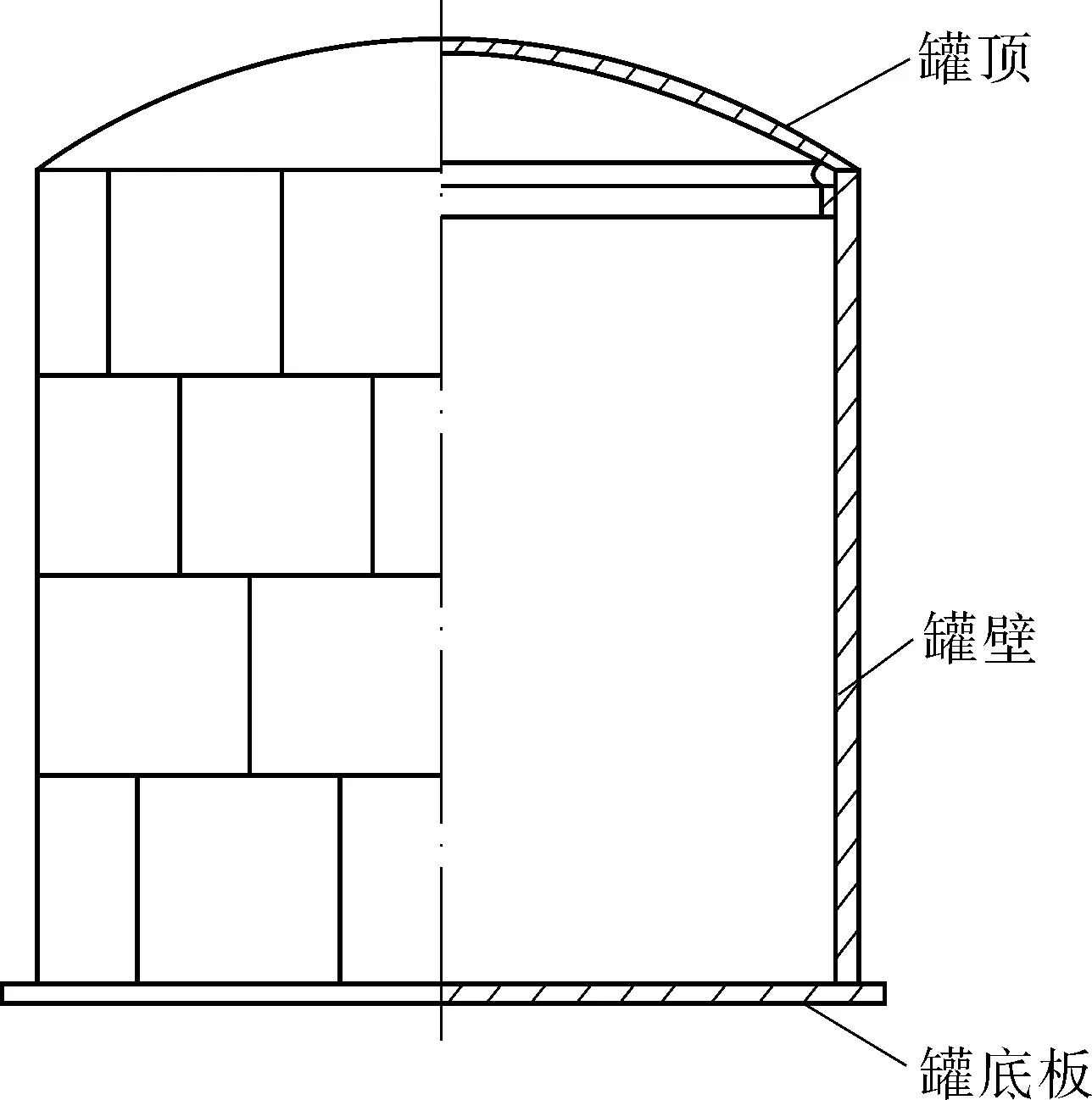
图1 固定顶储罐结构示意

1.2 不均匀沉降处理

罐壁底部的沉降可以分为整体均匀沉降、整体倾斜沉降和不均匀沉降。其中不均匀沉降对于储罐结构的影响通常是最大的，本文重点讨论不均匀沉降对储罐屈曲行为的影响。

基础沉降量是通过设置在储罐罐壁底部的沉降观测点测量得到的，但实测沉降值仅能代表该测量位置的沉降量。要想真实反映储罐沿罐周方向的沉降情况，需要基于离散的实测沉降数据拟合出连续的沉降曲线。本文采用文献[13]中提出的沉降曲线拟合方法，得到连续的罐周沉降曲线。

当沉降观测点数为偶数时，沿罐壁底部周向连续分布的沉降值表达式为[13]：

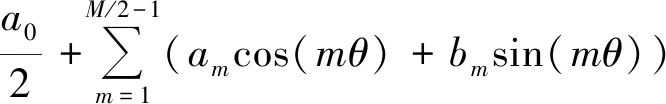
(1)

式中S——实测沉降值，mm;

m——傅里叶阶数;

a0,am,bm——待定系数;

M——沉降观测点个数;

θ——周向角度,(°)。

式(1)中，待定系数am，bm的表达式为：

(2)

当观测点数为奇数时，沿罐壁底部周向连续分布的沉降值表达式为：

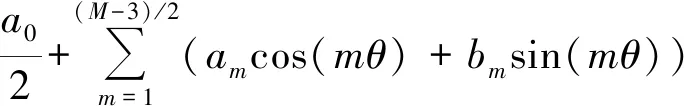
(3)

式(3)中待定系数am,bm的表达式与式(2)类似，在应用时仅需对am,bm中的傅里叶阶数m取值范围进行调整,即：计算am时，m=0,1,2，…，(M-1)/2；计算bm时，m=1,2，…，(M-1)/2。

式(1)和式(3)中m≥2的项，代表不均匀沉降，记为U(θ)，将其施加于罐壁底部，作为轴向边界位移条件。

1.3 风载荷模型

风载荷是由于空气流动对结构产生的载荷，其数值与风速的平方成正比。风载荷沿储罐的高度和周向的分布都是变化的，但沿高度方向上变化并不明显。为保守起见，通常取罐顶风压值为风压幅值，忽略风载荷沿高度方向上的变化[14]。

表1 风载荷分布函数中傅里叶系数

根据GB 50009—2012《建筑结构荷载规范》规定，风压幅值的计算公式如下：

(4)

式中λ——风压幅值，Pa;

μs——风载荷体型系数;

μz——风压高度变化系数;

βz——高度z处的风振系数;

ω0——基本风压，Pa;

“屌丝”，原为粗语，现今已成为青年群体中的流行语和文化现象。从对“李毅吧”粉丝的称呼到现在流行的“屌丝”涵义已经大相径庭。“屌丝”已不是原来特指的那一群出身卑微、内心充满纠结、无奈面对现实的年轻男性，而有着丰富的内涵。有的青年以自嘲的方式自称“屌丝”，将自己与“高富帅”、“白富美”作区分；有的则用来贬责他人；有的以玩笑用之……“屌丝”已变成当下在网络上、在青年群体中流行的一种时尚、一种独特的文化现象。

v0——基本风速，m/s。

风载荷沿周向不同角度分布差别较大。Rish等[15-16]通过实测、数值模拟等方法，总结得到风载荷沿圆柱壳的分布函数如下：

(5)

式中p——风载荷，Pa;

i——阶数;

ki——傅里叶系数，列于表1。

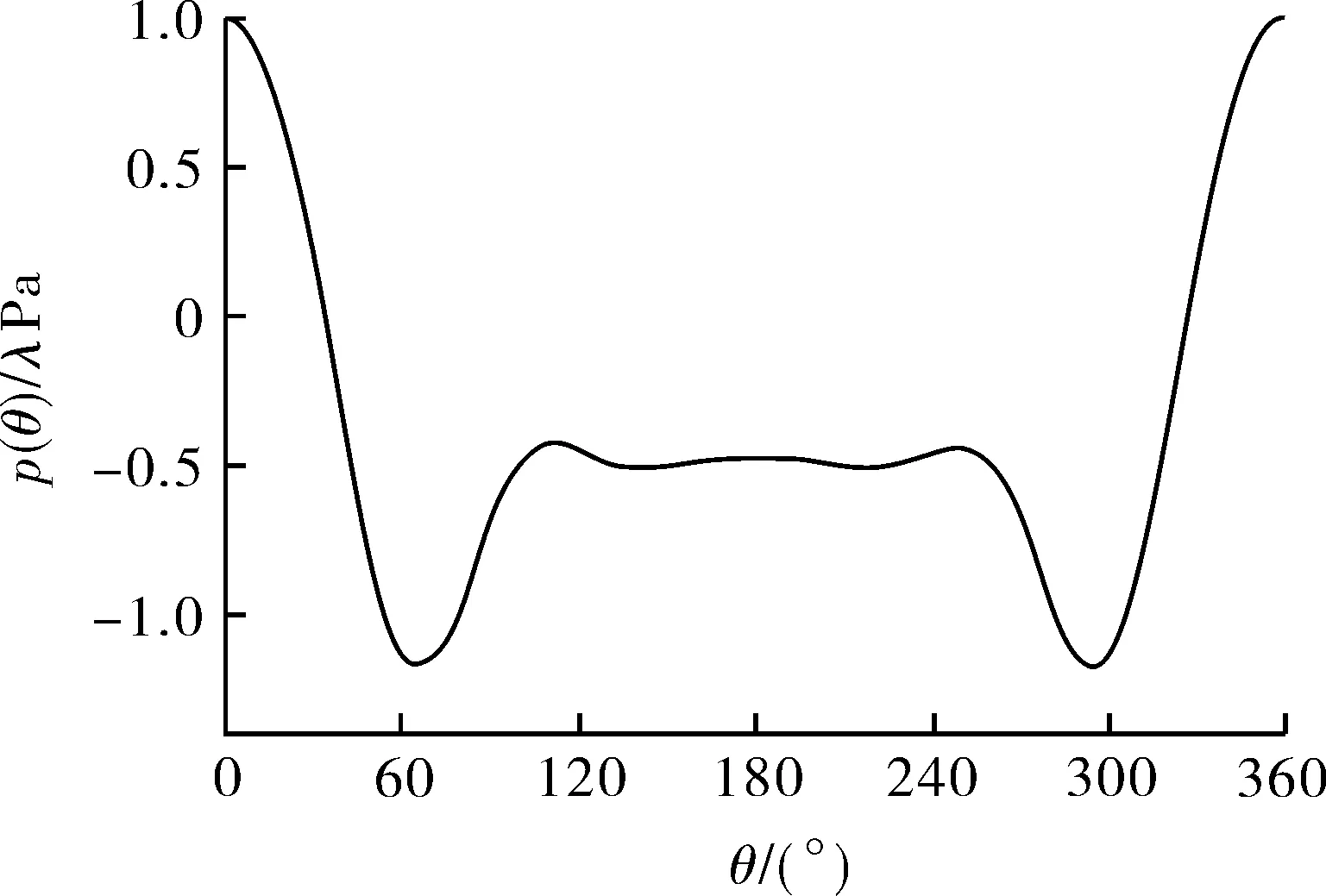
图2 罐周风载荷分布规律曲线

(a)α=0° (b)α=90°

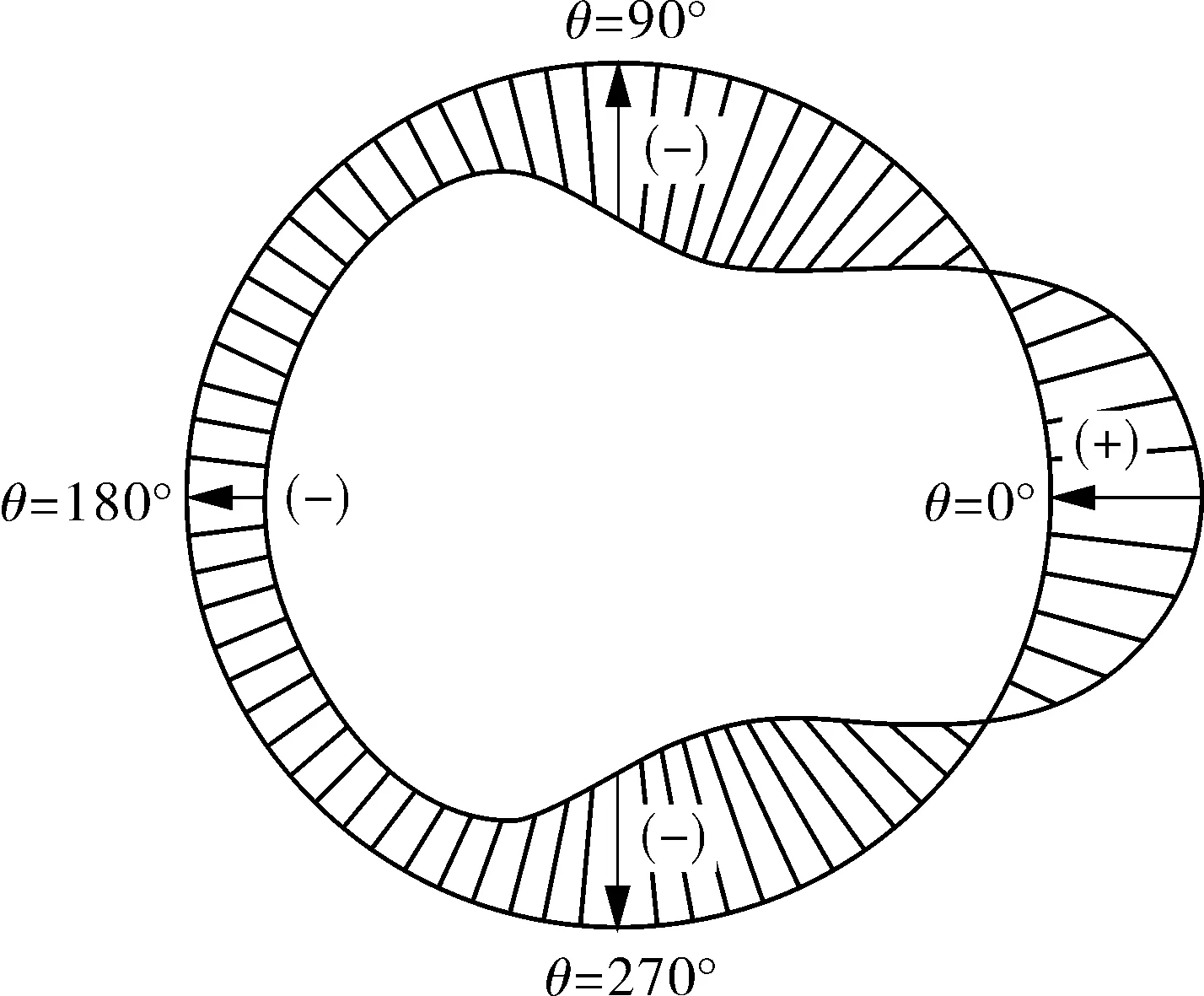
图3 罐周风载荷分布示意

由表1中的傅里叶系数，可以得到储罐的周向风载荷分布规律曲线，如图2所示;据此绘制风载荷沿罐周分布示意图，并约定了储罐周向角度θ=0°的位置，如图3所示。风载荷最大正向压力作用于储罐的周向角度定义为风载荷的风向角，记为α。图3(a)中，α=0°的风载荷作用于罐壁，θ在±30°范围内，为储罐的迎风受压区，储罐受到向内的正向压力，正向压力在θ=0°处最大；在其余范围内，储罐受到沿壁面向外的负向压力，并且在大约θ=±65°位置处负向压力达到最大，数值约为最大正向压力的1.2倍。

1.4 两者联合作用的屈曲数值模拟方法

地基的不均匀沉降随储罐服役时间不断变化，是长期存在于储罐底部的轴向位移边界条件。本文研究不均匀沉降对储罐抗风性能的影响，故先将不均匀沉降施加于罐壁底部，待加载完全后，再于罐壁上施加风载荷边界条件。

基于非线性大变形理论，使用Riks弧长法开展地基不均匀沉降和风载荷联合作用下储罐的屈曲模拟，可以获得储罐在风载荷作用下的全过程响应，同时可得到储罐发生屈曲时对应的临界风载荷比例系数LPFwc。通过换算，即可获得使储罐在不均匀沉降下发生风致屈曲的临界风载荷，如LPFwc=0.8，即为风载荷达到0.8p(θ)时，储罐在风载荷作用下发生了屈曲。

由于沉降分布的不均匀性，风载荷以不同的风向角作用于储罐，会导致结构产生不同的响应。在数值模拟时，通过改变风载荷的风向角α，开展这一问题的研究。

2 工程案例分析

本节先分析不均匀沉降和风载荷单独作用时储罐的屈曲响应，再将联合作用下的结构响应与其对比，并分析不均匀沉降分布形式对储罐抗风性能的影响。

2.1 固定顶储罐有限元模型建立

以浙江省舟山地区某20 000 m3固定顶储油罐空罐状态为例，基于ABAQUS软件建立有限元模型。储罐内径∅42 000 mm，罐壁总高17 000 mm，罐壁层数n=10，每层罐壁高度记为h，壁厚记为δ，罐壁材料Q345R，弹性模量E=2.06×105MPa，泊松比υ=0.3。储罐罐壁的几何参数如表2所示。

表2 储罐罐壁几何参数

注：罐壁层数n自下向上计数

储罐几何模型如图4所示。ABAQUS中的4节点四边形有限薄膜应变线性减缩积分壳单元S4R性能稳定，适用范围很广，可以较好地模拟薄壳结构的变形响应[2]。故采用S4R单元进行网格划分，网格单元数156 200，节点数157 300。经验证，可满足网格无关性要求。

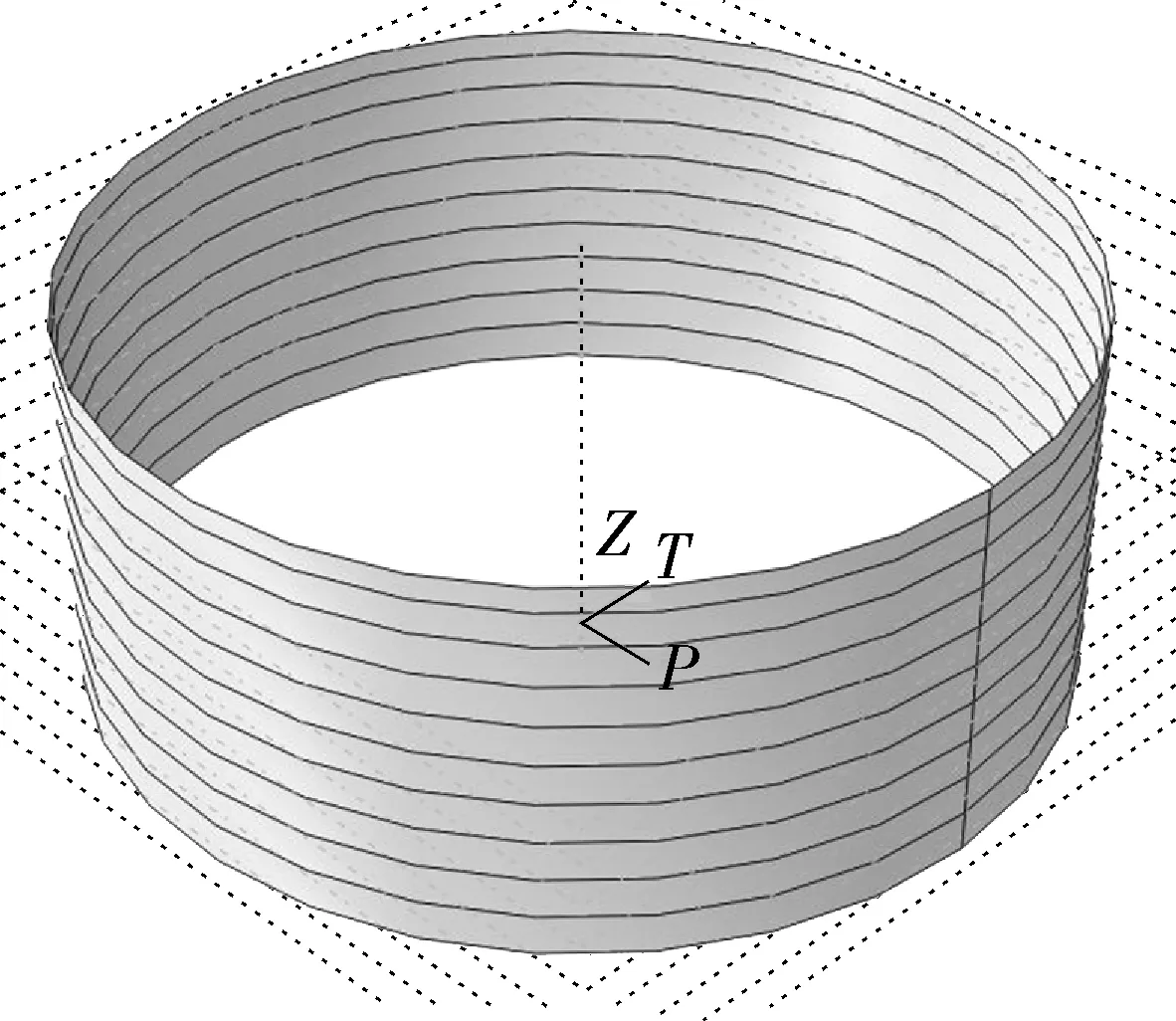
(a)几何模型 (b)网格划分

图4 储罐几何模型及网格划分

2.2 储罐仅在不均匀沉降下的屈曲分析

2.2.1 实测沉降数据处理

该固定顶储罐在罐壁底部沿周向均匀布置了12个沉降观测点，表3列出了某时刻各测点的实测沉降数值S。

表3 固定顶储罐沉降实测值

根据式(1),(2)，基于表3中的实测沉降数据，得到了储罐罐周的沉降曲线表达式如下：

S(θ)=2.0cos(2θ)+0.333cos(4θ)+1.73sin(2θ)

+1.15sin(4θ)+0.059cos(5θ)+1.47sin(5θ)

-1.33cos(3θ)-0.25cos(6θ)+4.83sin(3θ)

-20.7cos(θ)+11.9sin(4θ)+914.0

(6)

本文主要研究不均匀沉降U(θ)，故取式(6)中m≥2对应的项绘制沉降曲线,如图5所示。

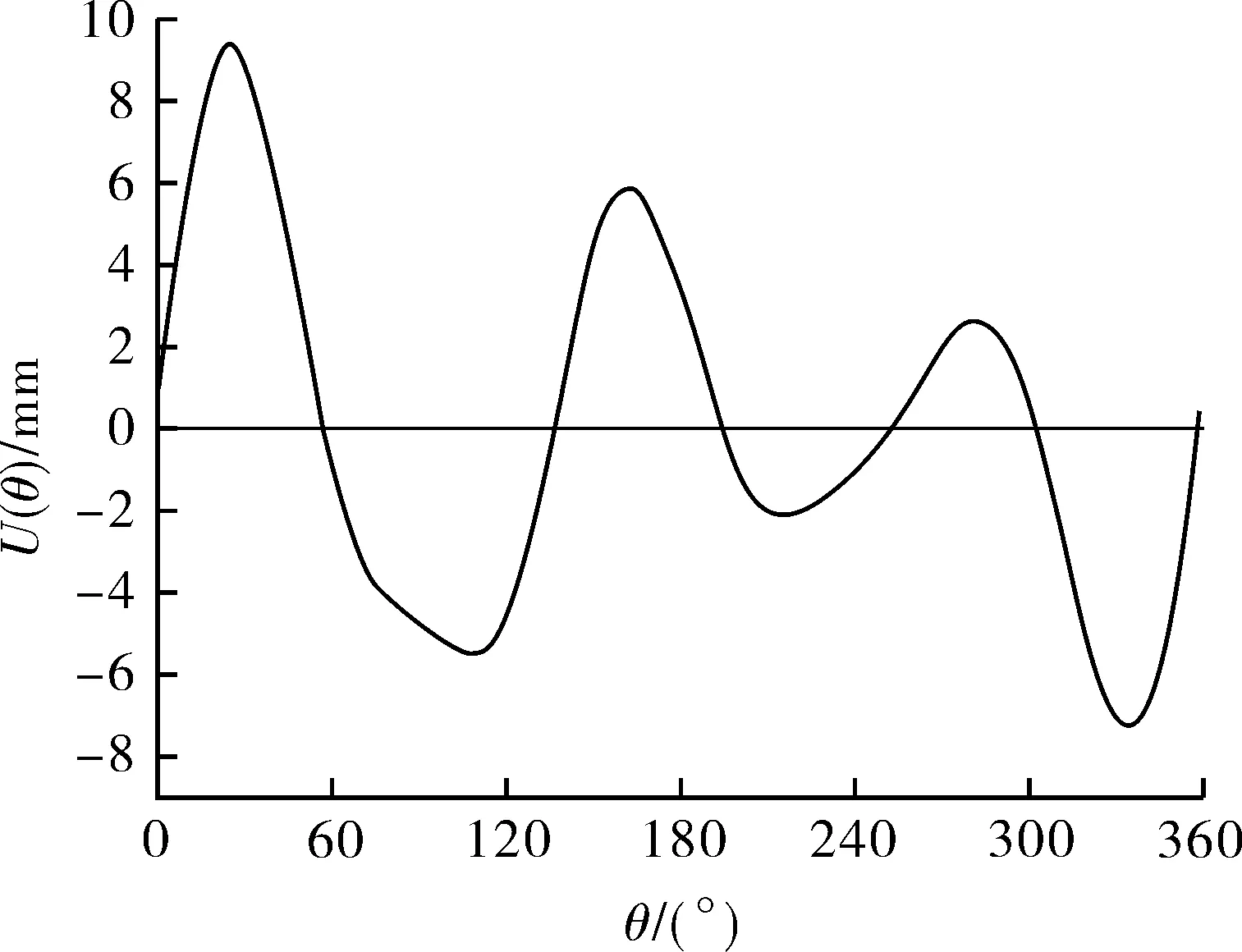
图5 储罐不均匀沉降曲线

图5中，U(θ)的正值表示储罐地基的向下沉降，U(θ)负值代表储罐地基的向上提离，不均匀沉降的最大幅值Umax=9.40 mm(向下)。绘制沉降沿罐周分布示意图，如图6所示(图中，曲线在储罐外侧表示向上提离，内侧表示向下沉降)。

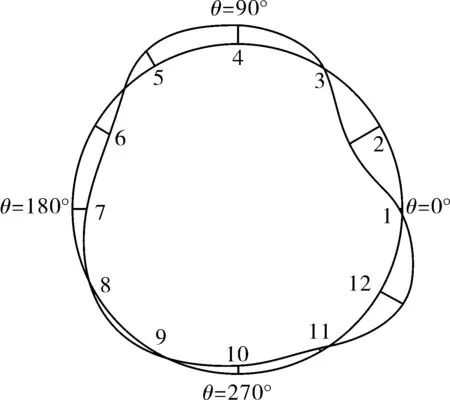
1～12-沉降观测点编号

2.2.2 屈曲计算

将U(θ)作为储罐底部的轴向位移边界条件，在ABAQUS软件中进行计算，得到储罐仅在实测不均匀沉降作用下的径向位移云图，如图7所示。

(a)LPFs=1 (b)LPFs=1.111

图7 储罐仅在不均匀沉降作用下的径向位移云图

从图7可以看出，当不均匀沉降完全加载时，即沉降比例系数LPFs=1时，储罐并未发生屈曲，结构处于稳定状态。但不均匀沉降使储罐罐壁上产生了较大的应力和变形，如图7(a)所示。储罐的径向位移记为r，当LPFs=1时，储罐最大径向位移rmax=61.19 mm，且发生位置恰好是不均匀沉降幅值最大的位置。结果表明，向上提离会使储罐产生向内的径向位移，向下沉降则造成向外的径向位移。

为了得到储罐在不均匀沉降作用下的屈曲临界值，假设不均匀沉降按照等比例的方式继续增大。绘制储罐上径向位移最大点的沉降-位移曲线，如图8所示。可以看出，在沉降加载初期，变形和沉降之间是线性关系；沉降增大到A点后，LPFs不再增加，结合图7(b)可以发现，在θ=0°附近出现了较大的变形和径向位移，说明储罐发生了结构的屈曲失稳破坏。此时LPFs=1.111，即Umax增大到10.44 mm(向下)时，储罐发生了屈曲。

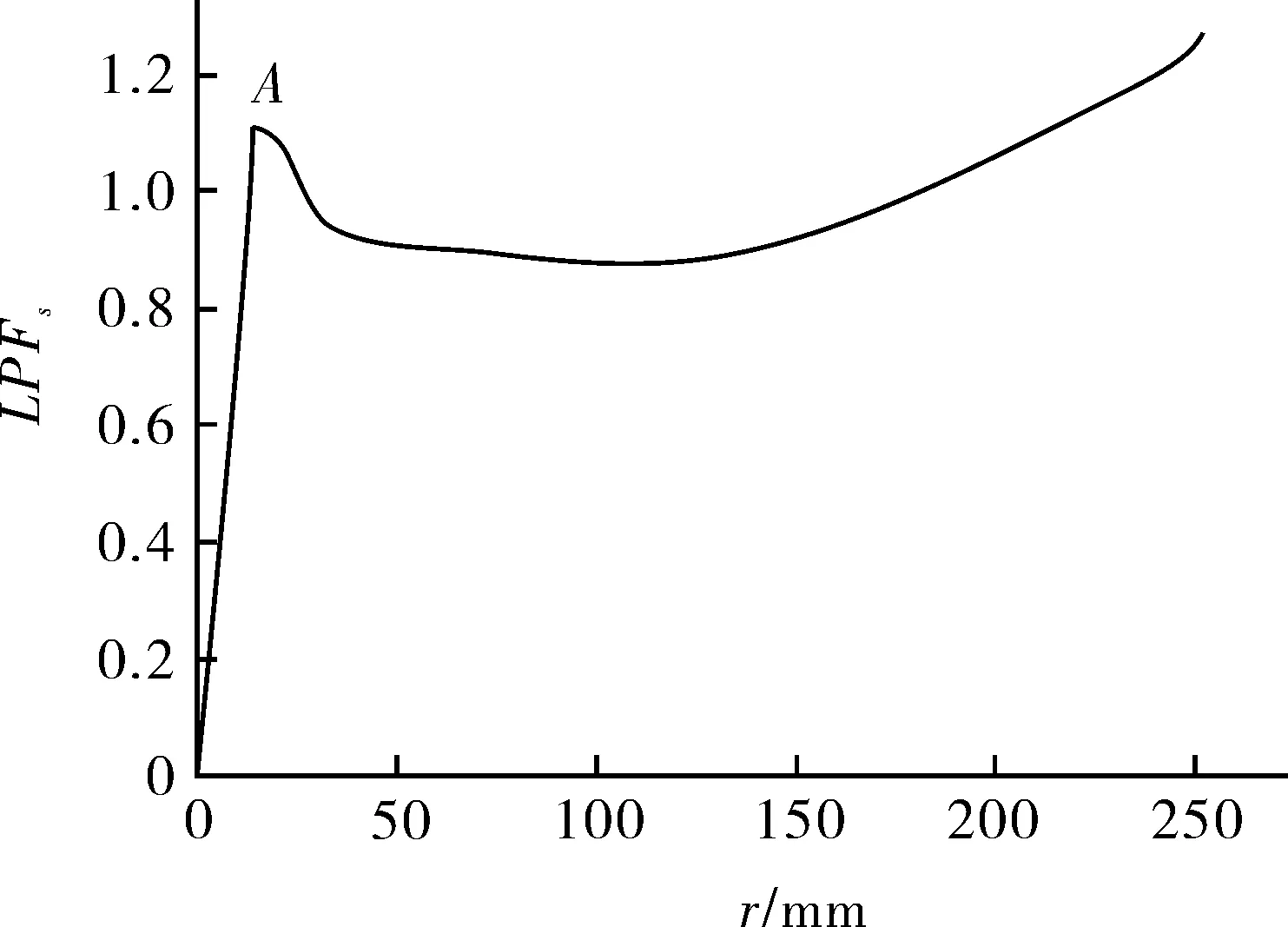
图8 储罐仅在实测不均匀沉降作用下的沉降-位移曲线

2.3 储罐仅在风载荷作用下的屈曲分析

根据GB 50009—2012《建筑结构荷载规范》查得舟山地区ω0=850 Pa，对应的风力等级为12级。根据式(4)，计算得到λ=1 985.6 Pa，将λ代入式(5)，即可得到沿罐周分布的风载荷分布形式。

(a)LPFw=1 (b)LPFwc=2.374

图9 储罐仅在风载荷作用下的径向位移云图(单位：m)

将风载荷分布函数施加于有限元模型。采用弧长法可计算得到储罐仅在风载荷作用下的变形响应，如图9所示，径向位移云图的正前方为储罐的迎风受压区(以下同)。当风载荷比例系数LPFw=1时，即风载荷完全加载，储罐发生了变形(见图9(a))。最大径向位移rmax=3.13 mm，结构处于稳定状态，且在迎风受压区，储罐产生向内的径向位移。

为了得到储罐在风载荷作用下的屈曲临界值，风载荷按照等比例的方式继续增大。储罐上径向位移最大点的载荷-位移曲线如图10所示。

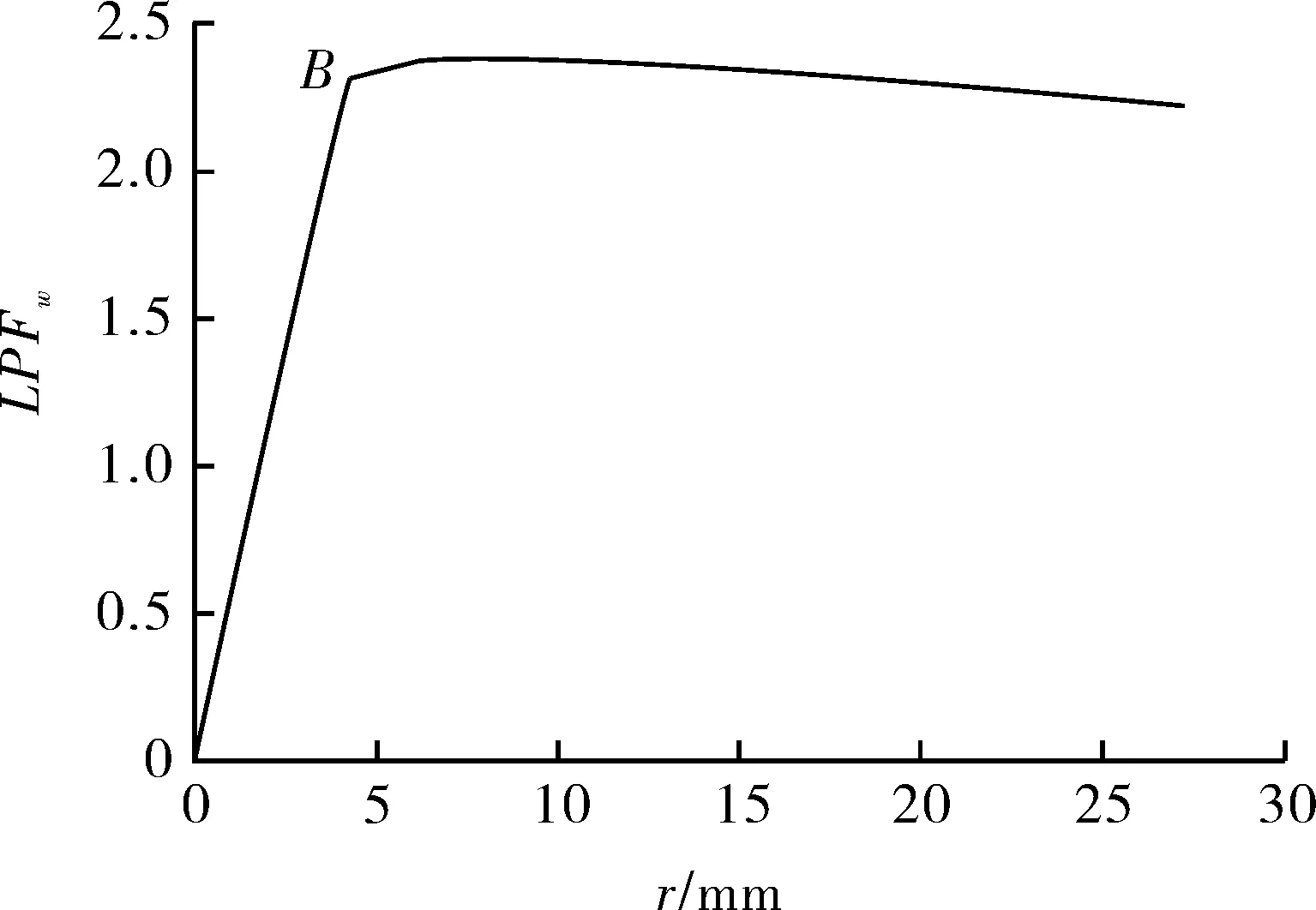
图10 储罐仅在风载荷作用下的载荷-位移曲线

可以看出，风载荷增大到B点后，LPFw不再增加，而径向位移迅速增大，储罐发生了屈曲失稳。将储罐发生屈曲失稳时的风载荷比例系数定义为临界风载荷比例系数，记为LPFwc,得到此时储罐的径向位移云图如图9(b)所示，屈曲出现在储罐的迎风受压区域。分析图10曲线，LPFw增大到B点时不再线性增大，即LPFwc=2.374，对应的λ=4 713.8 Pa，换算成风速v=56.8 m/s，风力等级Wc=17，为飓风。

2.4 联合作用下的屈曲分析

基于本文提出的两者联合作用下的屈曲分析方法，得到储罐径向位移云图，如图11所示。可以看出，屈曲发生的位置均在储罐的迎风受压区域。

(a)α=0°，LPFwc=0.323 (b)α=90°，LPFwc=1.317

在不同风向角的风载荷作用下，储罐径向位移最大点的载荷-位移曲线如图12所示。

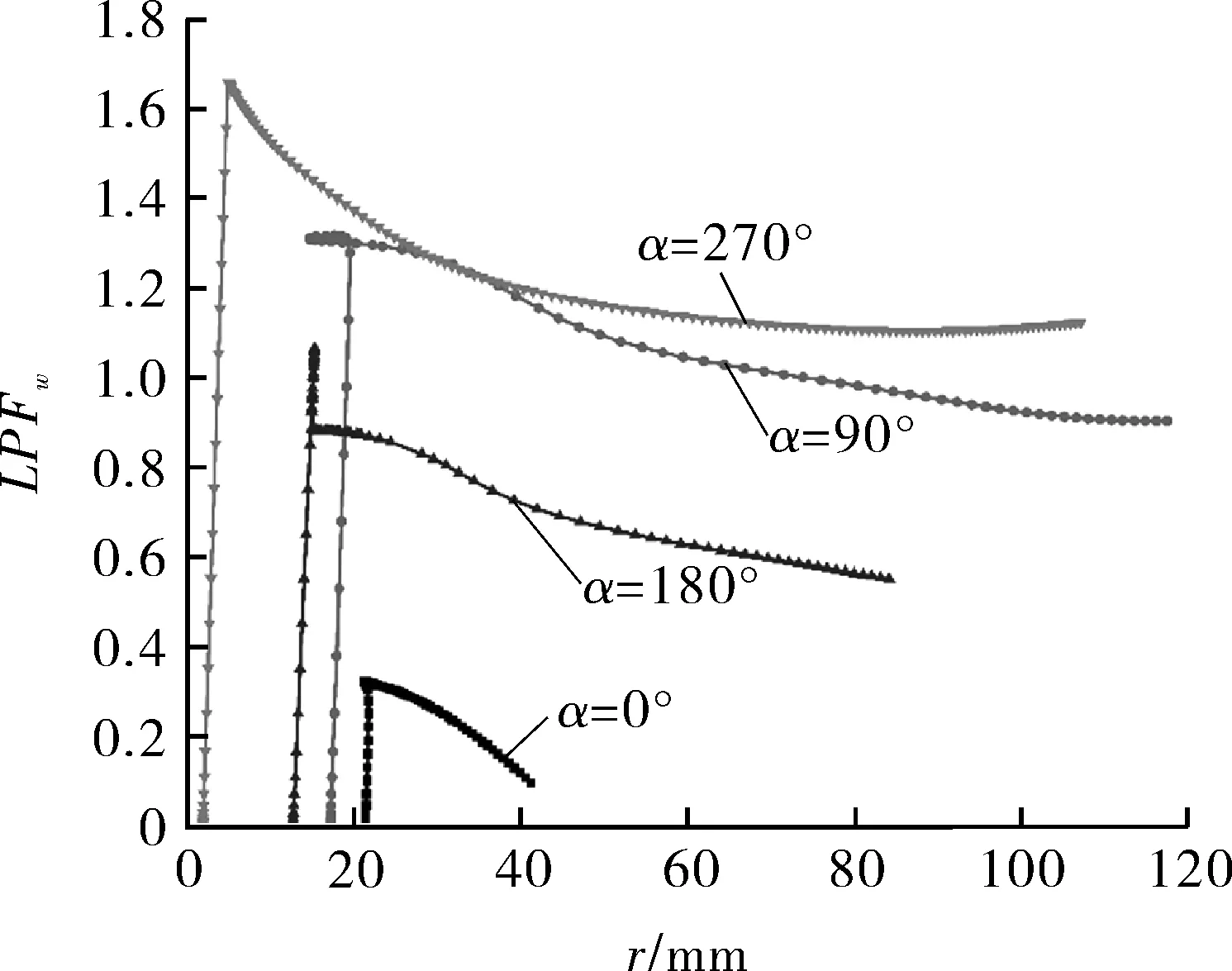
图12 不同风向角的风载荷-位移曲线

从图12可以看出，风载荷初始加载时，储罐的径向位移与风载荷呈线性关系。当风载荷增大到临界风载荷后，储罐的变形量迅速增大，发生了屈曲。由于沉降在罐壁底部分布的不均匀性，不同风向角风载荷的LPFwc差别较大。

相较于正常储罐发生屈曲时的LPFwc，将联合作用下各风向角风载荷临界比例数降低的百分比记为η，计算结果见表4。

结合表4和图12可以看出，α=0°时，具有不均匀沉降的储罐在风压幅值为640 Pa时发生了屈曲失稳，该值仅为舟山地区基本风压ω0对应风压幅值(1 985.6 Pa)的1/3。此时LPFwc=0.323，相比于无沉降的储罐，LPFwc降低了86.41%，仅在9级风作用下就会发生屈曲失稳。这是因为在不均匀沉降作用下，储罐在θ=0°的位置附近已经产生了较大的变形，严重降低了储罐的抗风稳定性。

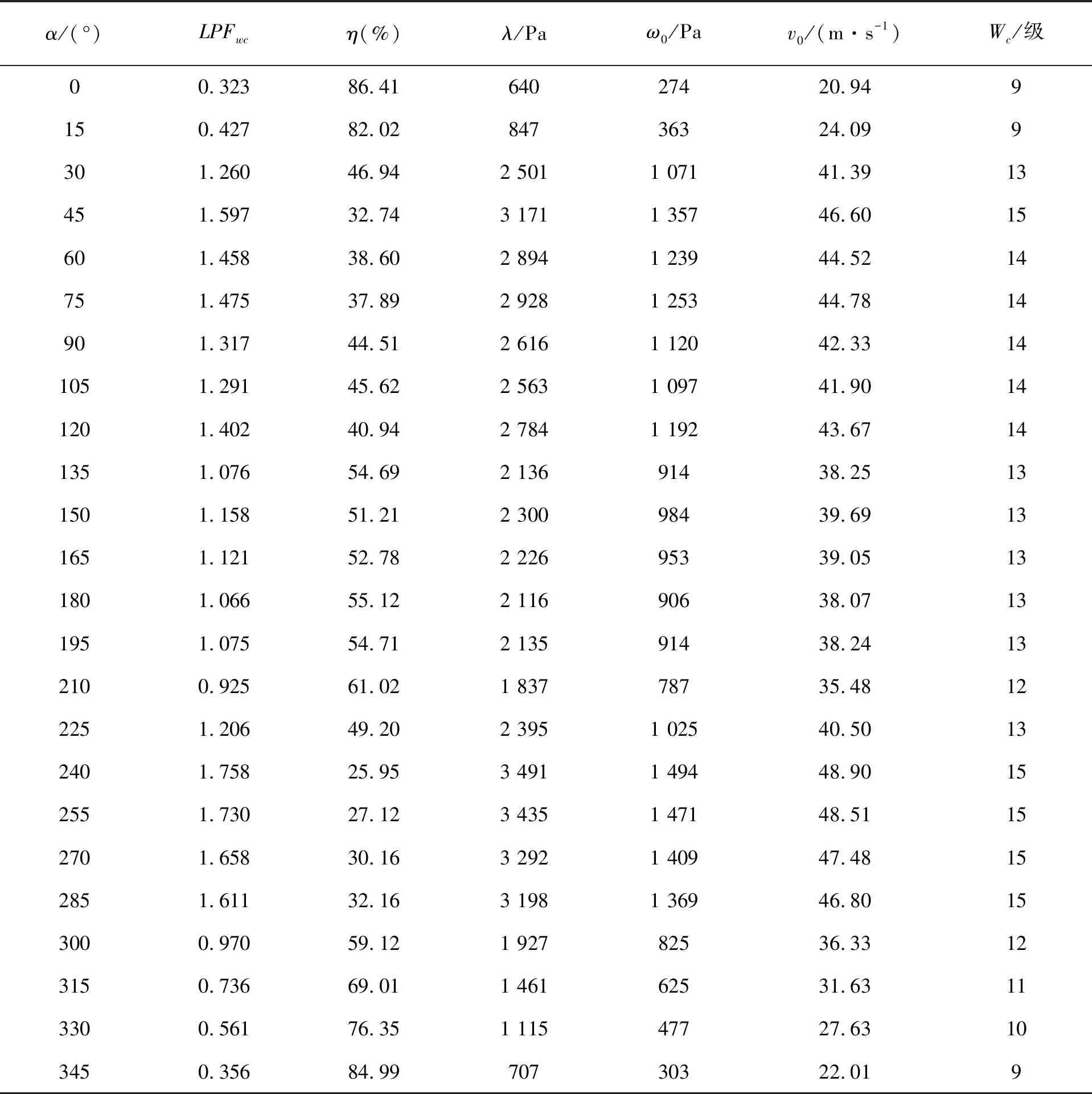
表4 不同风向角的临界风载荷

α在-60°～15°范围内时，对应的LPFwc<1.0，即风载荷幅值还未达到舟山地区的风压幅值1 985.6 Pa时就发生了屈曲失稳；而α在其余范围时，储罐发生屈曲时的LPFwc在1.0～1.8之间，对应的风力等级为13～15级，与前面计算得到的正常罐发生屈曲的17级风相比，风载荷的临界幅值下降较多。因而，不均匀沉降的存在，使储罐在风载荷作用下更易发生屈曲失稳。

根据表4计算结果，绘制储罐在各风向角风载荷作用下的LPFwc曲线，并将储罐实测的不均匀沉降曲线一并绘入，如图13所示，以对比分析不均匀沉降对储罐抗风性能的影响。

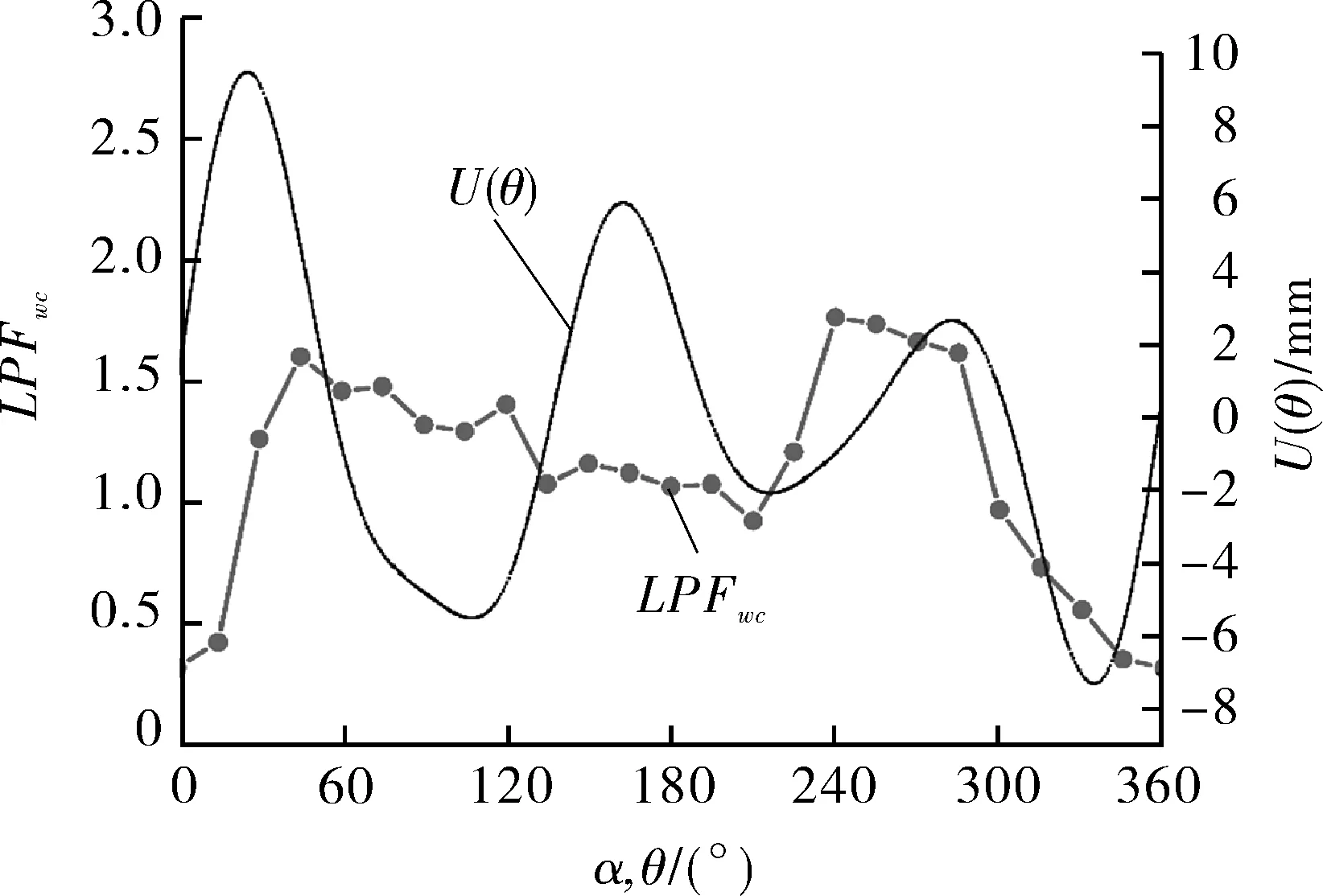
图13 各风向角风载荷的LPFwc曲线与不均匀沉降曲线

通过对比不同风向角风载荷的LPFwc曲线和不均匀沉降曲线发现，两条曲线(见图13)具有相似的变化趋势。在不均匀沉降向下沉降对应的罐壁区域，储罐的抗风稳定性削弱较少，这是因为地基的向下沉降会造成储罐向外的径向位移，但在风载荷作用下储罐的迎风受压区域会产生向内的径向位移，缓解了已有的变形；而在地基发生向上提离的区域，罐壁上产生了向内的径向位移，风载荷加剧了变形，因而在地基向下沉降对应的储罐罐壁抗风稳定性削弱较多，即不均匀沉降中的向上提离对储罐抗风稳定性更为不利。