气瓶内衬屈服强度对环缠绕复合气瓶疲劳性能影响的研究

2019-05-13由宏新

压力容器 2019年3期

由宏新

(1.中国船舶科学研究中心深海载人装备国家重点实验室，江苏无锡 214082；2.大连理工大学化工机械与安全学院，辽宁大连 116024；3.大连锅炉压力容器检验研究院，辽宁大连 116006)

0 引言

纤维缠绕的复合材料气瓶与全金属气瓶相比，具有质量轻、比强度高、抗疲劳性能好等优势，在海洋工程、舰船、航空航天、汽车等领域得到广泛应用，如呼吸系统用气瓶、航海救生筏充气用气瓶、车用压缩天然气气瓶等[1-2]。钢质内胆环缠绕(CNG-Ⅱ)复合气瓶作为复合材料气瓶的一种，是车用领域用于充装压缩天然气的关键部件。CNG-Ⅱ复合气瓶主要由金属内衬、纤维缠绕层组成，缠绕层纤维材料的承载能力远高于内衬金属材料[3]。因此，内衬工作时的受力状况、疲劳性能是决定环缠绕复合气瓶使用寿命长短的关键性因素[4]。

在探究复合气瓶的应力分布对气瓶疲劳寿命影响过程中，相关学者大多通过固定气瓶内衬材料的力学性能，优化气瓶的自紧压力[5]、缠绕张力[6]或气瓶内衬结构[7]，得到最佳抗疲劳性能。刘培启等[8-9]从考察内衬工作压力下所受应力幅与环向平均应力出发，研究自紧压力对气瓶疲劳寿命的影响，得出自紧压力增大引起的环向平均应力降低是提高气瓶抗疲劳性能的主因。苏镜元[10]将缠绕张力等效为内胆的当量外压力，采用逐层缠绕方法，通过有限元分析发现缠绕张力能够对气瓶内胆产生预应力，较小的缠绕张力能够改善气瓶的应力分布。李清婉等[11]研究表明，内胆壁厚增加，能够小幅度提高环缠绕复合气瓶的抗疲劳性能。

然而，在自紧压力、气瓶结构尺寸固定的情况下，内衬屈服强度的高低决定气瓶在自紧后残余压应力的大小，将直接影响复合气瓶内衬在工作压力下的应力水平，从而间接影响复合气瓶的疲劳性能[12-15]。Veys等[16]系统研究了内衬材料发生塑性变形时，铝内衬的复合材料容器的疲劳寿命。周丹等[17]在相同结构、预紧力与工作压力下，分析比较了两种不同型号的铝合金材料作为内衬的复合气瓶的受力状况，得出内衬材料的力学性能不同是导致气瓶应力分布差异的原因的结论。Burov等[18]发现，内衬材料的力学性能对内衬及复合缠绕层的受力状况、缠绕层的高强度特性的发挥有显著影响，决定容器的承载极限能力与疲劳寿命。

本文利用有限元数值分析方法，以外径406 mm的环缠绕复合气瓶为研究对象，保持气瓶结构尺寸不变，固定自紧压力和内衬抗拉强度，考察内衬屈服强度变化条件下，气瓶内衬与缠绕层在不同工况下的应力分布情况，并分析屈服强度变化对气瓶疲劳寿命的影响规律。在此基础上，对内衬外径分别为406,356,325 mm的3种规格尺寸的环缠绕复合气瓶在不同内衬屈服强度下进行疲劳试验，将试验结果与有限元数值模拟进行对比，以验证数值分析的可靠性。

1 有限元计算模型

1.1 几何模型

选取的环缠绕复合气瓶模型如图1所示。气瓶容积90 L，内衬公称外径406 mm，内衬壁厚5.6 mm；纤维层厚0.29 mm，层数24，缠绕层总厚度6.96 mm。气瓶其余部位尺寸见图1。

图1 气瓶模型结构尺寸

1.2 材料特性

气瓶内衬材料选取30CrMo，复合材料缠绕层采用玻璃纤维158B-AB-450。表1列出内衬和复合层纤维材料力学性能参数，表2列出玻璃纤维158B-AB-450的各向性能参数。图2示出气瓶内衬的真实应力-应变(σ-ε)曲线。

表1 内衬和复合层纤维材料力学性能参数

表2 158B-AB-450玻纤/环氧树脂复合材料各向性能参数

注：Ei,υij,Gij-下标方向的弹性模量、泊松比、剪切模量

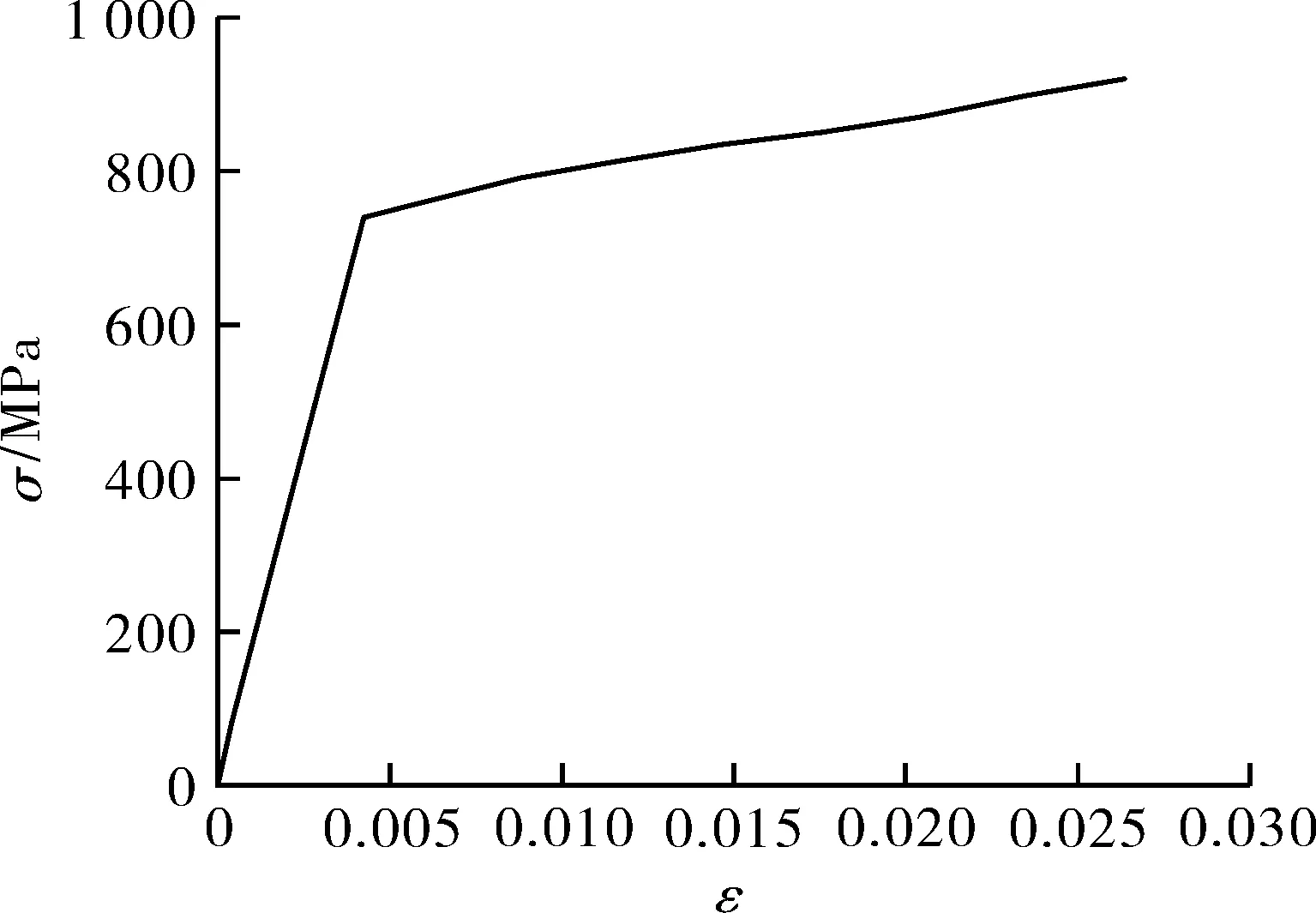
图2 30CrMo钢的真实应力-应变曲线

文中针对考察的内衬的不同屈服强度这一参数，可通过对内衬进行调质热处理时，改变回火时的回火温度和回火保温时间(或回火工艺)，调节不同的力学性能，且假设经过热处理只改变材料的屈服强度，不改变材料的抗拉强度。

1.3 网格模型

由于气瓶在几何尺寸与载荷条件上的轴对称性，本文在对复合气瓶有限元建模时，建立1/4模型进行计算分析。内衬采用8节点Solid 45单元，复合材料层采用4节点Shell 181单元。其中，假设内胆与纤维缠绕层及纤维缠绕层各层间粘结牢固，无滑移。通过设置内衬外表面Solid 45单元的节点与纤维缠绕最内层Shell 181单元的节点相耦合来实现该假设[19]。网格划分后得到环缠绕复合气瓶共有21 280个单元，其中Solid 45单元有18 480个，Shell 181单元有2 800个。图3示出建立的环缠绕复合气瓶有限元网格。

图3 气瓶有限元网格

1.4 边界条件与载荷

在建立的1/4气瓶模型中，对剖面施加对称约束，底部施加位移约束。载荷的加载过程为多载荷步进行连续施加计算，各载荷步对应相应工况，内压载荷P依次为自紧压力、自紧卸载后零压、工作压力、最小爆破压力。表3列出各工况下内压载荷P设定值。具体施加时，在气瓶内壁施加各工况下的压力P，同时在气瓶的接嘴端面施加等效拉应力F。F的计算公式为：

(1)

式中F——气瓶接嘴端面的等效拉应力，MPa；

di，do——瓶口内、外径,mm;

P——气瓶内压载荷，MPa。

表3 气瓶内压载荷P设置 MPa

2 屈服强度对气瓶应力的影响

在复合气瓶的实际生产中，可通过改变调质热处理过程中的回火处理工艺参数，调节内衬的屈服强度[20]。文中在固定内衬材料强度极限920 MPa下，研究内衬材料屈服强度σs的变化对复合气瓶内衬和纤维缠绕层应力的影响。有限元模拟计算中，在内衬屈服强度σs为730～870 MPa区间内，选取不同的内衬屈服强度值(730，750，770，790，810，830，850，870 MPa)进行计算，考察复合气瓶的内衬与缠绕层在各工况下的应力分布情况。

在一系列计算结果中，选取内衬屈服强度分别为730 MPa与870 MPa时的计算结果，进行比较分析。图4示出屈服强度730 MPa和870 MPa下，气瓶在自紧卸载后零压下内衬的残余压应力σ1对比云图。可以看出，不同屈服强度下，气瓶内衬应力分布规律基本类似；封头区域、部分封头与筒体连接区域呈环向预拉伸应力状态，筒体主要区域呈残余压应力状态。不同点在于，屈服强度730 MPa下，筒体主要区域的残余压应力为184.07 MPa，而屈服强度870 MPa的筒体主要区域的残余压应力只有25.27 MPa。

(a)σs=730 MPa (b)σs=870 MPa

图4 内衬屈服强度不同时卸载后零压下内衬的残余压应力σ1对比

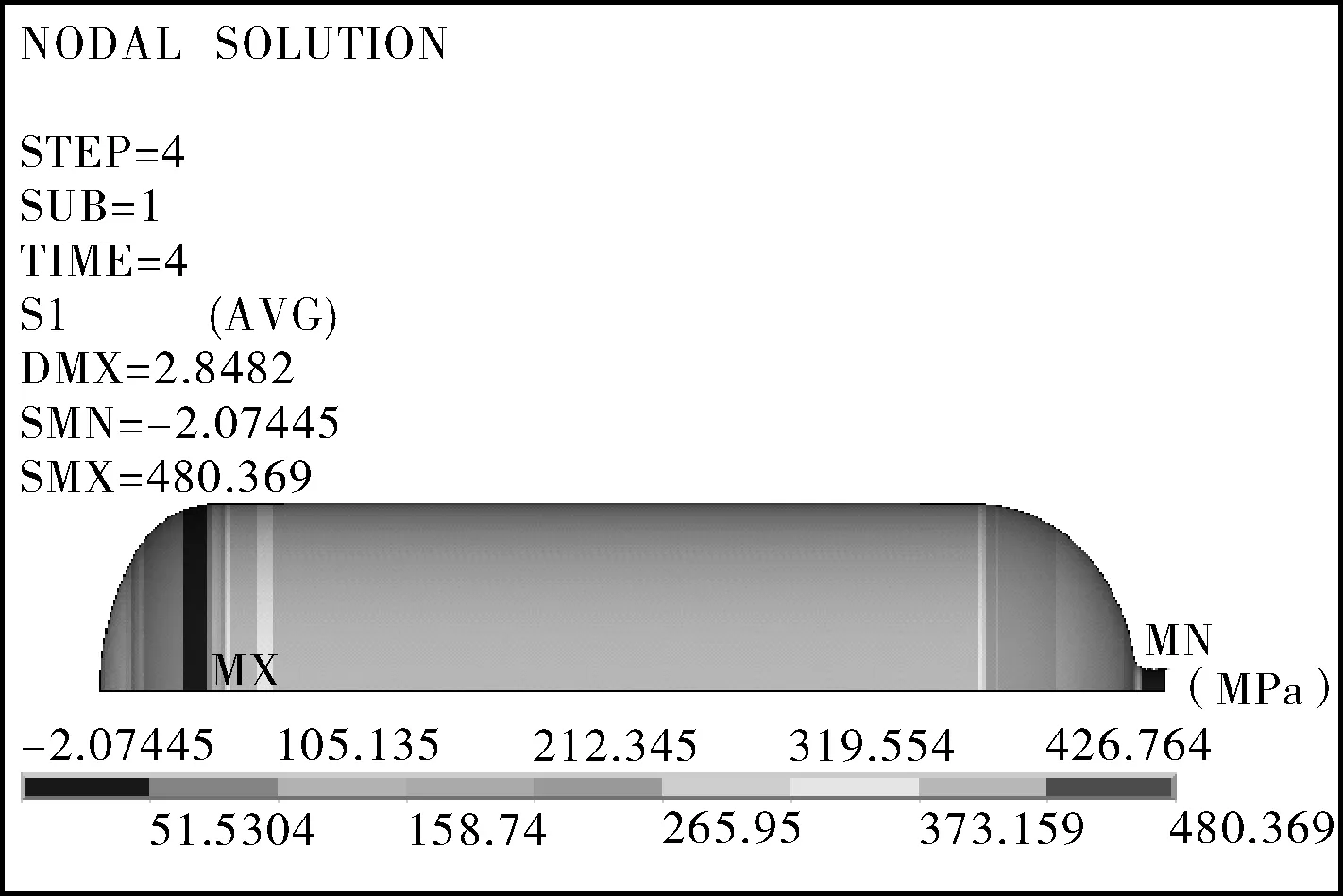
图5示出气瓶在工作压力下内衬的环向应力σ2对比云图。

注：σm1-自紧压力下内衬的Mises应力；σ1-卸载后零压下内衬的残余压应力；σ2-工作压力下内衬的环向应力；σm2-最小爆破压力下内衬的Mises应力；σ3-工作压力下纤维层的环向应力；σ4-最小爆破压力下纤维层的环向应力；fsr-纤维应力比

从图5可以看出，不同屈服强度下，气瓶内衬环向应力分布规律基本类似。然而，受自紧卸载后内衬的残余压应力的不同影响，屈服强度730 MPa下，环向应力最大值出现在筒体与封头连接处，筒体区域的环向应力值分布在373.16～426.76 MPa之间；而屈服强度870 MPa下，环向应力最大值出现在筒体处，筒体的环向应力值分布在496.54～558.56 MPa之间。这与图4中气瓶在自紧卸载后零压下内衬的残余压应力分布情况相对应。

在其余屈服强度条件下，气瓶内衬的应力分布情况与图4，5基本类似。表4列出8组不同屈服强度值下，气瓶内衬与纤维缠绕层在不同工况下的应力值的计算结果。

2.1 屈服强度对气瓶自紧效果的影响

依据表4中计算结果，图6示出了自紧压力下内衬的Mises应力σm1随屈服强度σs的变化曲线，以及气瓶自紧效果σ1-s随屈服强度σs的变化情况。

(a)自紧压力下内衬的Mises应力 (b)自紧效果σ1-s

图6 自紧随屈服强度σs变化曲线

由图6(a)可以看出，随内衬屈服强度增加，自紧压力下内衬的Mises应力值变大，内衬屈服强度从730 MPa增大至870 MPa的过程中，内衬Mises应力从773.56 MPa增大至873.32 MPa。在内衬不同屈服强度下，内衬的最大Mises应力均已超过材料的屈服极限，内衬处于塑性应力状态。

为了考察内衬屈服强度变化对自紧效果的影响，定义参数自紧效果σ1-s。σ1-s为自紧压力下内衬Mises应力与相应的屈服强度的差值，代表自紧卸压过程中，内衬受压屈服后的应力的大小，差值越大，表明受压效果越好。在图6(b)中，σ1-s随屈服强度的增大而减小,内衬Mises应力与屈服强度的差值σ1-s从43.56 MPa减小至3.33 MPa，表明随着内衬屈服强度增大，气瓶的自紧效果变差。

2.2 屈服强度对气瓶内衬应力的影响

图7示出复合气瓶内衬在自紧卸载后的残余压应力σ1和工作压力下的环向应力σ2随屈服强度σs的变化情况。

由图7(a)可看出，随内衬屈服强度增加，内衬在自紧卸载后零压下的残余压应力减小；在图7(b)中，内衬在工作压力下的环向应力随内衬屈服强度增加而增大。在屈服强度从730 MPa增大至870 MPa过程中，内衬在自紧卸载后零压下的残余压应力从208.19 MPa减小至78.93 MPa；而在工作压力下内衬的环向应力却从480.36 MPa增大至558.56 MPa，内衬屈服强度增加19.2%，内衬残余压应力水平减小达到62.1%，工作压力下内衬环向应力水平增加16.3%。环向应力增加速率明显低于残余压应力的减小速率，其原因是随着内衬材料的屈服强度增大，气瓶的整体应力水平增加速率下降，一定程度上降低内衬的工作应力水平增加速率[11]。但气瓶所受残余压应力减小，自紧效果变差，内衬在工作压力下会承受更多的拉应力，易导致气瓶的疲劳寿命降低。

(a)卸载零压下内衬残余压应力σ1(b)工作压力下内衬环向应力σ2

图7 内衬应力随屈服强度σs变化曲线

2.3 屈服强度对气瓶纤维缠绕层应力的影响

图8示出复合气瓶在工作压力下纤维缠绕层的环向应力σ3，以及最小爆破压力下纤维缠绕层的环向应力σ4随屈服强度σs的变化情况。可以看出，在工作压力与最小爆破压力下，随着内衬屈服强度的增加，纤维缠绕层的环向拉应力均减小。在内衬屈服强度从730 MPa增大至870 MPa的过程中，纤维缠绕层在工作压力下的环向应力从265.69 MPa减小至155.79 MPa，而在最小爆破压力下的环向应力从785.88 MPa减小至765.81 MPa，纤维应力比从2.96增大至4.92。从纤维层利用角度，纤维层承受载荷减小，纤维的高强度特性未能得到有效发挥，使气瓶内衬承受更多环向拉应力，一定程度上降低了气瓶的疲劳寿命。

(a)工作压力下纤维缠绕层环向应力σ3(b)最小爆破压力下纤维缠绕层环向应力σ4

图8 纤维缠绕层应力随屈服强度σs变化曲线

3 屈服强度对气瓶疲劳寿命的影响

缠绕层纤维材料的疲劳寿命远高于内衬金属材料的疲劳寿命，因此，内衬的疲劳性能是影响环缠绕复合气瓶的决定性因素。而内衬工作时的应力幅和环向平均应力是影响气瓶内衬疲劳寿命的关键因素。文中取自紧后零压力下的内胆环向最大压应力节点318作为分析对象，分析内衬屈服强度变化对应力幅和环向平均应力的影响[9]。当内衬屈服强度由730 MPa增加到870 MPa时，计算318节点的应力幅σs，a和环向平均应力σa，s，其结果如表5所示。内衬的应力幅σs，a和环向平均应力σa，s计算公式如下：

σs，a=(σmax-σmin)/2

(2)

σa，s=(σmax+σmin)/2

(3)

式中σmax——内衬在工作压力下的应力，MPa；σmin——内衬在卸载零压下的应力，MPa。

表5 318节点的σs，a与σa，s随内衬屈服强度的变化结果 MPa

图9示出318节点的σs,a和σa,s随内衬屈服强度的变化曲线。

图9 σs，a和σa，s随屈服强度σs变化曲线

从图9可以看出，当内衬屈服强度从730 MPa增加到870 MPa时，内衬的应力幅几乎保持不变；然而，内衬受到的环向平均应力逐渐增加。内衬屈服强度从730 MPa增加至870 MPa，环向平均应力增幅达到2.55倍。研究表明，内衬应力幅保持一定时，气瓶的疲劳寿命会随内衬所受环向平均应力增加而降低[9]。因此，随内衬屈服强度的增加，气瓶内衬的疲劳寿命将降低。

4 气瓶疲劳试验数据验证

为验证上述分析的正确性，对不同屈服强度的调质30CrMo内胆环缠绕气瓶进行疲劳试验。试验采用符合GB/T 9252—2017[21]疲劳试验要求的装置，根据GB 24160—2009[22]的要求，进行疲劳试验。试验压力范围为2～26 MPa，试验过程中温度控制在低于50 ℃。疲劳试验过程中气瓶的失效，都是气瓶内胆疲劳引发的泄漏。图10示出外径406 mm和356 mm气瓶疲劳试验过程中失效的现象。

(a)外径406 mm (b)外径356 mm

图10 气瓶疲劳试验过程中的失效现象

内衬外径406 mm的气瓶最低疲劳次数与相关的材料屈服强度见表6。

表6 CNG2-G-406-100-20B缠绕气瓶不同屈服强度下的疲劳试验次数

由表6的数据分析可知，在4组试验中，当气瓶内衬的屈服强度不大于795 MPa时，气瓶的循环次数超过45 000次，符合GB 24160—2009[22]要求;当气瓶的内衬屈服强度进一步增加，气瓶的疲劳循环次数随着屈服强度的增加而减小，即复合气瓶的寿命随着内衬屈服强度的增加而减小。

为进一步验证相关分析的正确性，又对内衬外径356 mm与325 mm的气瓶进行疲劳试验，试验条件与内衬外径406 mm气瓶相同。相关的试验结果见表7,8。

由表7,8可以看出，在内衬外径为356 mm和325 mm气瓶的试验中，当气瓶内衬的屈服强度分别不大于790 MPa和824 MPa时，气瓶的循环次数均超过45 000次，符合GB 24160—2009要求。与内衬外径406 mm气瓶类似，当气瓶的内衬屈服强度继续增加时，气瓶的疲劳循环次数减少，复合气瓶的寿命降低。