PSO-无偏灰色马尔科夫模型在船舶交通流量预测中的应用

马全党， 江福才， 范庆波， 朱蓉蓉

(武汉理工大学 a.航运学院;b.内河航运技术湖北省重点实验室， 武汉 430063)

伴随着我国经济的发展，尤其是“一带一路”政策的实施，加速了水上交通运输的发展，船舶数量逐渐增多，船舶大型化和高速化趋势日益明显。[1-2]船舶交通流量的准确预测，可让港口部门根据船舶交通流的变化规律，科学合理地规划水域布局，提高航道的通航效率,同时也为海事管理部门提供基础性数据，更好地保障通航安全。[3]

目前国内外的学者在船舶交通流量预测方面主要有定性预测和定量预测两大类。

1) 定性方法主要指经验判断性质的分析预测，具有代表性的方法有“头脑风暴法”“德尔菲法”和“广义德尔菲法”[4]等，这些方法包含很强的主观因素，误差较大且预测精度不高。

2) 定量预测是指运用数学模型进行预测，目前应用比较广，例如：运用线性增长模型[5]、径向基函数(Radical Basis Function,RBF)神经网络模型[6]等。

本文主要就灰色模型、马尔科夫模型、粒子群算法应用情况进行介绍。马晓波等[7]运用灰色系统预测模型，引入残差修正等方法优化模型，对长山水道2015—2016年船舶交通流量进行预测。郑友银等[8]运用灰色模型与自回归模型结合，对港口的船舶交通流量进行预测等；灰色模型可提高样本数量和信息少的数据的预测精度，但对波动性大的数据预测精度低，且未消除指数偏差。吕鹏飞等[9]利用BP(Back Propagation)神经网络与马尔科夫模型结合，将残差划分状态，白化系数取0.5，用马尔科夫修正神经网络预测值的方法对长江九江大桥的月度船舶交通流量进行预测；马尔科夫模型对残差序列区间进行白化，一般选取状态区间的中间值，白化系数为0.5，不具有普适性，误差较大。李松等[10]应用粒子群算法所具有的全局搜索能力对BP神经网络进行优化，辅助求解最佳的权值和阈值，提高交通流量的预测精度。许多学者已将无偏灰色模型、马尔科夫模型、粒子群算法应用到煤矿、道路交通和降水等领域，取得很好的预测效果。

鉴于以上分析，本文在无偏灰色模型的基础上，引入马尔科夫模型，弥补无偏灰色模型在对波动性大的数据，预测精度低的不足，并运用PSO优化算法，自适应求取最佳白化系数，应用该方法对东营港2012—2017年船舶交通流量季度统计数据进行拟合与预测，以期得到最佳的预测效果。

1 构建PSO-无偏灰色马尔科夫链模型

1.1 无偏灰色模型

在生活中，存在很多系统的信息为部分已知但并不全知，称为灰色系统，灰色模型就是对灰色系统进行预测，虽然系统表现的现象是随机的、杂乱无章的，但依然具备一定的潜在规律。灰色模型就是寻找这种规律并加以利用，从而进行预测。[11]选择灰色模型中的GM(1,1)进行预测，灰色模型GM(1,1)在原始时间序列隐含着指数变化规律时预测误差较小。传统的灰色模型GM(1,1)在构建序列模型步骤过于繁琐，为方便计算，构建无偏灰色GM(1,1)模型，建模步骤如下：

构建原始序列为

X(0)(k)=(X(0)(1),X(0)(2)，…X(0)(k))=

(1)

1) 对原始序列作一阶累加，生成数据累加序列和一阶线性微分方程为

(2)

(3)

2) 为得到待定参数的解，构建矩阵Bn,Yn为

(4)

3) 用最小二乘法计算线性微分方程的参数a和μ。

x(0)(k)=-aZ(1)(k)+μ

(5)

(6)

(7)

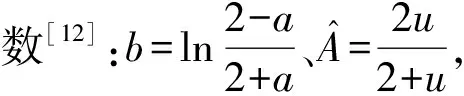
(8)

1.2 无偏灰色马尔科夫模型

马尔科夫模型是一个随机变量序列，它与某个系统的状态相对应，而此系统在某个时刻的状态只依赖于它的前一时刻的状态，该模型[13]表示为

X(n)=X(k)Pn-1

(9)

(10)

残差序列e(i)存在规律性，应对残差序列利用马尔科夫模型来修正。将残差序列按照大小划分为间隔宽度相等的r个状态，残差序列F(i)的第i步的第j个状态的上下边界分别用Hij和Qij表示，计算方法[13]为

(11)

(12)

设状态空间为I={i1,i2,…,ir}，在每一个时间点，随机过程中的每一个值只能处于一种状态，每个状态在接下来的状态转移有r个转向(包括转向自身)，即：{ii→i1,ii→i2,…,i→ir}。从状态i经过一步状态转移到状态j的概率为

∀i,j∈I。

(13)

同理可得到k步状态转移概率为

∀i,j∈I

(14)

进而构建能反映系统间各状态概率转移的一步转移矩阵为r×r。[14]该转移矩阵为

(15)

从状态转移矩阵的行向量里可得到无偏灰色模型残差序列里某序列值经过一步状态转移的概率，记为ai(t)(i=1,2,3,…,r)，转移时间用T表示。选取r个状态区间，每个状态区间的中间值为该区间可能的预测值，用zi(i=1,2,3,…,r)表示，通常取0.5，得到预测结果的表达式为

(16)

1.3 PSO优化

在以上建模过程中，zi(i=1,2,…,λ)取状态区间的中间值(白化系数为0.5)，该值不具有普适性且误差较大。本文引入粒子群算法对上述模型进行优化，根据数据序列的变化规律，求取最佳的白化系数。

将得到的状态区间看作为一个灰区间，对这种灰区间进行白化的方法为

(17)

KENNEDY等[15]提出粒子群算法，这是一种模拟鸟群社会性的多点搜索方法，具有全局搜索能力强、过程简洁和参数少的特点，用以自适应选取最佳白化系数。

vi(t+1)=wvi(t)+c1rand1(xpbesti-xi(t))+

c2rand2(xgbesti-xi(t))

xi(t+1)=xi(t)+vi(t+1)

(18)

式(18)中：xi为在t时刻的位置;vi为粒子在t时刻的速度;xpbesti为群体搜索到的最佳位置;xgbest为粒子全体极值经历的最好位置；rand1、rand2为服从U(0,1)的随机数;ω为惯性系数;c1、c2为加速度系数。

用均方差fit来衡量每个粒子的适应度函数

(19)

PSO-无偏灰色马尔科夫模型的建模步骤见图1。

图1 PSO-无偏灰色马尔科夫模型计算步骤

1.4 模型检验

为定量评价模型的船舶交通流量预测结果，综合采用平均绝对误差(Mean Absolute Error,MAE)和平均绝对百分误差(Mean Absolute Percentage Error,MAPE)[14]对预测精度进行计算。

MAE的计算公式为

(20)

MAPE的计算公式为

(21)

MAE与MAPE分别反映原始值与预测值的平均偏离程度及模型预测数据的拟合程度,值越小，越能反应预测值的准确性与可靠性。

2 算 例

2.1 数据样本的选取

标准船舶的选取是为方便对不同水域相同时段或同一水域不同时段的船舶交通流量进行统计、更好地表征船舶交通流的概念。文献[16]提到标准船舶作用有：实现不同航段船舶交通流量的比较，反映不同航段船舶交通流量的特点。日本运用“L系数”“L2系数”的方法确定标准船舶，我国采用如下换算系数将原始数据转化为标准船舶数据[13],见表1。

表1 标准船舶换算系数表

为保证预测数据的准确性，在东营海事局的配合下利用船舶签证原始资料统计得到东营港2012—2017年共23个季度的船舶交通流量。根据以上换算系数，对原始数据进行标准船舶转换，得到的标准船舶见表2。

表2 东营港2012年1月—2017年9月船舶交通流量季度统计表 标准船/艘次

2.2 无偏灰色模型预测

根据表2，拟选择前21个样本数据作为拟合数据，建立非负原始数据序列为

(22)

依据无偏灰色模型的建模步骤，运用MATLAB R2014a软件编制无偏灰色模型程序计算，得到

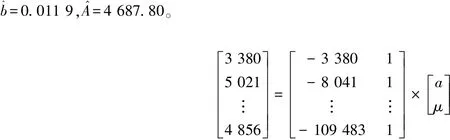
(23)

(24)

应用MATLAB R2014b，参照式(4)得到无偏灰色模型的预测值。

2.3 无偏灰色马尔科夫模型预测

依据上文无偏灰色马尔科夫模型的建模流程，确定残差序列的范围e(i)∈[-1 562.93,1 284.68]。将残差序列划分为4个状态区间，区间的上下边界值如下：

状态E1为

同理得到E2、E3、E4状态的上下边界区间分别为[-851.02,-139.12]、[-139.12,572.77]、[572.77,1 284.68]。无偏灰色模型残差序列状态分布见表3。

表3 无偏灰色模型残差序列状态分布表

根据表3状态的分布情况，对从Ei经一步转移到Ej的频数统计见表4。进而得到状态转移概率矩阵为

(27)

计算4个状态区间的中间值：z1=-1 211.71,z2=-489.24,z3=233.24,z4=955.71。根据式(16)得到无偏灰色马尔科夫模型的预测结果，见表5。

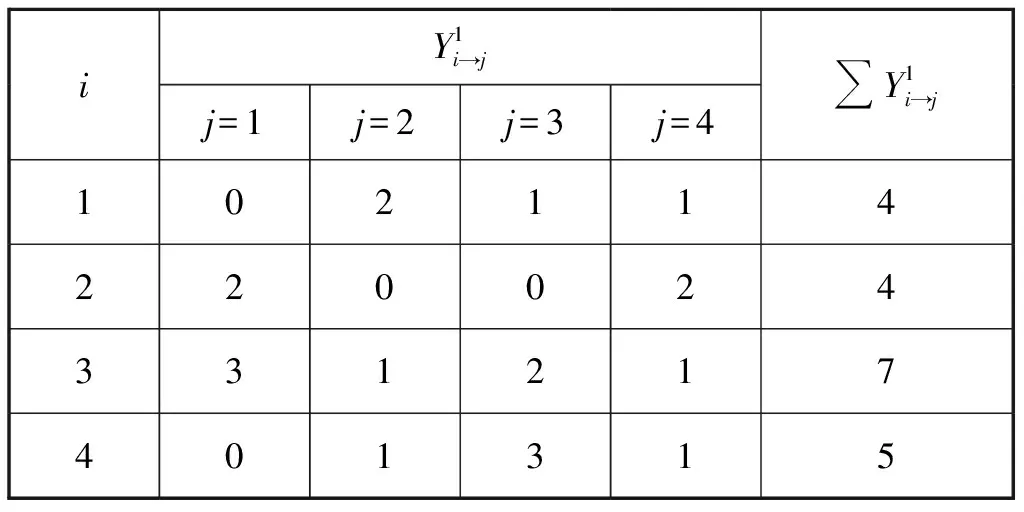
表4 一步状态转移频数统计表

表5 模型预测结果及残差

2.4 PSO优化

粒子群算法全局搜索能力强，综合考虑残差序列、状态区间和状态转移概率等，能够帮助寻找到最佳的白化系数。运用式(17)得到

(28)

(29)

(30)

(31)

根据以上的计算结果，现将无偏灰色模型、无偏灰色马尔科夫模型、PSO-无偏灰色马尔科夫模型船舶交通流量预测值和残差汇总如表5所示。

船舶交通流量预测值结果对比见图2。无偏灰色模型的预测值从第2季度开始为单调递增的光滑直线，样本实际值基本位于直线两侧，该模型对单调递增的数据预测精度高，对受到多种因素影响的波动性较大的数据预测精度较低。无偏灰色马尔科夫模型拟合效果不好，原因在于该模型白化系数值为0.5，即选择的每个状态区间的中间值为该区间的可能值，但在实际中，中间值并不一定是最优解。运用PSO算法进行全局搜索，寻找到最佳的白化系数，弥补了马尔科夫模型在白化系数选取上的不足，拟合效果较好，且拟合精度明显优于前两者。

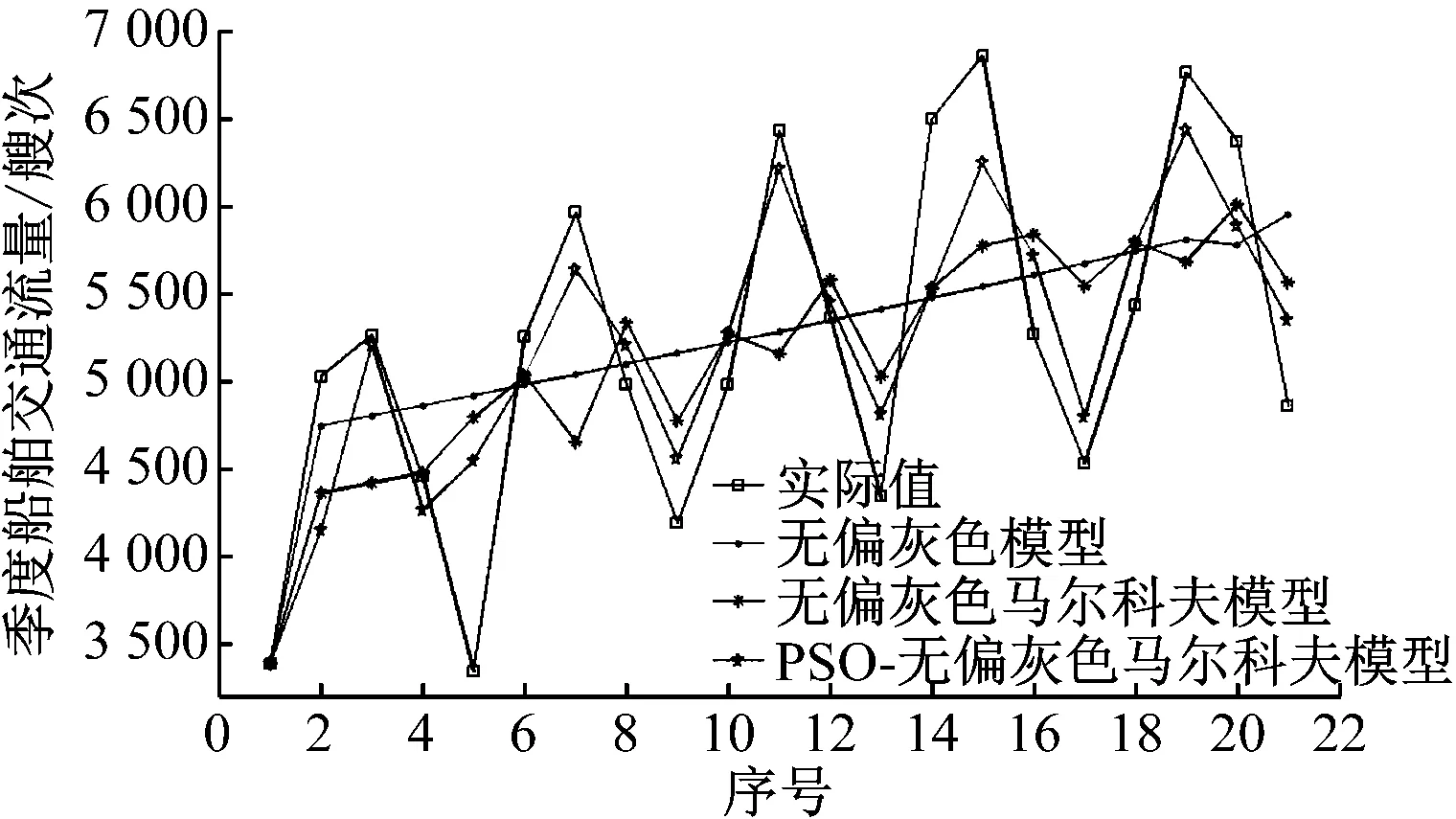
图2 船舶交通流量预测值结果对比

拟运用该方法对东营港2017年第2季度、2017年第3季度船舶交通流量进行预测。第21组数据转移到第22组、第23组数据的第1、第2步状态转移概率矩阵为

P(1)=P(0)×P(1)=0 1 0 0×P(1)

第21组数据处于E1，参照PSO-无偏灰色马尔科夫模型的计算过程和第2步状态转移矩阵，计算结果见表6。

2.5 误差比较

根据式(20)和式(21)，分别计算3种模型在对前21组数据进行拟合及对第22、第23组数据进行预测情况下的MAE和MAPE,见表7。

由表7可知:采用PSO-无偏灰色马尔可夫模型拟合误差中MAPE为8.561%，精度为91.439%，优于无偏灰色模型及无偏灰色马尔科夫模型，拟合较好。PSO-无偏灰色马尔可夫模型对于2017第2、第3季度的预测误差中MAPE为4.041%，精度为95.959%，验证模型的可靠性。

表7 3种模型误差比较结果统计表

3 结束语

1) 本文提出PSO-无偏灰色马尔科夫船舶交通流量预测模型,该模型在综合考虑预测中残差序列、状态区间和状态转移概率的基础上，自适应求解最佳白化系数，用以克服无偏灰色马尔科夫模型在预测波动性数据存在精度低的问题。

2) 本文模型与传统无偏灰色模型和无偏灰色马尔科夫模型相比，能确保更高精度的预测结果。

3) 为进一步提高船舶交通流量预测精度，后续工作将重点研究马尔科夫模型中的最佳状态划分方法和粒子群算法，有效克服船舶交通流量预测中的复杂性和非线性。

4) 预测结果可为港口水域的合理布局及海事主管部门提高水上交通管理效能提供基础性数据。