海上应急资源调度多目标模型优化

朱小林， 陈昌定

(上海海事大学 物流研究中心，上海 201306)

随着海洋经济的发展和海洋强国战略的推行，我国政府为贯彻落实《全国海洋经济发展“十三五”规划》，正在逐渐加强国家海上安全体系建设。据国家海洋局发布的《2016年中国海洋灾害公报》，2016年我国发生的各类海洋灾害共造成直接经济损失达50.00亿元，死亡/失踪60人[1]，海上突发重大事故造成的财产损失和人员伤亡十分严重。因此，从优化应急资源调度计划、综合考虑救援目标并提出合理的应急调度决策方面提高我国的海上搜救能力，对于降低海上灾害损失、促进海洋经济发展而言具有重要意义。

近年来，国内外相关学者[2-4]对应急突发事件的研究主要集中在应急物资分配、车辆路径优化和人员疏散等方面，广泛应用于地震、火灾和矿井塌陷等事故的应急处理中。已有的对海上突发事故的应急资源调度和优化问题的研究多集中在救助资源配备标准和应急船舶调度路径选择等方面。王军等[5]考虑水上事故救援的特殊性，对水上遇险目标漂移路径进行预测，求解满足运力、时间限制的应急物资需求模型。刘保占等[6]将海上应急救助分为2个阶段并引入救助资源包，针对救助点变化分布规律建立科学合理的资源调度方案。CAUNHYE等[7]将优化建模技术应用到海上灾难领域，指出研究空白和未来的研究方向。WAGNER等[8]以优化船舶供应与站点需求之间的匹配为目标建立整数规划模型，利用风险价值和优化思想规避船舶短缺风险。

上述研究大多考虑的是应急救援的时间和成本，很少将应急响应时间、物资调度和船舶组合优化等多个目标进行综合考虑并加以分析决策。本文提出将应急响应时间、船队运营成本和救援船舶工作量与应急物资调度之间的匹配程度作为海上应急资源调度计划决策的3个目标函数，建立海上事故发生区域分布模型和多目标混合整数规划模型进行优化求解。

1 问题描述

海上搜救是一项战略性决策，当海上灾难性事故发生时，需根据事故类型快速做出反应计划，提供相应的救援船舶和生活物资，提高人员的生存率和减少物质损失。发生不同类型的海上事故时需要特定类型的船舶实施救援，例如，发生火警事故时，海上救援部门必须指派一艘具有消防能力的船舶实施救援。因此，本文依据海上事故类型确定其严重程度并将其作为船舶调度标准，指派相应的救援船舶、按需提供救济物品；同时，合理规划救援船舶停靠位置，进一步明确海上救援船舶的责任区域。海上应急救援系统组织架构见图1。图1中：应急救援基地左侧船舶表示可停靠在其基地岸基上；责任区域内事件表示1 a内该区域可能发生的海上灾难事故；实线连接表示其岸基停靠的船舶能对责任区域发生某种类型事故做出应急响应计划；应急救援船舶需按照其类型分类停靠于对应的应急救援基地中。

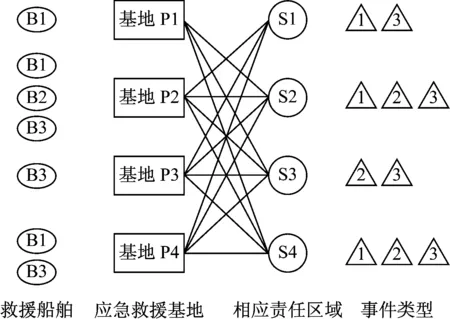
图1 海上应急救援系统组织架构

2 模型建立

模型建立步骤如下：

1) 根据海上事件类型的严重性，使用层次分析法(Analytic Hierarchy Process, AHP)对不同类型事件进行排序并分配相应权重。

2) 根据历史事件数据，建立区域分布模型并产生事故中心位置(模拟海上事故发生点)。

3) 建立多目标混合整数规划模型,以确定物资分配计划、救援船舶位置及基地责任区域。建模时应重点考虑：海上事故类型和事故点对物资的需求；船舶类型和应急物资种类(水、食物、船用救生衣和医药包)；地理因素；可用救援基地及其资源容量限制。

2.1 海上事故严重程度排序

根据事故中的救援难度、人员伤亡和经济损失等多项因子，按事件类型对海上事故的严重程度进行排序，是调度应急物资进行救助的根据，尤其是当物资量有限或稀缺时。本文参考已有研究AHP确定海上事件类型的严重程度。AHP是一种多方案/多目标的决策方法，已成功运用在海上应急资源调度研究中[9]。参考1-9标度法进行成对比较，该比例表示某个因素在较高级别因素上占主导地位的强度。比较值“1”表示比较项目同样重要；随着比较值的增大，重要性的差异越来越大；较大值表示比较项目具有更高的重要性。表示元素之间层次关系的结果决策树见图2。

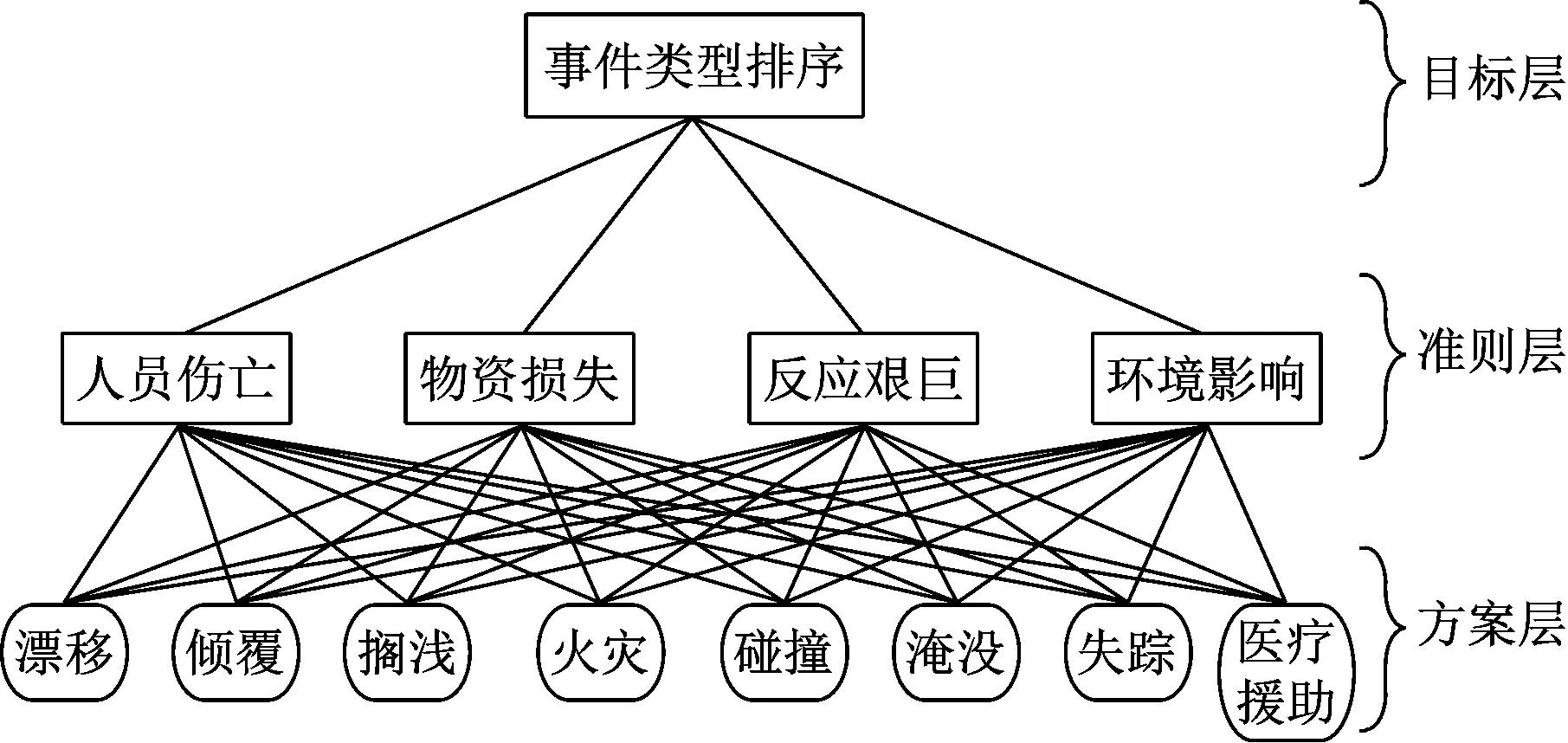
图2 表示元素之间层次关系的结果决策树

2.2 建立海上事故发生区域分布模型

同一海域某段时期内的海上事故发生点为离散型随机分布，若考虑所有事故发生点，将提高预先制定、及时调整应急资源调度计划的难度，影响其有效性。因此，采用创建聚合的方法对海上事故点的大规模数据集进行优化处理。FREDRIKSON等[10]将聚合定义为“用一个点代表一组数据点”，聚合能降低救援中心统计事故发生点的不确定性和难度，以便制订应急物资调度计划。由于不同事故点的严重程度(权重)有所不同，在采用聚类算法计算聚类中心时，必须考虑与每个事故点相关联的值。KERDPRASOP等[11]提出基于权重的k-均值聚类算法，即加权k-均值聚类算法，本文主要运用该方法划分海上事故发生区域。

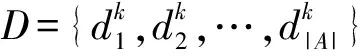
∀s∈S,i∈I,k∈K

(1)

2.3 建立多目标混合整数规划模型

基于各类型海上事故严重程度权重、事故发生区域划分及其物资需求量建立多目标混合整数规划模型，优化船舶和物资分配计划。相关集合、参数和决策变量定义见表1和表2。

本文以3个目标总和最小化为目标函数建立模型,其中：第一部分表示超出应急响应时间阈值的总加权偏差；第二部分表示超出船舶运作预算的加权偏差；第三部分表示与年度物资运输计划量相关的正负偏差之和总量，最大限度地降低正偏差和负偏差，达到平衡工作量的目标。模型方程式为

(2)

s.t

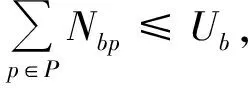
(3)

ybpub,min≤Nbp≤ybpub,max,∀b∈B,p∈P

(4)

(5)

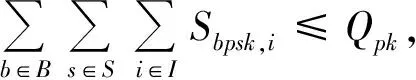
(6)

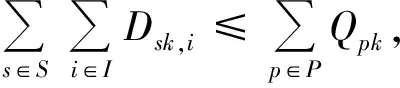
(7)

(8)

∀b∈B,p∈P,s∈S,k∈K,i∈I

(9)

(10)

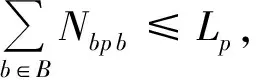
(11)

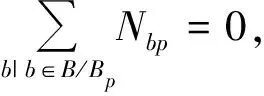
(12)

(13)

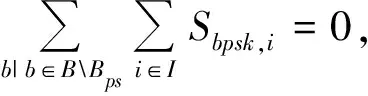
(14)

表2 决策变量定义

Rbpsλbpsi+Dbpsi,crt--Dbpsi,crt+=crti，

∀b∈B,p∈P,s∈S,i∈I

(15)

(16)

(17)

(18)

Nbp∈{0,1,2,…,n},∀b∈B,p∈P

(19)

ybp∈{0,1},∀b∈B,p∈P

(20)

λbpsi∈{0,1},∀b∈B,p∈P,s∈S,i∈I

(21)

式(3)表示被分配船舶数量不能超出实际拥有量；式(4)和式(5)分别表示应急救援基地p的各类型船舶分配量和物资存储量限制；式(6)表示各类型物资的供应量不超出基地实际存储量；式(7)表示各类型物资的总需求量不超过基地总存储量；式(8)表示物资供需平衡；式(9)表示总物资供应量的取值范围，M为无穷大正数；式(10)表示对应基地的船舶被充分使用；式(11)表示根据应急救援基地停靠的单种船舶长度来确定其停靠在基地的最大数量；式(12)表示相应基地的船舶停靠规则；式(13)表示各类型事故需要对应船舶输送相应物资；式(14)表示各类型船舶在其责任区域内响应事故；式(15)表示响应时间与临界响应时间阈值之间的关系；式(16)表示船舶分配量与预期物资计划量之间的关系；式(17)表示预算偏差；式(18)表示总的预期物资计划量正偏差不超过在相应基地船舶输送总物资的预期计划量。

采用GRODZEVICH等[12]提到的归一化技术，在量纲不同的多目标优化问题中缩放目标函数的加权和，在每个目标的解空间中计算2个特殊位置zg,U和zg,N，分别为最高点和最低点，即目标函数的上下限；利用这些点的差异给出归一化因子的计算式为θg=1/(zg,N-zg,U)，g∈{1,2,3}，其中ωg和θg分别为决策权重和归一化因子。

3 算例分析

鉴于海上事故相关资料的保密性和事故发生的复杂性和分散性，选择在渤海海域内仿真模拟8种事件类型、726个灾难事故点(时间为1 a)，确定各类型事故的严重程度权重、事故区域划分和物资需求数量，根据所建立的多目标混合整数规划模型进行求解；同时，定义一组反映船舶分配计划结果的性能指标，对几套船舶分配方案进行比较，进一步确定模型的量化影响。

3.1 试验结果

为方便计算食物救援生成药包等4种物资，同时对数量进行统一，单位换算见表3(水为10加仑/单位，食物为10包/位；其余均为1个/单位)。首先，运用AHP得到相关事故类型的严重程度权重和相应的物资需求量见表4，并据此绘制渤海海域灾难事故点分布见图3。

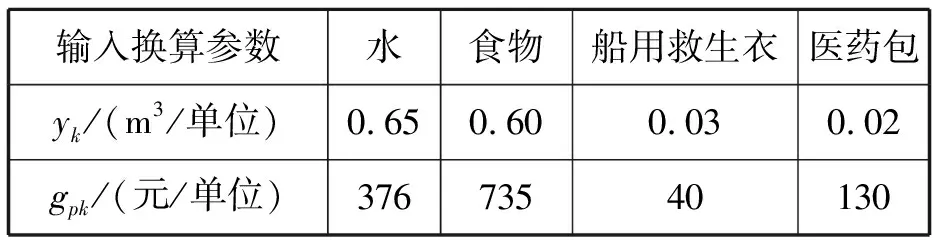
表3 单位换算

根据经验法则，聚类区域为|S|≈19个，运用加权k-均值聚类算法得到海上事故发生区域中心位置和该区域内的事故发生数分别见图4。根据北海救助局网站统计救援基地和船舶信息；以船舶运行速度、救援基地与责任区域之间的距离(利用海上船舶交通海洋距离计算器求取)来衡量应急响应时间。

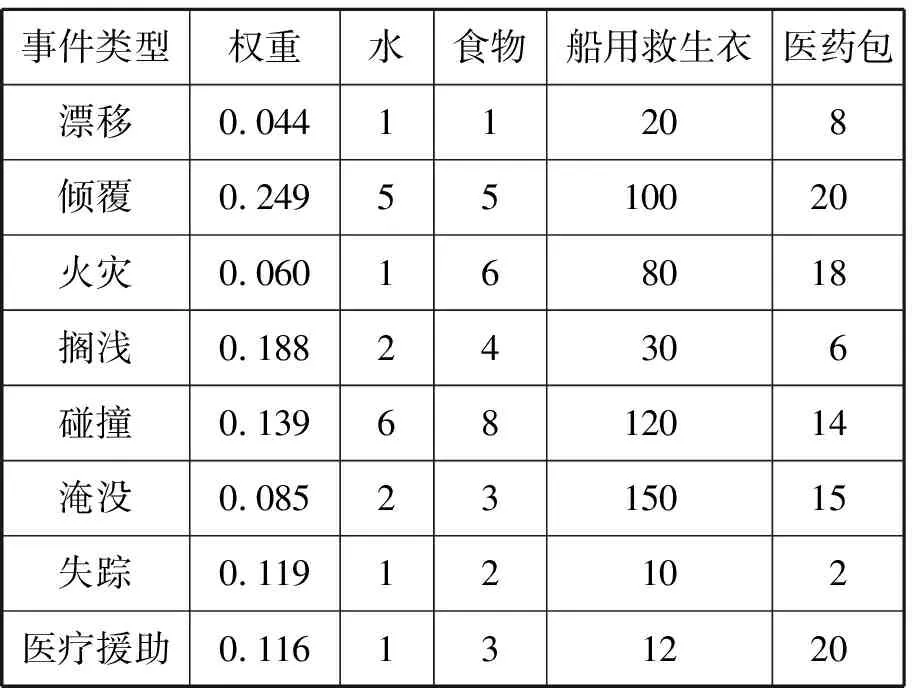
表4 相关事件类型主要参数

图3 渤海海域灾难事件分布图4 加权k-均值聚类算法求解结果

为验证多目标混合整数规划模型的有效性，制定8种性能指标(PM1～PM8)的计算式进行比较。考虑到海上应急救援应以及时性为首要目标，规定对目标函数中的延迟分量赋予较大权重，制定当ω1=0.5、ω2=0.25、ω3=0.25和ω1=0.9、ω2=0.05、ω3=0.05时的分配计划进行比较。表5为性能指标和模型分配结果，旨在突出应急救援总延迟最小，同时将预算和预期物资计划量权重保持在较低的水平。2种计划的PM3指标值均为0，说明在这2种计划下的海上应急救援计划不会发生预算短缺；从PM4指标的结果中可看出2种计划均节约预算(分别为17%和13%)，主要原因是与船队规模利用率相关的总年度固定救援运作成本下降，如PM8对应的78%(计划1)和88%(计划2)；PM5～PM8表明不同权重将导致船舶工作量与预期物资计划量之间的不匹配关系增加。由计划1和计划2的结果可知，针对目标函数不同分量权重变化的权衡结果，如计划1延长总延迟时间、更低的成本和缩小船舶工作量与预期物资计划量之间的不匹配关系，计划2与之相反。因此，依据多目标混合整数规划模型设定计划对海上应急资源调度有显著的积极影响。

表5 性能指标和模型分配结果

模型不考虑需求的变动性，同时模型中与需求变异性相关的风险已被纳入救援系统：

1) 任何实施的最佳计划，都将有与保持15%的船队规模相关的预期物资供应量安全库存。

2) 考虑到救援计划的长期规划，根据预测事件数量使用需求估算值，并利用步骤二中的区域分布模型更新数据。

3.2 灵敏度分析

为进一步阐述多目标混合整数规划模型的实施效果，按目标函数3个分量设置不同权重值进行灵敏度分析。不同权重下目标函数性能指标值见表6。由表6可知：赋予各项不同权重值时均无预算短缺风险；由目标函数分量ω1、ω2和ω3可知，测试案例1～4、6～15与目标函数3个分量权重一致的情况(案例5)相比，目标函数分量取值存在差异时性能指标随之发生变化，因此在实际中根据基地、船舶、事故情况时效性来设定ω1>ω2、ω3，分配目标函数分量权重，对于制订海上应急调度计划而言是有意义的。仅考虑应急响应时间下的案例15总延时时间降低到1.003 h，见图5，对于整个海上应急系统而言几乎可消除延迟，但消耗物资量和船舶工作量与其他案例相比有大幅提高，因此基于多目标模型制订调度计划具有协调作用。同时，由图5中的测试案例11可知，其船队规模利用率与预算使用占比相等(均为85%)，说明已协调船舶工作量与应急物资调度之间的不匹配关系，总权重延迟时间为3.421 h。

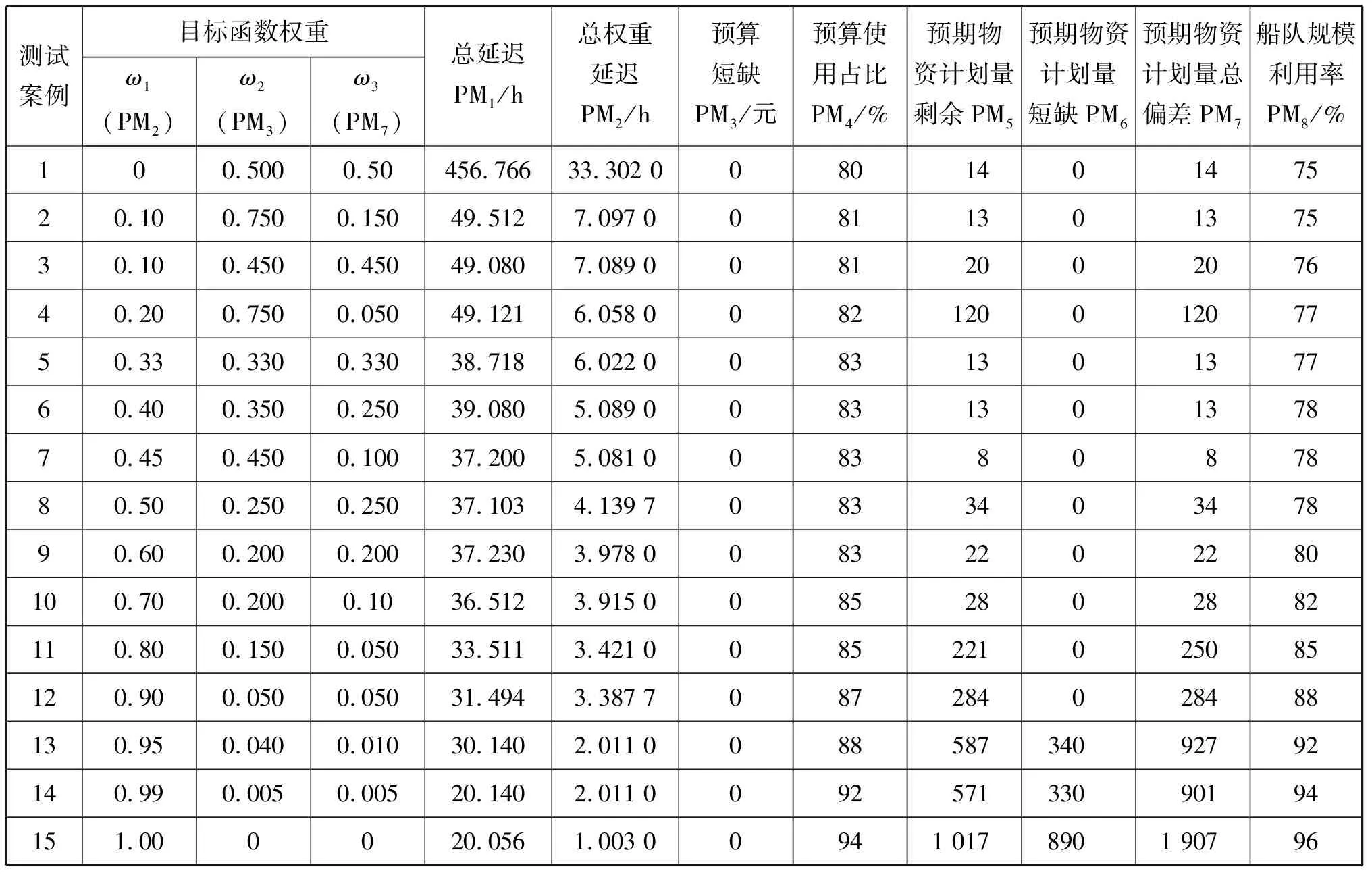
表6 不同权重下目标函数性能指标值

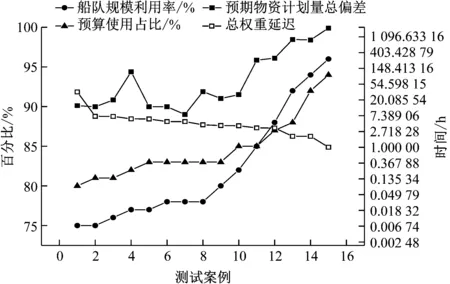
注：船队规模利用率和预算使用占比参数参考左边垂直坐标轴，其余的参考右边垂直坐标轴

图5 每个测试案例所对应的船队规模利用率、预算使用占比、预期物资计划量总偏差、总权重延迟的值

图5直观地展现了各测试案例的船队规模利用率(PM8)、预算使用占比(PM4)、预期物资计划量总偏差(PM7)和总权重延迟(PM2)之间的总体权衡。结果表明：由于船队规模利用率提高，应急响应时间大大降低；当响应时间缩短时，船队利用率和预期物资计划量总偏差都增大。在所有情形下，总运营成本均低于预算且总权重延迟时间在渐渐降低。最后，取第2组测试案例详细说明根据模型求解所得应急资源调度计划(见表7)、船舶分配计划(见表7)、救援基地的物资储存计划(见表8)。

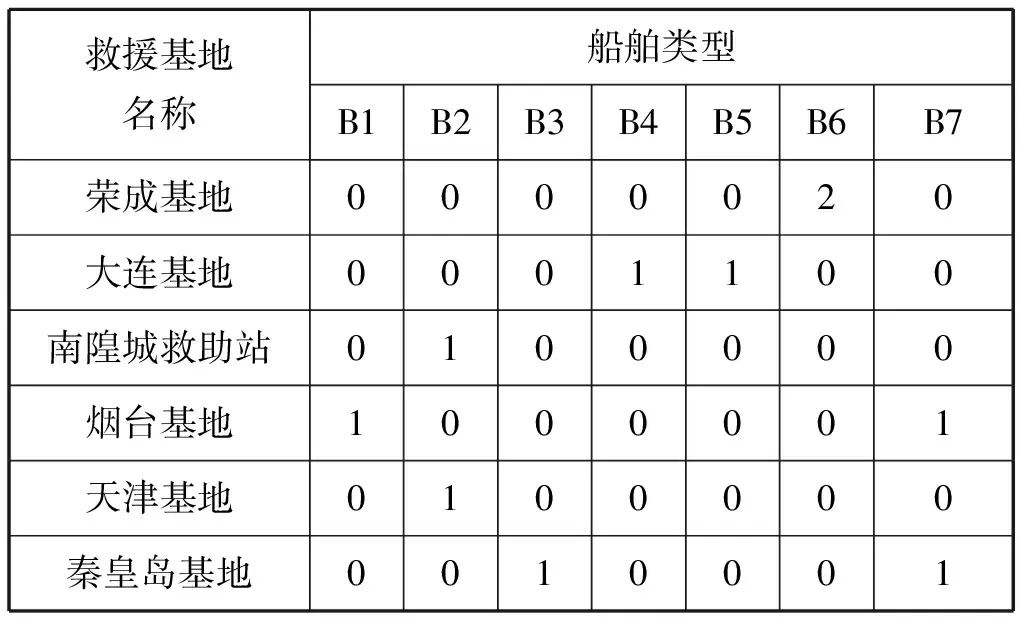
表7 测试案例2下船舶分配方案

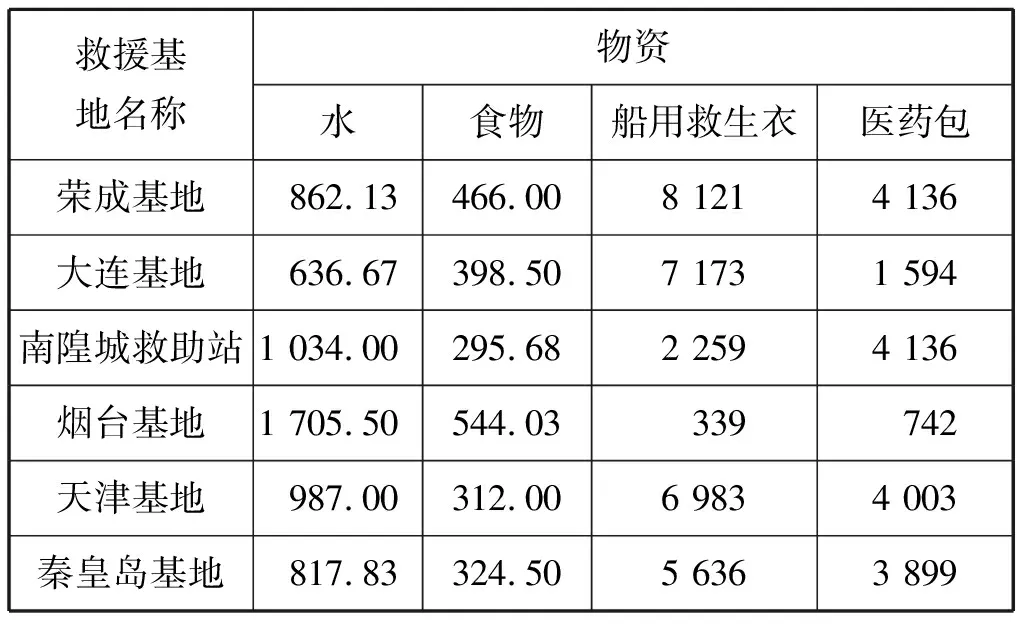
表8 测试案例2下物资分配方案

4 结束语

根据仿真案例分析，模型能很好地应用于渤海海域灾难事件救援方案中；通过列举目标函数分量在不同权重情况下的调度计划可知，模型具有一定的有效性。

本文定义不同权重下的2个计划，并根据目标函数对8个性能指标进行评估。结果表明，该模型对多目标海上应急调度计划有显著的影响，在以总延迟时间为首要目的的前提下，计划1的总权重延迟时间略高于计划2，但其在大大节约总体救援预算同时具有较佳的物资分配计划。此外，比较分析目标函数分量不同权重设置对整体分配计划的影响。结果表明，充分发挥船舶利用率可实现给定预算水平下应急事件响应时间缩短，这对实际运用中救援部门根据整体情况及时制订资源调度计划具有重要的借鉴意义。

未来可考虑海上事故偶发性，研究海上动态值班待命点处救援船舶的分配，并实施动态优化模型，包括在应急救援基地之间重新定位船舶和物资最佳分配计划。该方法可进一步提高模型的有效性，并可通过调整应急救援基地的停靠船舶数量来最小化应急响应时间。