基于Hamilton理论的船舶柴油发电机组控制策略

梁浩哲, 韩 冰, 张丹瑞

(上海船舶运输科学研究所 航运技术与国家安全重点实验室， 上海 200135)

船舶电站作为船舶航行中的主要供电设备，为全船照明用电负载和其他辅助装置提供连续稳定的电能。[1]随着船舶电力系统的发展，其结构也越来越复杂，在诸如负载突变、各副机的工况切换、支路发电机并网与反并网等情况下，船舶电站是否仍然能保证电能质量和系统的稳定性已受到业界越来越多的关注。

船舶电站主要由柴油机作为原动机拖动同轴同步发电机发电，系统中调速控制器作用于柴油发电机的调速系统，调节发电机输出电压的频率；励磁控制器作用于柴油发电机的励磁系统，调节发电机输出电压的幅值。现有的控制策略将这2种控制系统分开看待，每一种控制器的被控对象都是单一的，其实现方法多用传统的比例积分和微分(Proportion Integral Differential,PID)控制器闭环控制，但其鲁棒性欠佳。[2]

船舶电站系统是一种比较复杂的非线性控制系统，其中输出电压幅值和原动机转速是一对相互耦合的非线性变量，在大型负载突增突卸的情况下，这些扰动会对柴油发电机组产生明显的非线性参数扰动，增加模型的不确定性。[3]无论是使用常规的线性系统控制方法还是将非线性系统近似线性化处理的方法都难以达到满意的效果。因此，对于船舶电站系统在设计控制器时需考虑到负载扰动对系统的影响。[4]较为理想的控制策略是将调速控制器与励磁控制器两者有机结合起来，对系统进行协调控制，以此来改善船舶电力系统的暂态稳定性。

针对船舶电站这一能量耗散系统，先分析并构建柴油机组的非线性数学模型，用数学表达式清晰表示出非线性变量间的耦合关系；然后，基于Hamilton能量耗散理论设计Hamilton协调控制器；最后，通过MATLAB/SIMULINK平台搭建仿真模型，将Hamilton协调控制器应用于单机可变负载，支路柴油发电机并网等多种场合来验证该协调控制器在抑制扰动，提高系统暂态稳定性方面的优势。

1 船舶电站系统建模

船舶电站系统主要由发电装置(发电机)、配电设备(断路器、各种配电板等)、输电设备(各种线缆)及用电设备(通信设备、电动机、照明装置等)等4部分组成。[5]从控制系统的角度出发，传统的控制方法是对调速系统和励磁系统的被控对象分别控制，即采用2个单闭环控制系统，从发电机输出的电流变量经过坐标变换就可给各个静态负载和动态负载供电。船舶柴油发电机控制原理见图1。

图1 船舶柴油发电机控制原理

1.1 船舶柴油机组建模

以船用柴油同步发电机组为例，根据其各部分工作机理，可建立其非线性数学模型[6]为

(1)

1.2 柴油机组非线性模型的坐标变换

(2)

令ω0=1，U2=Efd，式(1)在坐标变换式(2)下变换为

(3)

2 基于Hamilton能量理论的控制器设计

若存在一个广义受控的Hamilton系统[7]，可以将其表示为

(4)

(5)

式(5)中:K为一个正定矩阵，使得如式(4)所表示的Hamilton系统在平衡点处渐进稳定。

(6)

可将式(3)表示为广义受控形式，即

(7)

式(7)中：

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

进而，可得到控制规律为

(16)

式(16)中:参数k1>0，k2>0，参数的大小可根据需求设计。将式(15)代入式(16)可得

(17)

再将式(17)代入式(3)，就可得到

(18)

式(18)就是带有Hamilton协调控制器的柴油机组模型。

3 仿真与分析

为验证Hamilton协调控制器的控制效果，基于MATLAB/SIMULINK中Sim Power Systems仿真平台建立具有Hamilton协调控制器的柴油机组模型。仿真参数明细见表1～表3。模型采用变步长，ode23tb算法进行仿真。在仿真过程中，采用的PID参数为：KP=20，KI=0.02，KD=5。

表1 系统参数

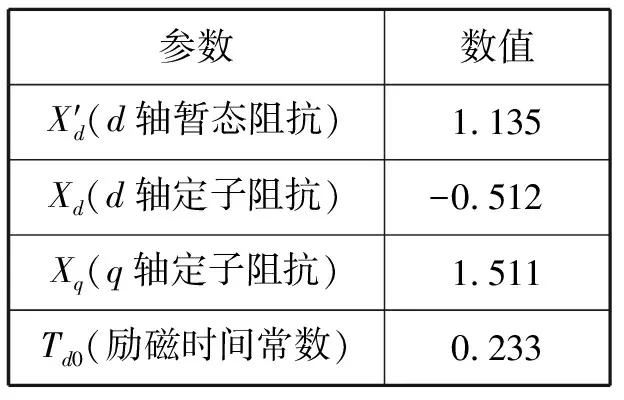
表2 发电机参数

3.1 空载启动特性对比

在空载状态下，同时启动由Hamilton协调控制器和PID控制器分别控制的2台柴油发电机组，SIMULINK仿真模型见图2，仿真结果见图3，对比数据汇总见表4。由图3可知:从0到建立起80%的转速，Hamilton协调控制器比PID控制器快0.3 s左右；从0到建立起80%的机端电压，Hamilton协调控制器比PID控制器快0.2 s左右，具有更好的启动性能，因而Hamilton控制器性能更佳。

表3 初始化参数

图2 空载启动特性对比仿真模型

a) 柴油机组空载启动转速变化曲线

b) 柴油机组空载启动励磁电压变化曲线

c) 柴油机组空载启动端电压变化曲线

时间Hamilton控制器PID控制器Tn80%1.01.3TV80%0.20.4

表4中:Tn80%为柴油发电机达到80%额定转速所需时间;TV80%为柴油发电机达到80%额定端电压所需时间。

3.2 静态负载突增突卸参数对比

在柴油发电机转速上升至额定转速后，分别在第5.0 s、第5.5 s、第6.0 s突增33.3%的静态阻感负载，并在第6.5 s突卸100%的静态负载，仿真结果见图4。

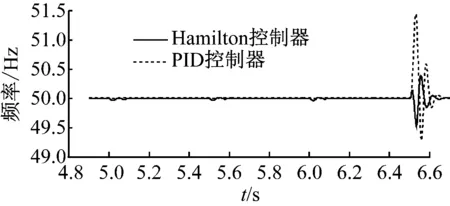
a) 静态负载突增突卸频率变化曲线

b) 静态负载突增突卸端电压变化曲线

c) 静态负载突增突卸母线电流变化曲线

从图4可知:在突增负载时，两种控制器均可以把发电频率和发电电压控制在较好范围内，而Hamilton控制器可较好地控制母线电流的波动性；突卸负载时，Hamilton控制器的最大超调量为1%，在PID控制器的最大超调量为3%。因此Hamilton控制器的控制效果较好，鲁棒性较强。

3.3 动态负载突增突卸参数对比

采用异步电动机模拟船用起重电机，对控制器控制动态负载的鲁棒性进行仿真测试，在第5.0 s、第5.5 s分别突增突卸动态负载，仿真结果见图5。从图5中可知：Hamilton控制器的频率最大超调量为0.24%，端电压最大超调量为0.45%；PID控制器的频率最大超调量为0.06%，端电压最大超调量为1%。

a) 动态负载突增突卸频率变化曲线

b) 动态负载突增突卸端电压变化曲线

c) 动态负载突增突卸母线电流变化曲线

3.4 并网与反并网过程参数对比

为测试两种控制器在并网与反并网过程中的鲁棒性，在Hamilton控制器和PID控制器分别控制的2台柴油发电机达到稳态后，分别并联运行状态安全相同的柴油发电机。在第5.0 s并网，在第5.5 s反并网，仿真结果见图6。由图6可知：Hamilton控制器的频率和端电压超调量几乎为零；PID控制器的频率最大超调量为0.8%，端电压瞬时超调约13%。因此Hamilton控制器的柴油发电机在并网反并网中的参数波动几乎可以忽略不计，具有很好的鲁棒性。

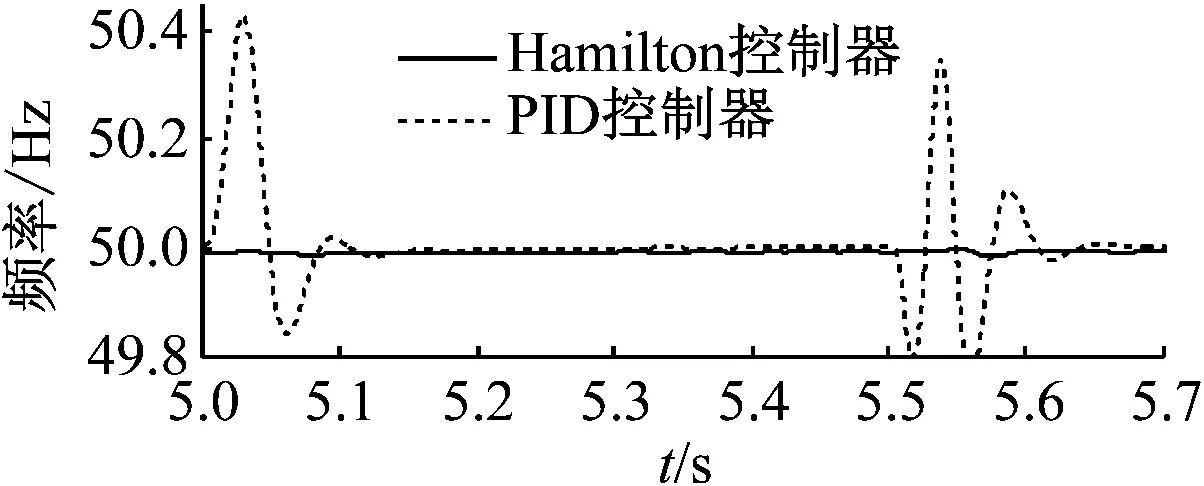
a) 并网与反并网过程频率变化曲线

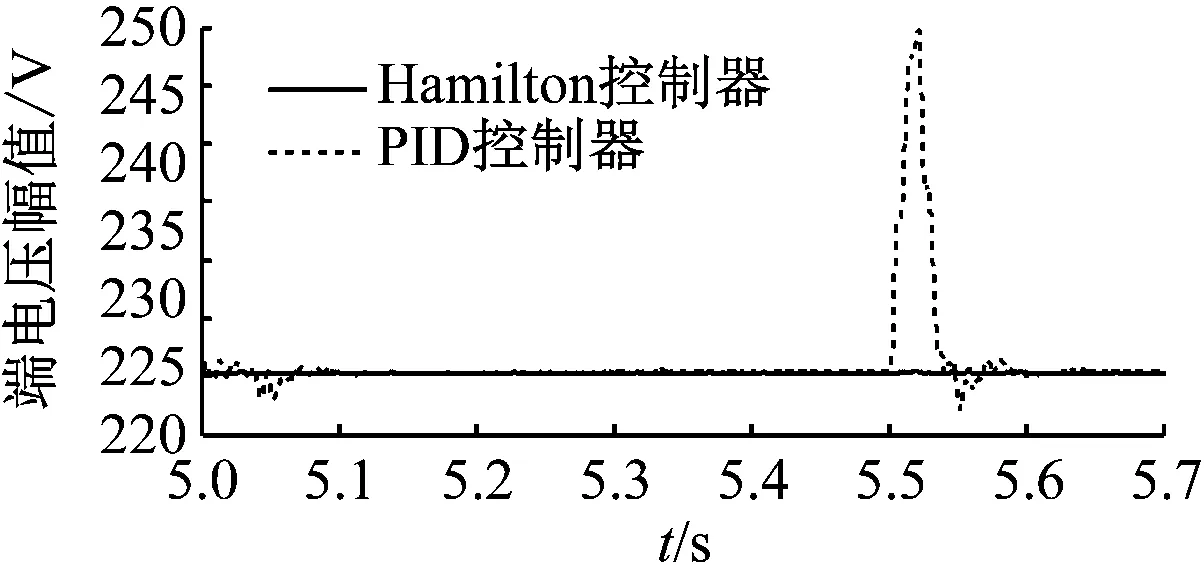
b) 并网与反并网过程端电压变化曲线

c) 并网与反并网过程母线电流变化曲线

两种控制器在不同仿真过程中的超调量对比见表5，其中：σf为频率最大超调量；σV为端电压最大超调量。

表5 两种控制器在不同仿真过程中的超调量对比 %

4 结束语

为验证Hamilton协调控制器在改善船舶电站系统的有效性，基于Hamilton能量理论建立和设计船舶柴油发电机的非线性数学模型及其调速励磁协调控制器。与传统的PID控制器对比，Hamilton控制器针对船舶电站非线性的控制系统，具有一定的优越性。仿真结果表明:采用Hamilton协调控制器的柴油发电机可减少船舶电站系统在负载突变、工况切换、并网发电等过程中的波动性，提高系统的稳定性。