非标准有限差分法求解薛定谔方程
2019-05-09刘明鼎张艳敏
刘明鼎, 林 鑫, 张艳敏
(青岛理工大学琴岛学院 基础部, 山东 青岛 266106)
薛定谔方程是物理领域量子力学的一个重要方程.可以用来讨论单色波的一维自调适、光学的自陷现象、固体中的热脉冲传播、等离子体中的Langnui 波、超导电子在电磁场中运动以及激光中原子的Bose-Einstein凝聚效应等[1-3],也被用于研究深水波浪理论、柱(球)非线性薛定谔方程[4-5],因此研究此类方程具有重要的意义.本文结合构造非标准有限差分格式的特点[6-8],给出求解薛定谔方程的一种非标准有限差分格式.通过分析,证明了构造的差分格式是无条件稳定和收敛的.数值算例验证了该方法是有效的.
1 两种非标准有限差分格式的构造
考虑如下初边值薛定谔方程:
初始条件
u(x,0)=φ(x),0≤x≤L,(2)
边界条件
u(0,t)=φ0(t),u(L,t)=φ1(t),0 这里i为虚数单位,f,φ,φ0,φ1为已知连续函数,L,T为非负常数. 利用MICKENS方法[6],以及文献[9-11]在网格点处对式(1)离散后的差分方程为 对式(5)进一步整理 则式(6)即为式(1)第一种非标准有限差分格式. 定义差分符号 其中,分母函数D1、D2与式(4)所对应的分母函数相同.对式(7)进行整理得 则式(8)即为式(1)第二种非标准有限差分格式. 利用标准的有限差分方法构造的显示有限差分格式为 考虑如下初边值问题: 表1 数值解误差Table 1 Error of numerical solution 续表1 (x,t)精确解实部虚部格式一误差实部虚部格式二误差实部虚部标准差分格式误差实部虚部(0.6,1.0)0.984491.533264.125×10-45.891×10-46.102×10-47.048×10-48.698×10-47.162×10-4(0.7,1.0)1.088041.694513.266×10-54.125×10-53.000×10-54.059×10-58.123×10-38.168×10-4(0.8,1.0)1.202461.872733.200×10-43.128×10-44.159×10-42.618×10-45.136×10-45.126×10-3(0.9,1.0)1.328932.069682.981×10-45.269×10-42.782×10-42.998×10-43.025×10-36.024×10-4 非标准有限差分格式的构造需要考虑偏微分方程解的特征.非标准格式在保持原偏微分方程的性质方面比传统的差分格式更有效[11-13].目前还没有研究薛定谔方程的精确差分格式的相关文献.在接下来的工作中,将利用文献[6-7]的方法讨论深水波浪非线性薛定谔方程的精确有限差分格式.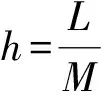
1.1 第一种非标准有限差分格式的构造


1.2 第一种非标准有限差分格式的局部截断误差
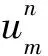



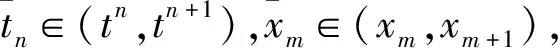
1.3 第二种非标准有限差分格式的构造

1.4 第二种非标准有限差分格式的局部截断误差




1.5 标准有限差分格式
2 数值算例
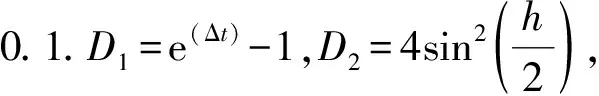


3 结 论
