时序IO与AO型异常值稳健联合检测法及其应用

王志坚，王斌会

（1.华南师范大学 经济与管理学院，广州 510631；2.广东财经大学 统计与数学学院，广州 510320；3.暨南大学 管理学院，广州 510632）

0 引言

金融时间序列数据在观测过程中经常会受到一些突发事件的影响，如金融海啸或新监管政策的颁布等，这些事件往往会导致异常点（也称离群值）产生。虽然关于时间序列异常点分类的标准并不统一，但从现有的文献看，加性异常点（AO）与革新异常点（IO）是最基本的分类形式。时间序列异常点往往携带重要的投资信息。因此，如何快速、有效地从金融时序中找到这些异常点并挖掘出其背后所隐含的投资信息，对于金融风险的研究不仅具有理论上的意义，而且具有较强的现实价值。

关于时间序列异常点检测方法的研究，在早期，学者们多是基于时间序列线性模型寻找离群值[1-4]。近年来，学者们开始关注非线性时间序列模型的异常值检测[5-8]。本文在参考文献[9，10]的基础上推导出了IO及AO型异常点稳健联合检测法。并通过模拟和实证分析验证了稳健联合检测法的可行性和有效性并将其应用于金融时间序列数据异常值的检测。该方法不仅对于金融风险的研究具有理论上的意义，而且对金融时间序列的稳健建模具有一定的参考价值。

1 时序IO与AO型异常点稳健联合检测法原理

对于时序IO型异常点检测原理文献[9]有详细的阐述，这里就不重复。由文献[9]可知，对IO型异常点的检测关键是要计算出检验统计量值，而λ取值由模IO型残差aT及标准差σ决定。显然，标准差σ是不稳健的，单个极端值就能将其改变很大，从而极大影响了IO型异常值的检测效力，因此有必要对σ进行稳健改进。

而对于时序AO型异常点检测原理文献[10]有详细的阐述，由文献[10]可知，对AO型异常点的检测关键是要计算出检验统计量值。显然λ由τ、ω、σ AoATa决定。由前文分析可知，τ取决于时间序列结构，而ωAT由τ及含有异常点模型残差ei所决定，但每个观测值模型残差ei只与观测值自己本身有关，各个观测值对彼此的残差互不影响，因而λAo的取值主要由τ及σa决定。τ及σa须由样本数据进行估计，而σa的估计与每个观测值息息相关，当样本数据存在异常点时，σa常被高估，甚至单个极端的异常点就能把σa变得面目全非，从而“淹没”（masking）或“掩盖”（swamping）现象发生，导致检测失败。因此为了准确计算检验统计量λAo，有必要对其进行稳健改进，也即对σa作稳健化变换。可见两种检测法的检测统计量均由于含有标准差而导致检验统计量不稳健。

另外，上文在介绍IO及AO型异常点检测原理时，有一个隐含的假设就是异常点类型是已知的，所不知的是异常点所发生时刻T。但在大数据时代背景下，由于各种随机因素的影响，使得实际的金融时间序列数据中通常含有多种类型异常点，即出现混合异常点现象，此时异常点类型和性质事先无从得知，需要将其检测出来。鉴于此，本文给出稳健联合检测统计量。

首先，要对两种异常点检测统计量的标准差进行稳健改进，标准差常用的稳健估计量有以下几个：

（1）缩尾标准差（WSD），表达式为：

缩尾标准差指的是缩尾数据的标准差。

（2）绝对离差均值（MAD），表达式为：

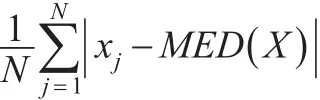
显然其稳健性体现在表达式中的中位数MED上。

（3）绝对离差中位数（MAD），表达式为：

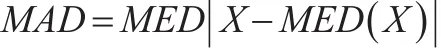
显然其稳健性体现在表达式中的双重中位数MED上。

（4）四分位数间距（IQR），表达为下：

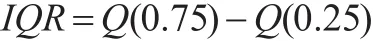
其中，Q(0.75)和Q(0.25)分别是数据由小到大排序后的第三和第一分位数。其稳健性体现在数据排序后异常点被排在序列的两端，当异常点比例未达到总数据的25%时，异常点对IQR没有干扰。

为避免异常点检测过程中发生“淹没”或“掩盖”现象，经反复试验比较，本文选用绝对离差均值来作为标准差σ的稳健尺度估计，即用去替代检验统计量和中的σ与σ，以达到抗异常值a目的，来提高检测效力。原始IO型异常点检测统计量经改进后变为如下稳健检测统计量：

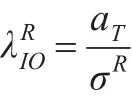
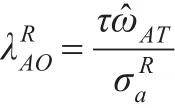
其中，表示稳健的表示稳健的σa。

其次，如在时刻T出现混合异常点现象，则只需先算出该时刻的稳健IO型异常点检测统计量及稳健AO型异常点检测统计量，再比较两种稳健检测统计量绝对值大小并作出判断：

具体检查流程图如图1所示：

另外，Jonathan D Cryer和Kung-Sik Chan（2008）提出用残差绝对均值乘以π作为标准差的稳健估计，本文将该方法记为J-K法，并比较原始检测法、J-K检测法及本文提出的稳健联合检测法的检测效果。

2 模拟研究

下面通过模拟来比较本文提出的稳健联合检测算法与传统检测法对异常点检测效力，在此用ARMA(1,1)模型模拟产生100个随机数，其中自相关系数为0.5，移动平均系数为-0.8。而后在该序列中随机抽取预先设定好的不同比例数据，用来自随机产生的均匀分布数据去替代之，作为ARMA(1,1)模型异常点。在此构造以下四种情形的污染率：ε=2%，ε=6%，ε=10%，ε=20%。需要说明的是，之所以将污染率比例设为偶数百分比，是因为在序列中需要构造IO与AO两种类型异常点，而且它们各占一半，个数均为整数。先给出四种被污染序列的时序图（如图2），以期从直观上了解被污染序列。

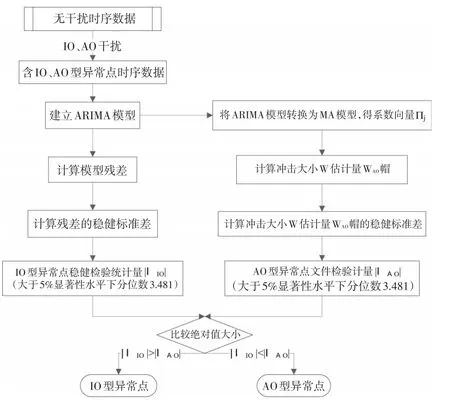
图1 时间序列IO与AO异常值稳健联合检测算法流程图

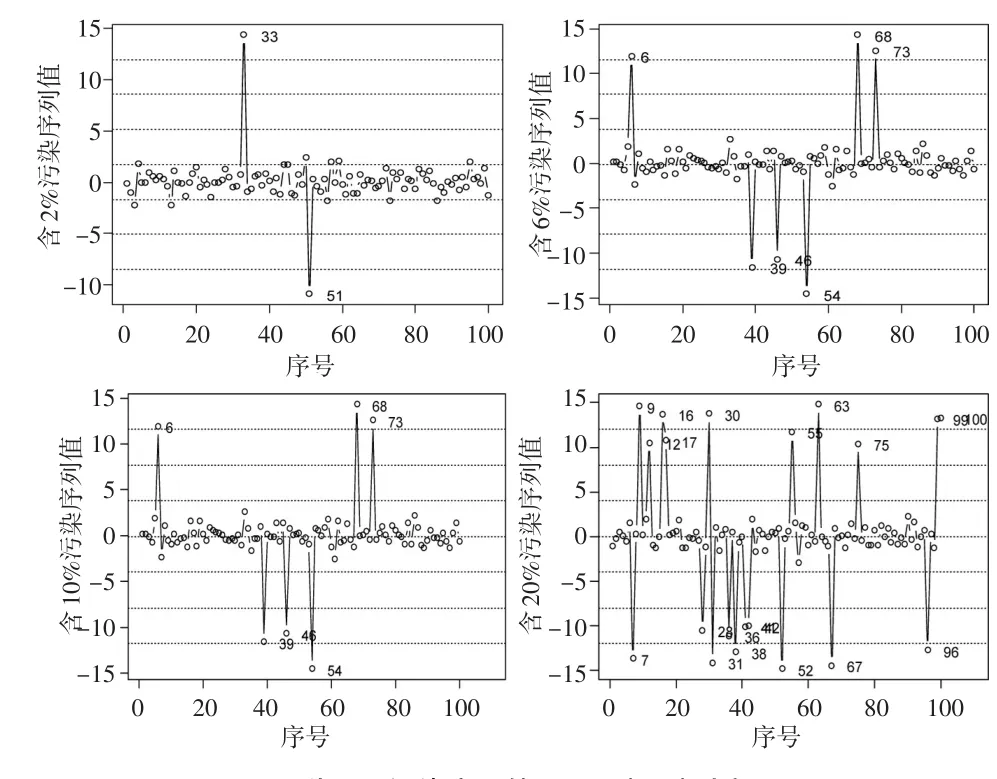
图2 四种不同污染率下的ARMA（1,1）时序图

接下来，分别采用原始检测法、J-K检测法及稳健联合检测法对以上不同污染率序列中的IO及AO型异常点进行检测，根据图1，用前面三种方法对以上四种污染率序列进行异常值检测，检测结果如表1及下页表2所示：

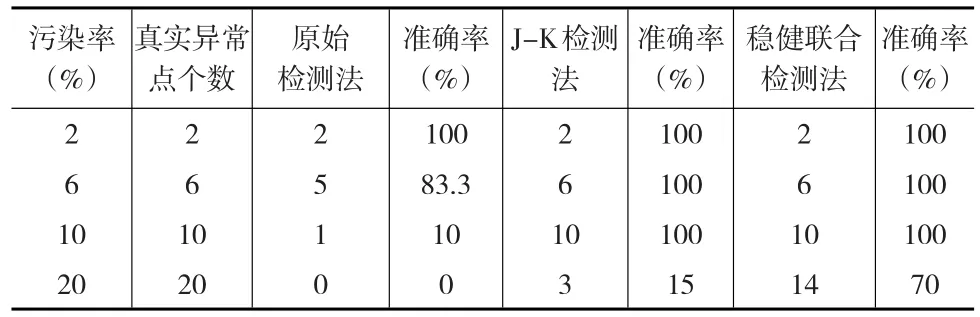
表1 三种检测法检测到总的异常点个数对比表

从表1可以看出，当污染率为2%时，稳健联合检测法与其他两种检测法一样，准确率为100%，说明稳健联合检测法具有可行性。而在后三种污染率情形下，本文提出的稳健检测法检测效力均显著高于其他检测法，说明稳健检测法具有有效性。

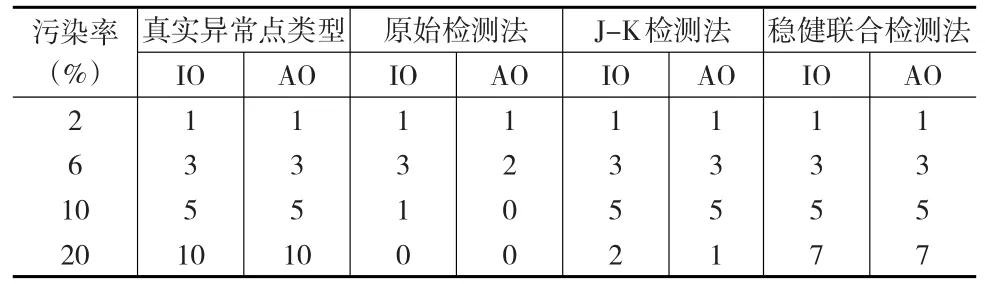
表2 三种检测法分别检测到IO及AO异常点个数对比表

从表2可以看出，以真实异常点类型个数为参照，当污染率为2%时，三种检测法均检测到IO及AO各一个,检测结果与真实个数一致。当污染率为6%时，原始检测法检测到3个IO异常点，2个AO异常点，而J-K检测法与稳健联合检测法均检测到3个IO、3个AO。可见，原始检测法漏检了一个AO，而后面两种检测结果与真实个数一致。当污染率为10%时，原始检测法只检测到1个IO异常点、0个AO异常点，而J-K检测法与稳健联合检测法均检测到5个IO、5个AO。可见，原始检测法漏检了4个IO、5个AO,而后面两种检测结果与真实个数一致。当污染率为20%时，原始检测法检测到IO、AO均为0个，而J-K检测法2个IO、1个AO，稳健检测法7个IO、7个AO。从总的检测结果来看，随着污染率的增加，三种检测法正确率均在减少，而原始检测法减少最厉害，特别是在高污染率情况下，显然原始检测法对异常点的检测已显得无能为力。其次是J-K检测法，稳健联合检测法正确率最高，虽有影响，但影响不大，可见稳健联合检测法改进效果显著。

3 实证检验

为了验证稳健联合检测的效果，本文选取深圳证券交易所的一只股票——贵州茅台，日期为2008年1月2日至2013年3月29日，共1267个样本，数据来源于锐思金融数据库(www.resset.cn)。选取贵州茅台这只股票是基于以下考虑：2012年12月中央出台了“八项规定”“六项禁令”及一系列限制公款消费的规定，在全国掀起了遏制公款消费的风暴，在这个背景下作为高端白酒中的“领头羊”、堪称“国酒”的茅台酒首当其冲受到影响，茅台股价及收益率理所当然离不开其销售量的影响，因此，此时研究该股票收益率的异常现象与本文的研究目标相吻合。

图3为贵州茅台收盘价及收益率图。可以看出贵州茅台的收盘价时序图的波动幅度还是比较大，其中分别存在一个明显的波谷及波峰；从收益率的时序图来看，图中有些值偏离主体数据较显著；因此初步判定茅台股票收益率数据存在异常值。

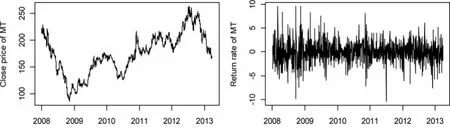
图3 贵州茅台收盘价图（左）及收益率图（右）

下面，按照稳健联合检测流程图对股票收益率异常点进行检测。首先建立时序ARMA模型，在建立ARMA模型之前需要确定模型的阶数，在这里用理论扩展的自相关函数表（EACF）来确定模型阶数，如表3所示，可以看出表3建议收益率序列拟合的模型为ARMA(0,0)。

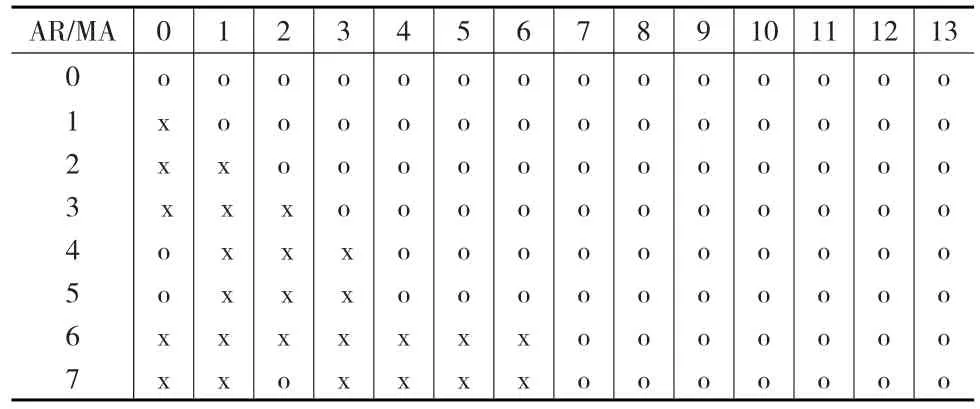
表3 收益率序列的EACF表

结合图3，可以判断导致这种现象的原因是收益率序列中有异常点存在，异常点干扰了序列的相关性。由于一般经济系统中在没有季节周期因素情况下，其自回归的阶数一般不超过5，移动平均阶数不超过2。为了拟合所需要的模型，下面对1至5的阶数组合后再进行反复试验，选取阶数的标准是：先看系数的显著性，再比较AIC的值，在这个标准下最后选择了模型ARMA(1,1)，估计结果如表4。

表4 序列{rt}的ARMA(1,1)模型参数估计结果

得到如下模型：

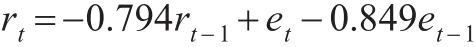
用该模型根据上文的检测原理，对异常点进行检测，表5为常规检测法检测到的异常点分布表。

表5 常规检测法检测到的异常点分布表

从表5可以看出，常规检测法共检测到9个异常点，其中AO型异常点4个、IO型异常点5个。表6为J-K检测法检测到的异常点分布表。

表6 J-K检测法检测到的异常点分布表

从表6可以看出，J-K检测法共检测到12个异常点，其中AO型异常点5个、IO型异常点7个。表7（见下页）为稳健联合检测法检测到的异常点分布表。

从表7可以看出，稳健联合检测法共检测到28个异常点，其中AO型异常点6个、IO型异常点22个。在所有被检测到的异常点中IO型居多，而且表中有2个年头异常点相对比较集中，分别是2008年与2012年。究其原因，2008年是因为汶川地震及全球金融风暴；2012年是受中央限制“三公消费”政策影响。这是原因都导致了贵州茅台这只股票的股价震荡不定，容易产生异常点。据了解，“三公消费”几乎占到茅台销售量的四成，中央“禁令”的出台导致2013年1月至4月茅台销售量下降23.8%。比较原始检测法、J-K检测法及稳健联合检测法对收益率异常点的检测结果，发现凡是原始检测法、J-K检测法检测到的异常点均被稳健联合检测法检测到，由此说明改进后检测法的可行性；另外发现凡是被稳健联合检测法检测到而未被原始检测法及J-K检测法检测到的异常点都是由于现实客观原因所导致。

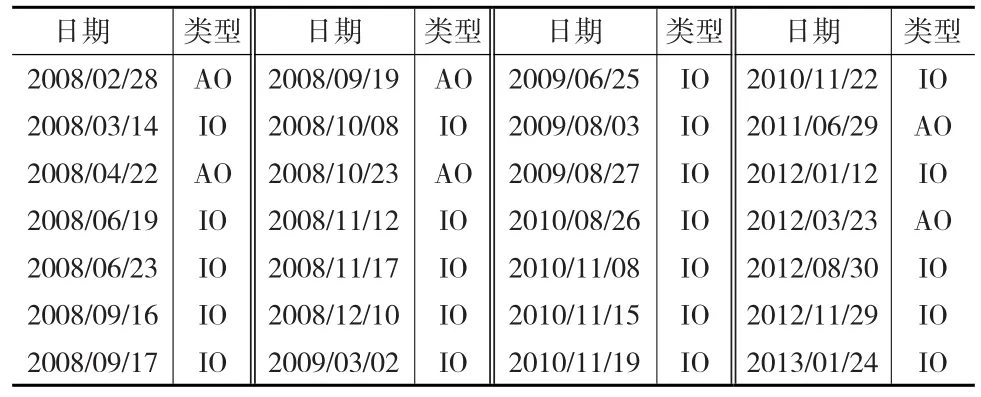
表7 稳健联合检测法检测到的异常点分布表

4 结束语

基于假设检验的IO、AO型异常点检测法检验统计量对离群值是敏感的，导致检验统计量不稳健。鉴于此，本文经反复试验比较，选用绝对离差均值作为标准差σ的稳健尺度估计，构建出IO、AO型异常点稳健联合检测算法。

模拟和实证研究均表明本文提出的稳健联合检测算法具有可行性和有效性，并且能更好地捕捉到我国金融市场的异常特点。该方法不仅对于金融风险的研究具有理论上的意义，而且对金融时间序列的稳健建模具有一定的参考价值。