部分线性变系数测量误差模型的随机约束估计

李 腾，苏宇楠，魏传华

（中央民族大学 理学院，北京 100081）

0 引言

考虑如下的部分线性变系数测量误差模型：

其中,Y为因变量,Z、X和U为自变量，β=(β1，β2，…βp)T为未知待估参数，α(·)=(α1(·)，α2(·)，…αq(·))T为未知非参数函数系数。ε是均值为零的模型误差，测量误差ξ与(Y，X，Z，U)独立，满足Eξ=0，Cov(ξ)=Σξ.,其中 Σξ已知。

对于模型（1），参数分量β的估计和检验一直是研究的重点。You和Chen（2006）[1]提出了校正profile最小二乘估计，并给出了所提估计量的渐近性质。实际数据分析中，除了样本数据本身，有时还能从其他途径得到额外信息，这些信息的加入能够提高估计的效率。这些额外信息的常见表现形式有两种：精确的线性约束条件和随机约束条件。对于经典线性回归模型，在含有精确线性约束条件时，考虑了约束条件的约束最小二乘估计优于没有考虑约束条件的普通最小二乘估计。当模型系数含有随机约束时，Durbin（1953）[2],Theil和 Goldberger（1961）[3]以及 Theil（1963）[4]将样本数据信息和附加的随机约束条件联合起来，提出了混合估计方法。关于线性回归模型约束估计的详细讨论可参考 Toutenburg（1982）[5]和 Rao等（2008）[6]。近年来，关于各类复杂模型的约束估计得到了关注。Shalabh 等（2010）[7]以及Li和Yang（2013）[8]讨论了线性测量误差模型的随机约束问题。对于模型（1）,Wei（2012）[9]讨论了当参数分量附加有精确的线性约束条件时的估计和检验问题。本文将研究模型（1）的随机约束估计,考虑如下的随机约束条件：

其中矩阵A为k×p行满秩，η为均值为0，协方差矩阵为σ2Ω的随机向量,其中 Ω为一已知正定矩阵,b是k×1的已知向量,针对模型（1）和模型（2），下文将重点研究未知参数分量β的估计问题。

1 参数分量的估计及其性质

首先假设自变量X可以精确观测，令为来自模型（1）的样本数据，从而有：

假设β已知，则模型（3）可记为：

显然,模型（4）是一个标准的变系数模型，下面采用局部线性方法对该模型进行估计。假设{ }αj(·)，j=1，2，…q二阶连续可导，对于u0附近的点u，由Taylor展开可得：

令：

其中Iq和0q分别为q维单位阵和元素全为零的矩阵。用α(Ui)代替模型（3）中α(Ui)，经过简单计算可得：

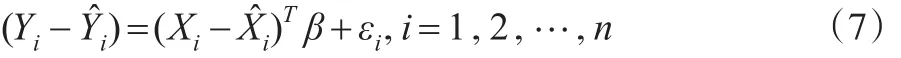
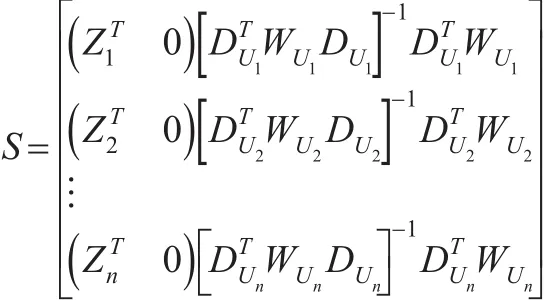
利用Theil和Goldberger(1961)[3]的方法,将样本数据信息和随机约束条件结合起来构造如下关于未知参数β的函数：

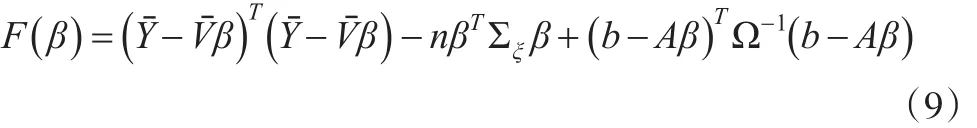
将F(β)关于β求偏导,并令其等于零，得：

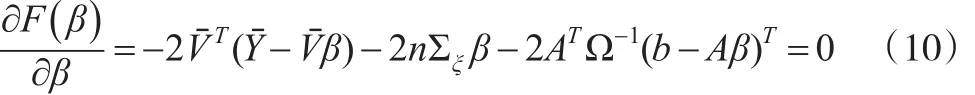
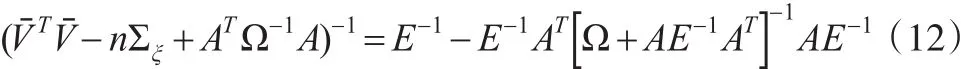
从而，由式（11）和式（12），可写为如下形式：

其中为式（8）中β的校正profile最小二乘估计。

下面给出所提估计量的渐近性质。定义表示AAT,

以及

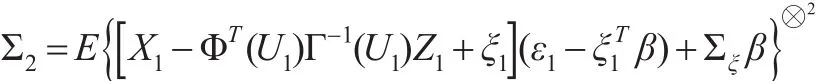
定理1：若假设A1—A6成立，

首先，给出证明定理所需要的一些假设，这些条件You和Chen（2006）[1]也采用过。

（A1）随机变量U具有有界支撑Π,其密度函数f(·)在其支撑上满足Lipschitz连续,且不为0。

从界面设计的角度上来说，信息传播是建立在人与人之间的一种社会活动，作为信息发布者和传播媒介的参与者，就需要融入群体中，了解历史文化景区形象传播活动的目的性和创造性，其中，目的性是指人类意识受信息传播控制的一种行为，具有较为明确的目标和对象作为规划的主题，在信息传播的全过程中具备一定的动机和方向。比如通过媒介广告对旅游景区艺术形象进行传播，经过策划获取宣传效果。在信息化视域下的旅游景区需要利用科学技术的传播方式，用最简单的语言和文字进行传播，在彼此的影响和相互作用下完成整个形象的信息传递[3]。

（A2）对于任一U∈Ω,矩阵E(zzT|U)为非奇异,E(zzT|U)，E(zzT|U)-1和E(zxT|U)都是Lipschitz连续的。

（A3）存在s＞2 使得E‖x‖2s＜∞ 和E‖z‖2s＜∞,对于ε＜2-s-1使得n2ε-1h→∞

（A4）{αj(·)，j=1，…，q} 二阶连续可导。

（A5）函数K(·)为对称密度函数，具有紧支撑。

（A6）nh8→0和

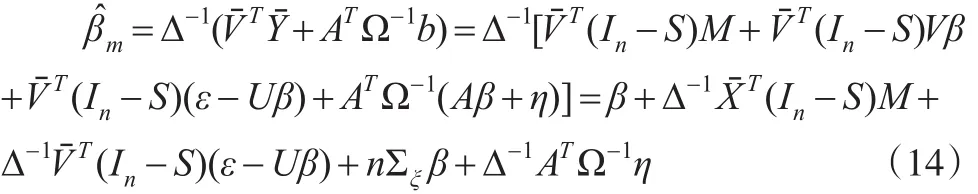
由 You和Chen（2006）[1]中的引理 A3 和 A4，可得：

再由式（19）和式（20），利用Slutsky定理，可得：

该结论表明校正profile混合估计的渐近性质与profile最小二乘估计的相同，这个结论在Shalabh等（2010）[7]以及Li和Yang（2013）[8]关于线性测量误差模型的讨论中也得到过。值得注意的是，虽然二者的渐近性质相同，但校正profile混合估计利用了附加的随机约束条件，二者在有限样本情况下的表现应该有所不同，下文将通过数值模拟来考察。

2 数值模拟

下面通过数值模拟来考察所提估计方法的有效性。假设数据来自于如下部分线性变系数测量误差模型：

其 中x1i～N(0，1)，x2i～N(1，2)，x3i～U(-2，2)，x4i～U(-1，1)，zi～N(1，1)，ui～U(0，1)，α(ui)=sin(2πui)， 测 量误 差

为了考察误差分布对估计结果的影响，将误差设定为如下三种分布形式，都满足均值为零，方差为1，(1)εi～N。核函数为K(x)为了计算方便，窗宽设定为h=n-1/5。参数分量 (β1，β2，β3，β4)=(2，1，3，3),样本量n=80,120,150,随机约束设定为β1+β2=3+η1和β3-β4=η2,其中Eη1=Eη2， 从 而有：

对于上述每次设定，重复500次，每次求出β的校正profile最小二乘估计和校正profile混合估计。这两类估计将基于估计的均方误差(estimated mean squared error,EMSE)这一指标来进行比较。EMSE定义如下：

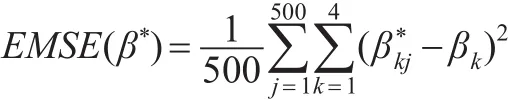
表1 两类估计的EMSE值比较

从模拟结果不难看出，随着样本量的增加，两类估计的EMSE都在变小。对于每种设定,βm的EMSE都要小于β的对应值，即在 EMSE 标准下,βm要优于β。

3 结束语

近年来，部分线性变系数模型的估计问题已经得到了广泛的研究，本文主要研究了该模型在线性部分自变量不能精确观测且参数分量附加有随机约束条件时的估计问题。给出了所提估计的渐近性质，并且通过数值模拟验证了所提方法的有效性。