基于线性规划和带重节点三次样条的Lorenz曲线逼近方法

2019-05-05梁学章

统计与决策 2019年7期

梁英,杨含,李强,梁学章

（吉林大学a.商学院；b.数学学院，长春 130012）

0 引言

Lorenz曲线是分析居民收入分布状况及财富分配不平等程度的重要工具，并且基尼系数的精确估计依赖于Lorenz曲线的精确估计。在已知居民收入分组数据的基础上,有多种方法逼近Lorenz曲线，如插值法、Lorenz曲线模型法等[1-3]。这些方法各有优缺点，但目前对中国分组数据的应用结果并不十分理想。本文针对《中国统计年鉴》已发布关于城镇和农村居民收入2006—2012年的分组数据,基于线性规划和带重节点三次样条提出了一种新的Lorenz曲线逼近方法，并应用这种方法估计了2006—2012年城镇和农村Lorenz曲线。该方法不仅精确插值所给分组数据,而且使得到的Lorenz曲线在保持凸性[4]的基础上具有更好的逼近性能。进一步,本文利用文献[5]所提供的方法进行加总,估计了相应的全国居民收入的Lorenz曲线与基尼系数，所估计得到的基尼系数值与国家公布的基尼系数十分接近。

将收集到的全国居民收入分配数据，以低收入端人口累计比例为横坐标，以该组人口拥有的收入占全国总收入的比例为纵坐标，在座标平面中绘点，再将这些点联接起来就得到近似的Lorenz曲线。通常认为Lorenz曲线是定义在[0,1]区间上的渐升的下凸连续曲线，满足L(0)=0,L(1)=1。将居民收入的分布函数、密度函数、分布函数逆函数分别表示为：

其中x∈[0，∞)为收入，p∈[0,1]为累计人口份额。平均收入记为：

则Lorenz曲线及其导函数可分别表示为：

显然有:

基尼系数是反映收入差距的指标，定义为Lorenz曲线与完全平均线之间面积的两倍，即：

1 带重节点三次样条保凸逼近方法的描述

设给定一组节点0=x0＜x1＜…＜xn=1,若分段函数s(x)满足如下两个条件:

（1）在每个区间[xj，xj+1](j=0,1,…,n-1)上,s(x)是一个次数不超过3的实系数代数多项式。

（2）s(x)在［0，1］上具有一阶的连续微商，则称s(x)为区间[0,1]上带有重节点的三次样条。

设由居民收入分组数据给出的Lorenz曲线L(p)的自变量值及其相应函数值分别为：

其中0=X1≤X2≤…≤Xm=1,0=Y1≤Y2≤…≤Ym=1,满足Yi=L(Xi)(i=1，2，…，m)。本文试图用[0,1]上带重节点三次样条函数s(p)逼近Lorenz曲线L(p),其中是的子集,并假定...,m)。

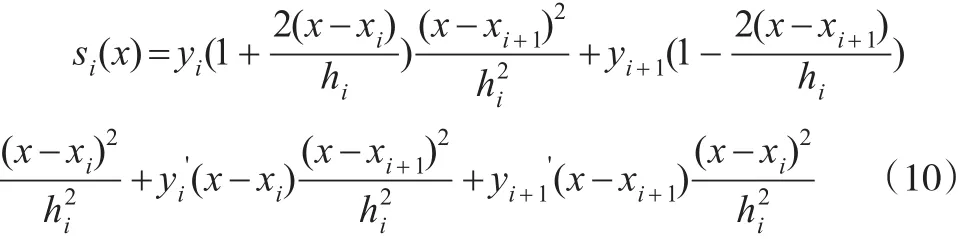
其中hi=xi+1-xi(0≤i≤n-1)

其二阶导数可表示为:

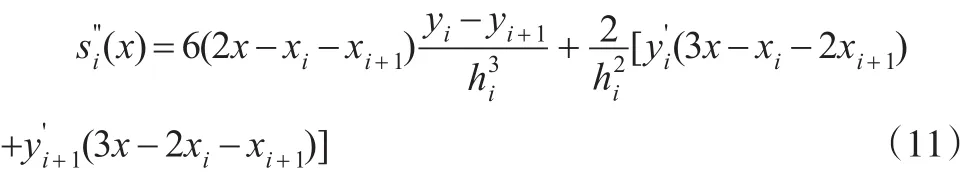
因此,s(x)在[0,1]上是单调上升的光滑凸曲线的充要条件为:

此时对应于s(p)的基尼系数可计算如下：

其中：

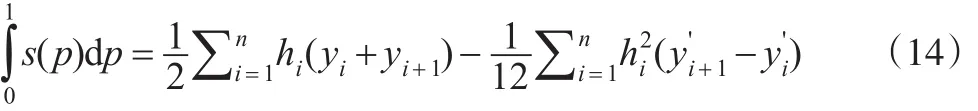
显然,满足条件（12）及条件s(Xi)=Yi,i=1，2，...，m的曲线s(x)均是逼近分组数据的Lorenz曲线。当式（14）中定积分达到极小值时,基尼系数达到极大值;式（14）中定积分达到极大值时,基尼系数达到极小值。

鉴于文献[1]和[5]根据中国统计年鉴所给的中国居民收入分组数据（此分组数据点数偏少）所推出Lorenz拟合曲线的基尼系数值偏小，为了使Lorenz曲线的逼近效果更好，本文采取了人为增加分组数据点的策略，即用带重节点三次样条来保凸逼近Lorenz曲线,并使得利用拟合的Lorenz曲线所算出的基尼系数达到最大值。从而将带重节点三次样条保凸逼近Lorenz曲线的问题转化为求解如下线性规划问题:

满足约束条件：

本文在逼近中国城镇和农村2006—2012年居民收入的Lorenz曲线时利用单纯形(大M)法[7]求解使得利用拟合曲线计算出的相应基尼系数达到最大值的线性规划问题,可分别计算出2006—2012年中国城镇和农村居民收入的Lorenz曲线及相应基尼系数。

下面分别介绍用带重节点三次样条保凸逼近中国城镇和农村的Lorenz曲线时引入样条节点的方式。设已给的城镇居民收入分组数据有m1组,引入样条节点后,城镇的样条节点可写为：

其中hi=xi+1-xi(0≤i≤n-1)。则逼近城镇Lorenz曲线的样条节点个数为n=3k+m1（在本文计算实例中m1=9,k=4）。

设已给的农村居民收入分组数据有m2组,引入样条节点后,农村的样条节点可表示为：

则逼近农村Lorenz曲线的样条节点个数为n=(m2-1)k+1(在本文计算实例中m2=5,k=4)。

2 加总Lorenz曲线的构造过程

设城镇总人口和乡村总人口分别为P1,P2，则全国总人口为P=P1+P2,全国城镇和农村的人口份额分别表示为，则

设城镇的收入分布函数、密度函数及Lorenz曲线分别表示为:

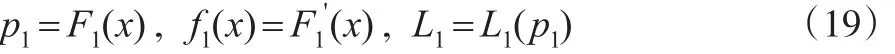
农村的收入分布函数、密度函数和Lorenz曲线分别表示为:

初始条件设为有机溶剂用量10mL，KOH甲醇质量浓度为0.2g/mL，用量5mL，提取温度为40℃，提取时间为2h，BHT添加量为0.2g，研究甲醇、四氢呋喃、正己烷和乙酸乙酯对稻谷中叶黄素提取效果的影响。取上述实验的最佳有机溶剂，溶剂用量分别设为 5mL、10mL、15mL、20mL，探究有机溶剂用量对稻谷中叶黄素提取量的影响。

又设全国Lorenz曲线为:

则加总后的Lorenz曲线计算公式[6]如下:

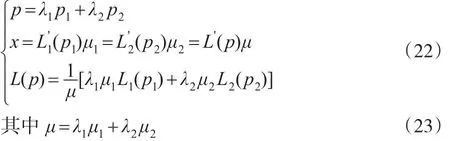
μ1、μ2分别是城镇和农村居民人均收入。

则由上述带重节点的三次样条保凸逼近方法得到的城镇和农村的Lorenz曲线及样条节点处的一阶导数值，利用加总公式（22），可导出加总的全国Lorenz曲线（具体加总方法见文献[5]）。

3 应用

本文将此方法应用于《中国统计年鉴》2007—2013年发布的2006—2012年关于城镇和农村居民收入的分组数据,分别得到了相应的Lorenz曲线和Gini系数逼近,并通过加总公式得到了全国居民收入的Lorenz曲线逼近。

（1）由《中国统计年鉴》2006—2012年中国城镇居民收入分组数据基于线性规划和用带重节点三次样条逼近所得到的2006—2012年城镇Lorenz曲线的函数值，如表1所示：

表1 2006—2012年城镇Lorenz曲线的函数值的估计

表2 2006—2012年中国农村Lorenz曲线的函数值的估计

（3）利用加总公式所得到的2006—2012年全国Lorenz曲线如下页表3所示：

表4（见下页）为2006—2012年我国城镇、农村居民收入的Lorenz曲线逼近的基尼系数。特别地，本文给出了中国2011年和2012年加总Lorenz曲线逼近的示意图（见下页图1和图2）。

4 结论

本文计算出的2006—2012年中国加总Lorenz曲线的基尼系数均高于林平关于2007年、Chen等关于2009—2012年的计算结果[8，9]（见表5）,低于国家统计局公布的2004—2006年度全国居民收入基尼系数（见表6），但非常接近。这说明上文所提出的目标函数极小化从而使得基尼系数最大化的策略是适宜的，本文提出的用带重节点三次样条保凸逼近的方法不仅保持了Lorenz曲线的单调性和凸性，还具有更好的逼近性能。可见，根据《中国统计年鉴》公布的分组数据计算出的加总Lorenz曲线的函数值是有一定参考价值的。