莱斯信道下大规模MIMO波束成形方法研究*
2019-04-30刘皖宁廖程建李姗鸿陈毓锴
刘皖宁,廖程建,李姗鸿,陈毓锴,许 魁
(陆军工程大学 通信工程学院,江苏 南京 210007)
0 引 言
在大规模多输入多输出(Massive Multiple-input Multiple-output,Massive MIMO)系统中,基站配备了多根天线,有几十根甚至几百根,较4G系统中的4(或8)根天线数增加了一个量级以上,这些天线以大规模阵列方式集中放置,以相同的频率服务于多个单天线用户。众多学者研究表明,基站配备的天线数越多,用户间信道的正交性越强,不仅提高传输利用率和无线系统容量,还增加了链路的可靠性,并减小了系统干扰。由于该系统突出的优点,大规模MIMO技术也被列为5G的关键技术之一。
目前,高速铁路已成为人们生活中重要且不可缺少的一部分。我国80%以上高速铁路都建在高架桥上,而高速铁路最典型场景就是高架桥。由于高架桥高度增加了用户天线的高度,所以信号在传输时,必然存在直射波。因此,在直视路径(Lineof-Sight,LOS)存在条件下,大规模MIMO信道将成为典型莱斯信道。然而,许多现有开创性工作简单地假定了瑞利信道衰落条件,当信道存在LOS分量时,瑞利信道已经不能准确刻画信道衰落变化,这时莱斯信道衰落模型能更好地描述此类信道。
在大规模MIMO系统中,目前广泛应用的是基于阵列结构的物理信道模型,例如空间信道模型[1]。相较于传统的基于全维大规模MIMO信道的信道估计与波束成形方法,本文提出一种基于空间基扩展模型的信道估计与波束成形方法。通过引入旋转角,从而将多用户大规模MIMO信道分解为多个并行的单用户通道,消除用户间干扰,提高系统的频谱效率。本文第二部分描述系统模型,第三部分介绍旋转角算法,第四部分对模型进行信道估计,第五部分提出优化用户分组算法及波束成形方法,第六部分给出仿真结果。
符号表示:(·)T,(·)H,(·)*,(·)-1,Tr(·)和E(·)分别表示矩阵转置、共轭转置、共轭、逆运算、矩阵的迹和期望算子。
1 系统模型
假设对于一个上行链路多用户大规模MIMO系统,用户总数为K,随机分布在覆盖区域。基站为均匀线性阵列,配置M(M>>1)根发射天线。如图1所示。
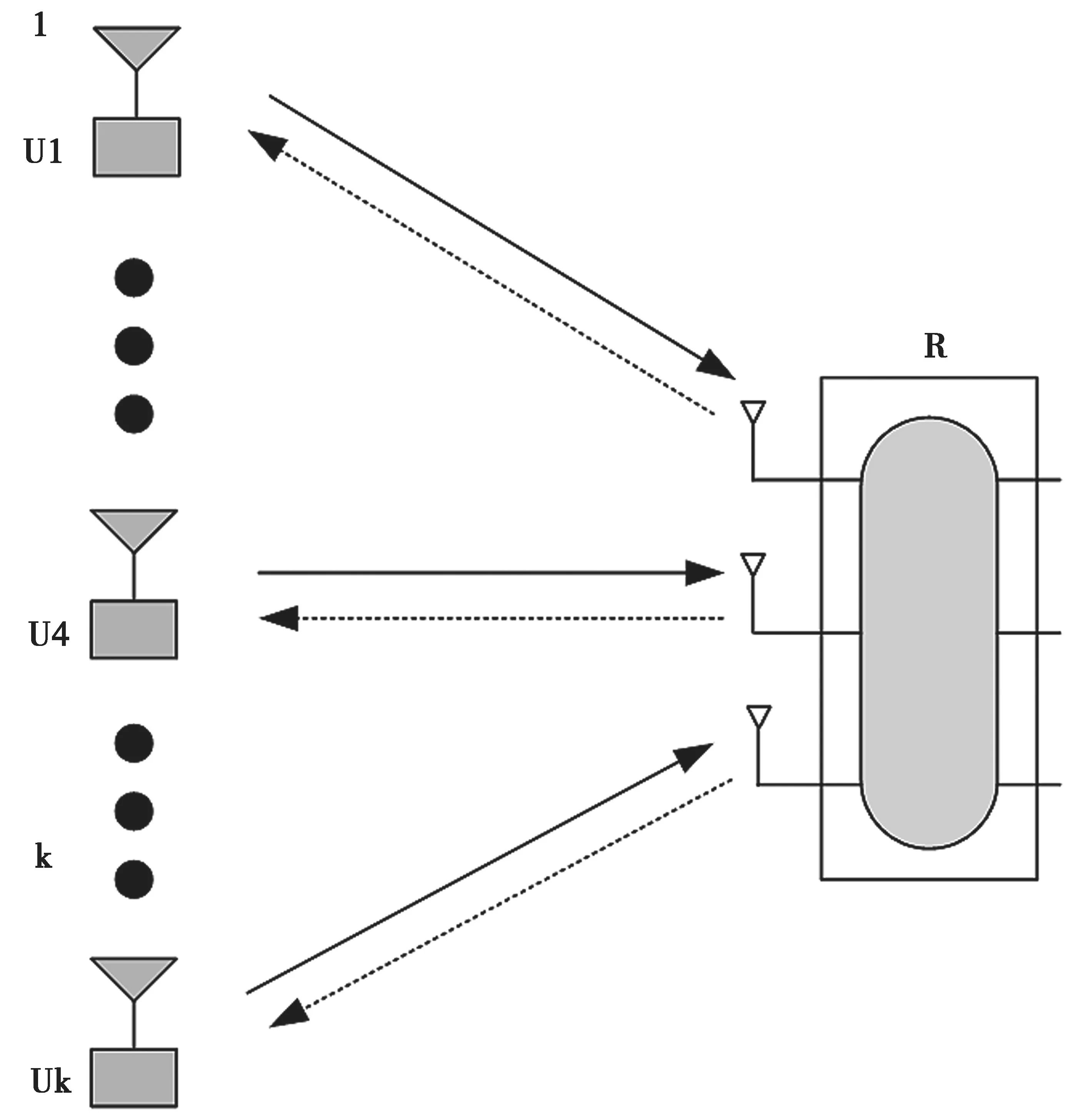
图1 上行链路莱斯信道系统模型示意图
根据莱斯信道模型,第k个用户与基站之间的信道向量hk为一个对应着LOS的直射分量路径和P个瑞利分布的随机分量路径叠加。若信道已归一化,即E{|hk|2}=1。则信道向量hk可表示为:
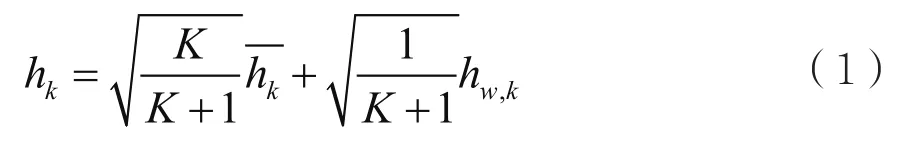
其中,K是基站与用户之间的信道莱斯K因子,即直射分量能量与瑞利分量能量之比。表示用户k的确定性分量,hw,k表示散射分量,其表示为独立同分布的零均值单位方差复高斯随机变量,且不同用户之间的随机成分是相互独立的。
若信道未归一化,则信道向量hk可表示为:
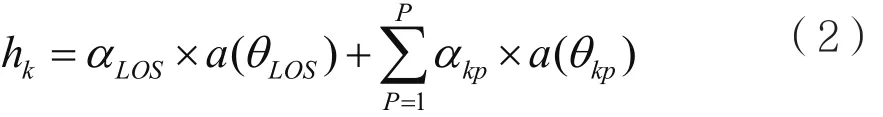
其中,P表示散射体反射到用户k的路径数,αLOS表示视距分量路径的复增益,αkp表示路径p的增益,天线阵列响应向量a(θkp) ∈ CM×1[2]表示为:
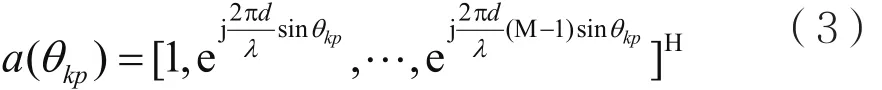
其中,d表示天线间距,λ表示信号载波波长,θkp表示路径p到达角,天线阵列响应向量示意图见图2。
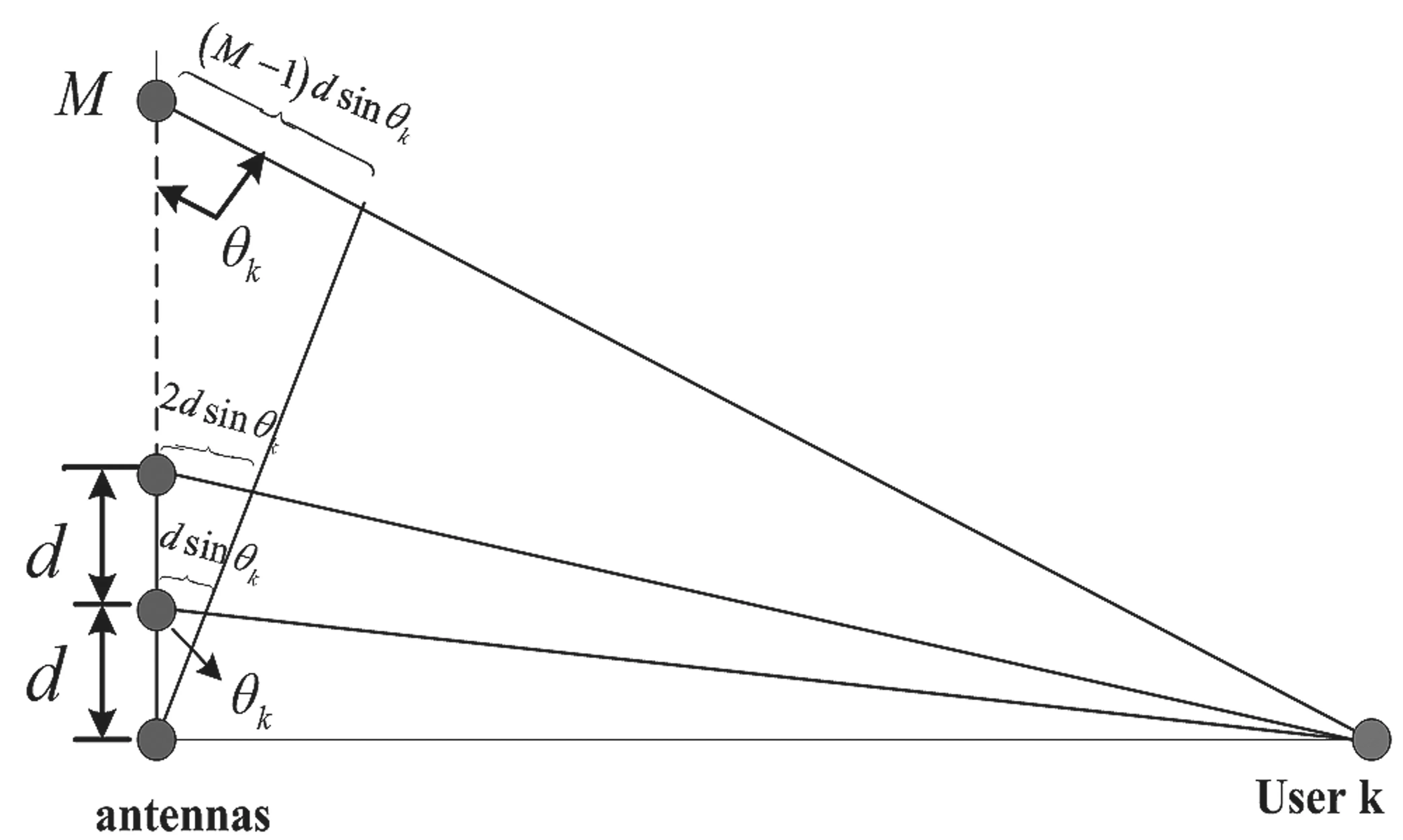
图2 天线阵列响应向量示意图
需要说明的是,若用户距离基站很远,所有天线对同一用户的到达角一样。假设用户k的到达角均值为 θk,角度范围为 [θk-Δθk,θk+Δθk],由于角度范围非常小,所以a(θkp),p=1,2,…,P之间相关性高,即用户k信道自相关矩阵是低秩的。
本文提出低秩特性的天线阵列理论,进一步降低信道估计的复杂性。由于a(θkp),p=1,2,…,P的高度相关性,hk可以先从有限正交基考虑。即:
其中,bq表示待确定的基,κq为其相应的系数,则估计hk中M个未知元素可以简化为只估计ν个常数κq。
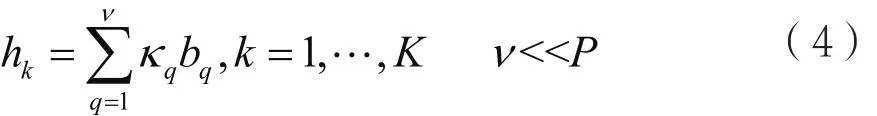
当两个向量越接近,则内积值越大。由于信道受到角度范围的影响,与离散傅里叶变换(Discrete Fourier Ttransform,DFT)内积后,占总功率比例大的点非常少而且集中。定义信道向量hk的DFT为:

其中,F为M×M的DFT变换矩阵,其第p行第q列元素为:

性质1:对于最简单的单路径场景,即P=1,hk=αka(θk),当M→∞时,只有一个非零点,这个非零点反映了能量的角度性。当M很大但不趋于无穷,的大部分能量仍然集中在这个非零点附近。
证明:
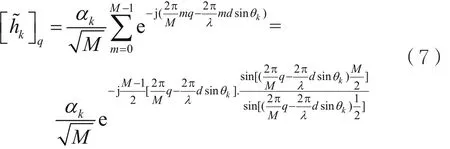
当M→∞时,式(7)可写为:
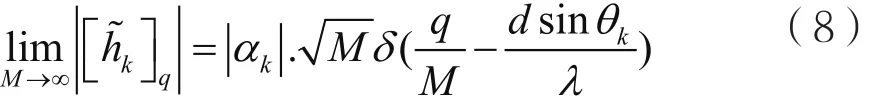
由 式(8) 可 得, 只 当 q0=Md sinθk/λ 时,,即非零点为q0,此时θk=arcsinq0λ/Md。
但当M很大但不趋于无穷时,可能会出现波束功率泄露的情况。而且,在大多数情况下,Md sinθk/λ不是整数,信道功率会从第个DFT采样点泄露到其他采样点。离散傅里叶变换是离散时间傅里叶变换a(θk)的离散样本,分别在取样点2πq/M,q=0,1,…M-1处对信道向量的DFT变换进行取样。因此, 的功率泄露程度与M成反比。当M很大但不趋向于无穷时,功率泄露现象并不严重,其大部分功率仍集中在Md sinθk/λ处。
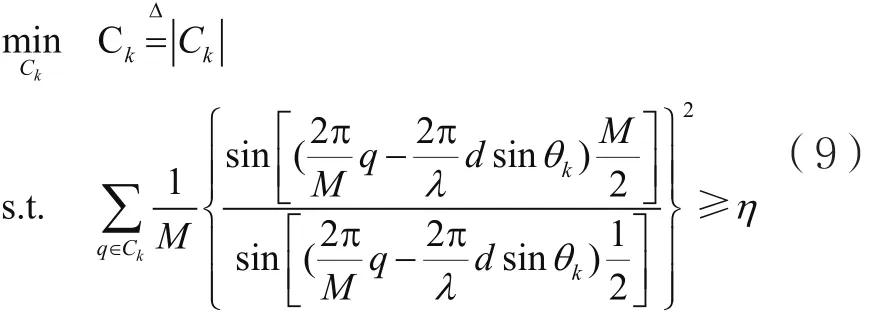
性质2:对于多路径场景,即P≠1,hk=当M趋于无穷时,仅在有限点取非零值,其对应的角度域为[θk-Δθk,θk+Δθk]。
证明:
基于式(8),考虑多路径信道,当M→∞时,每条路径都会映射到单一DFT点,则DFT变换对应的非零点的集合可定义如下:
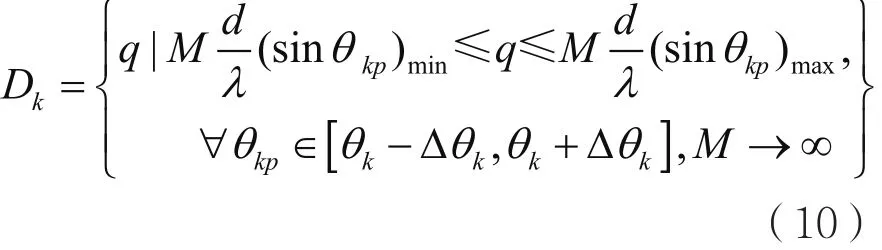
重新定义Dk为占信道总功率比例η的连续DFT点集合,则Dk上界为:
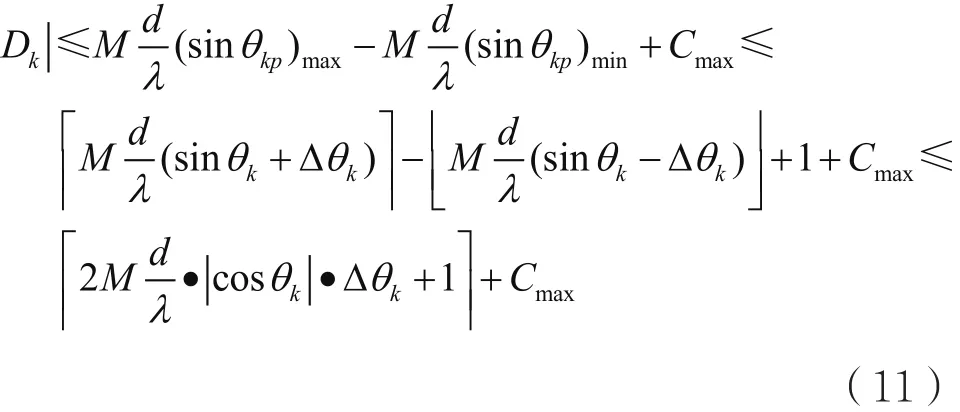
其中对于给定的η以及所有的θ∈[θk-Δθk,θk+Δθk],CmaxmaxCk。由于 Δθk很小,且:
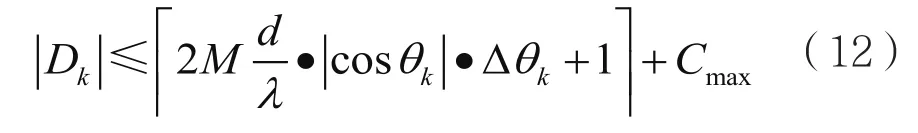
与M对比,其值仍很小,所以功率仍集中于少数几个点。根据以上的特性,可得以下推论:
推论:Dk反映了传入信号的平均到达方向和角度域扩展。所以,大规模MIMO的信道矢量可以用更少的参数定义:
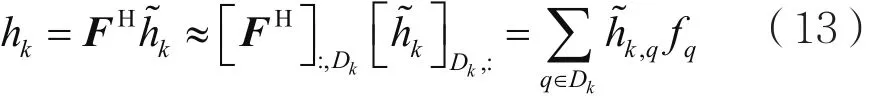
2 旋转角算法
定义:
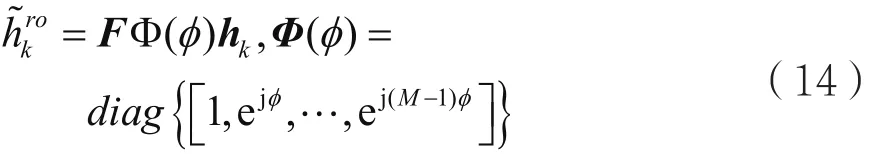
其中,φ∈ [-π/M,π/M],为空间旋转角。引入空间旋转角后,需使采样点能够采样到hk的DFT变换的最大值,而在其余采样点采样值为0。例如,在单路径的场景,对于某些整数q0,其到达方向角不为arcsin q0λ/Md,则存在功率损耗。定义一个新信道矢量=F Φ(φ)hk后,若 φk=(2πq0/M-2πd sinθk/λ),则由特性 1可知,只会在 q0=Md sinθk/λ取到一个非零值,减少了功率损耗。
在多路径场景下,功率损耗现象总是存在,但引入空间旋转角φ后仍有助于将能量集中在更少的DFT点上,即能减少功率损耗以及信道数量。我们定义连续点集使得占了总功率的η比例。可以在[-π/M,π/M]的范围内寻找一个合适的旋转角φ,使得最小。
为此,可以重新定义hk为:

其中,Φ(φk)Hfq,q∈D为新的等价基向量,且这些基向量相互正交。
综上分析,若莱斯K因子较大,则主要考虑主径,可忽略瑞利信道中P条路径的影响,近似为单路径场景。此时旋转角值为 φk=(2πq0/M-2πd sinθk/λ)。若莱斯K因子较小,莱斯信道主径效果不强,则此时 φk=(2πq0/M-2πd sinθk/λ)不再适用此情况,将在[-π/M,π/M]的范围内寻找一个合适的旋转角φ,使得|D|最小。本文采取的方法是将区间[-π/M,π/M]分为N等份,依次比较每一个旋转角度所对应的D,由此取到最理想的旋转角。由于[-π/M,π/M]角度范围小,所以其对应的复杂度也低。Φ(φk)hk可视为同时旋转正交波束,使得新的波束 Φ(φk)Hfq可更精确指向用户k。
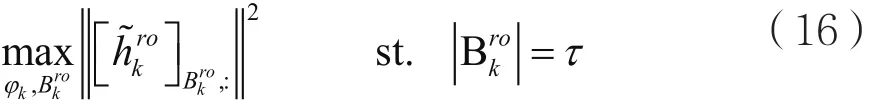
上述的优化可以通过在区间[-π/M,π/M]内进行一维搜索,对于每一个可能的旋转角φ,在的参数上移动一个尺寸为τ的窗口,使得最大化优化目标。
综上,寻找旋转角的总体方案如下:
(1)判断莱斯K因子是否大于阈值,若大于阈值,则旋转角通过 φk=(2πq0/M-2πd sinθk/λ)算出。
(2)若莱斯K因子小于阈值,则令φk=mπ/NM,(m=±1,±2,…,±N),在的参数上移动一个尺寸为τ的窗口,使得最大化优化目标。
3 信道估计
3.1 上行链路导频序列获得空间信息
假设在当前蜂窝网中分配τ<K个正交训练序列,τ<<K,长度L<T,T为信道相干时间。定义正交训练序列为:
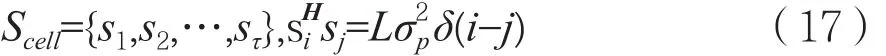
以第一组为例,基站收到的信号为:
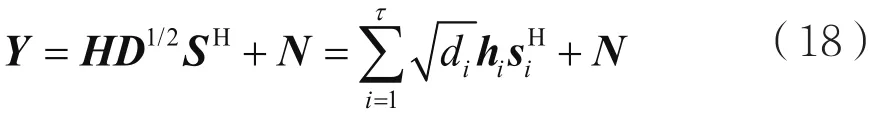
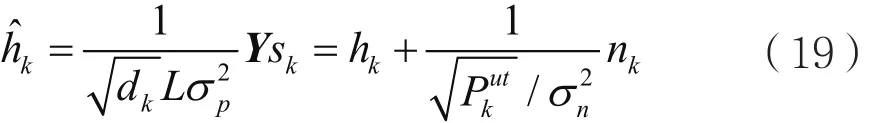
下一步,需获取最佳旋转角φk以及空间特征B。则信道矢量可表示为:
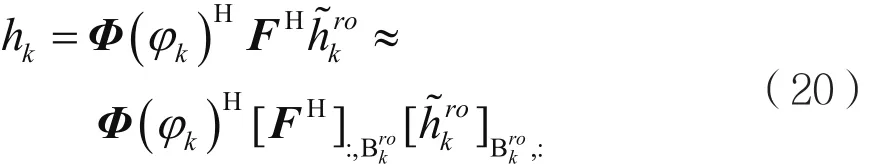
可见,相比于空间信道模型,本模型不需要信道协方差矩阵信息,只需长度为G×L的导频序列来获得用户空间信息。由于导频序列不频繁调用,所以开销相对小。
3.2 基于用户分组的上行链路训练
通过导频序列获得的信道信息只会持续一段很短的时间,成为一个相干时间T,在下一次传输时需要再次跟踪和估计。由于相干时间为毫秒级别,在这段时间内,可视为用户和它周围的散射体障碍物理位置近似不变。因此,在几个相干时间甚至几十个相干时间内,用户的到达角和角度域扩展可视为不变。例如,如果T=5 ms,则在10个相干时间内,以80 km/h运动的用户最大运动距离也只为1.11 m,即角度域变化可忽略不计。因此,每个用户的空间特征也可视为不变,则在接下来的传输过程中,只有需估计。
为消除导频污染以及只用τ个正交训练序列同时实现K个用户的上行链路训练,根据用户的空间特征将其分为不同组。若用户空间特征不重叠且中间隔着一个保护间隔Ω,将其分为同一组。即:
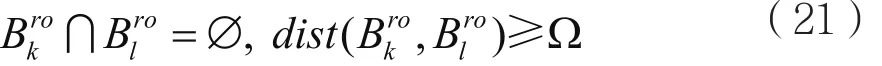
其中,dist(B1,B2)≜min|b1-b2|,∀b1∈B1,∀b2∈B2,保护间隔Ω长度取决于用户对导频重复使用[5]产生导频污染的忍受程度。根据上式分组规则,假定所有的用户分为了Gut组,定义U为第g组用户标号集合。由于τ=|B|与M相比很小,所以Gut<<K。由于同一组不同用户可根据其空间特征区分,因此对同一组所有用户使用同一个训练序列。不失一般性,考虑Gut≤τ,si为第i组(若Gut>τ,类似操作可在Gut-τ组中重复)。Gut组的K个用户同时发送其训练序列,则基站收到的信号可表示为:
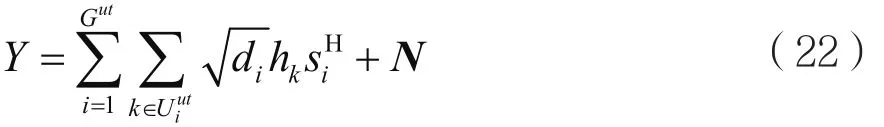
由于si之间相互正交,第g组的信号为:
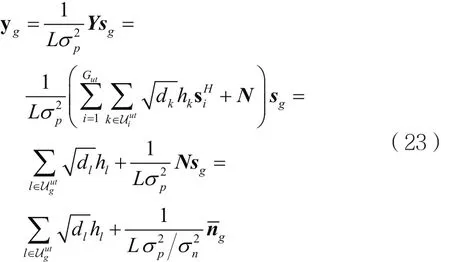
由式(22)可知,通过正交训练序列,来自其他分组的干扰完全消失。为导频污染,其产生是由于不同用户使用相同训练序列。但同一分组中的不同用户具有不同的空间特征B,我们可以分离同一组中不同用户空间信息,g组中用户k的信息为:
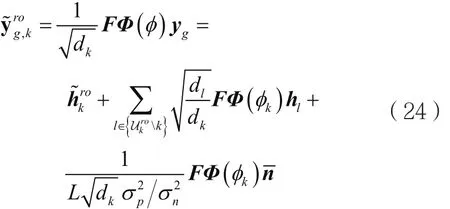
根据空间基扩展模型(Spatial Basis Expansion Model,SBEM)模型,近似为,提取为:
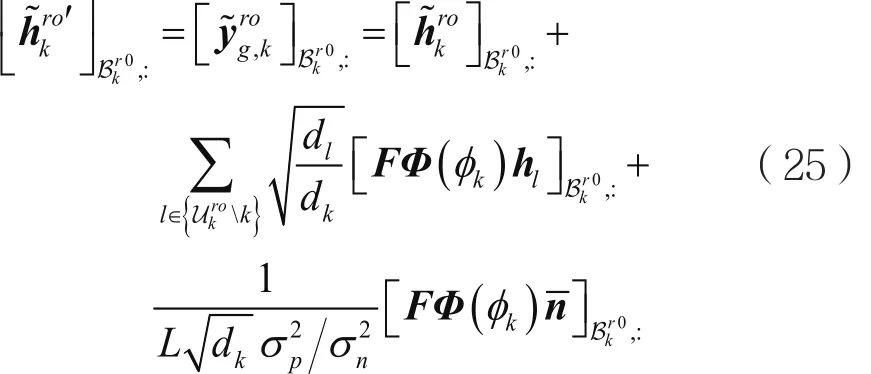
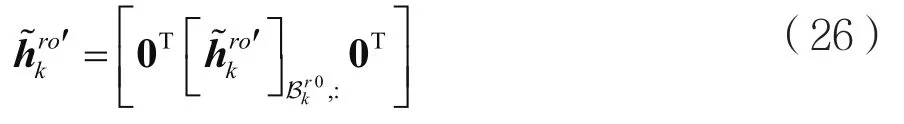
信道估计结果为:
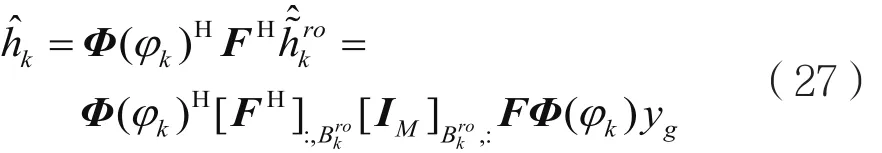
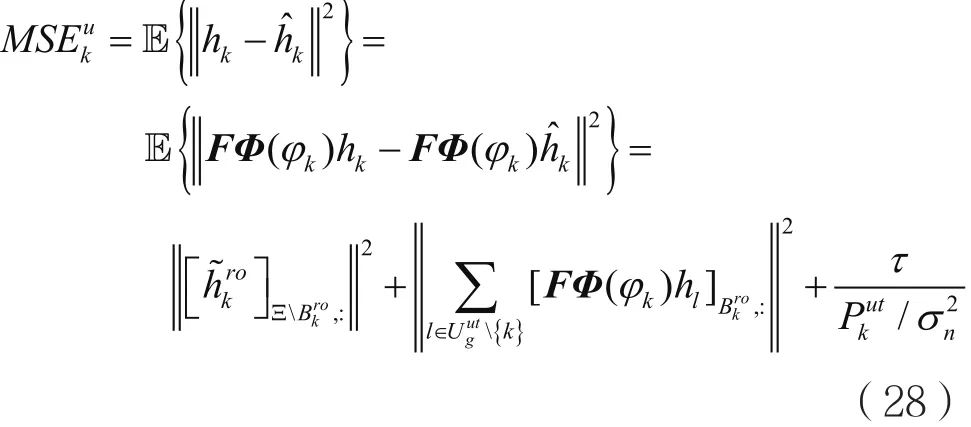
由式(28)可知信道估计误差包含三个部分,第一部分误差是由于SBEM模型中只取的τ个DFT点导致产生截断错误。由于导频污染,同组中的其他用户产生了功率泄露,这导致了第二部分的误差。噪声项产生了第三部分的误差,该误差与τ成正比。若用户的角度域变小或者τ变大,截断错误产生的误差可以减小。但是,角度域是由于环境的固有属性,τ则是根据标准制定的,这两者都不可控。若保护间隔Ω变大,则用户间相互干扰也会减小。因此,若Gut比τ小,我们就规定Gut=τ,以便平均分配每个组的用户,从而减小第二部分误差。
4 用户分组
根据前述推导,设计一种分组方案:
令天线数M=128,天线间距d=λ/2,用户数K=32,P=100,路径增益αkp对所有路径和用户都服从高斯分布,角度域θkp的范围为[θk-Δθk,θk+Δθk],Δθk=2°,系统相干时间T=128,τ=16(其为天线数的1/8),保护间隔Ω=τ/4=4,导频长度L满足16≤L≤128,分别取L=163 264。信噪比(SNR,Signal-Noise Ratio)ρ=σ/σ,信道估计的性能指标为:
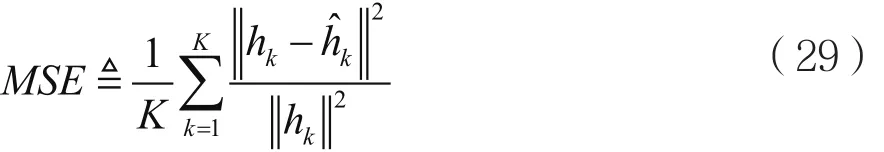
假设32个用户对应的角度θk如下表所示,由算出其对应的q,即DFT变换的第q个点,如表1所示。

表1 各用户所对应的q
第1组:(13,21);第2组:(14,22);
第3组:(12,23);第4组:(11,24);
第5组:(10,25);第6组:(9,26);
第7组:(8,27);第8组:(7,28);
第9组:(6,29);第10组:(5,30);
第11组:(1,15);第12组:(2,16);
第13组:(3,17);第14组:(4,18);
第15组:(19,31);第16组:(18,32)。
5 波束成形矩阵及分组优化算法
根据用户空间特征将用户分为不同组,以便在后续数据传输期间提高频谱效率。根据SBEM模型设计的波束成形矩阵为:
对于第g组的第k个用户,其信号为:
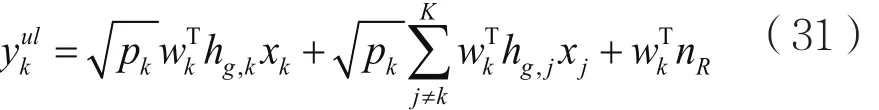
其中,pk表示用户发射功率,为期望信号,为同组用户相互干扰,wnR为噪声。则第g组的可达速率为:
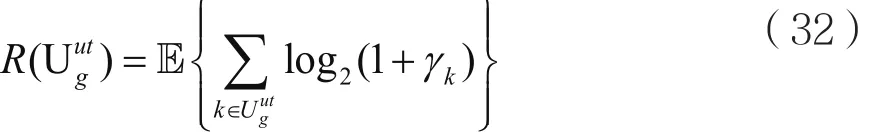
其中,信噪比γk为:
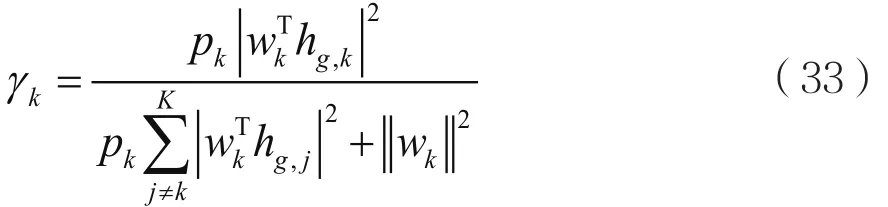
基于最大化可达速率的目标,即:
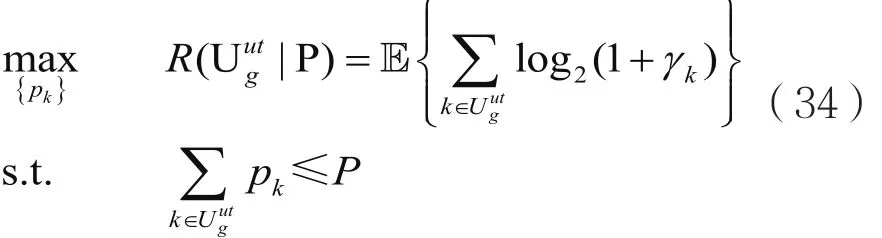
其中,P为第g组的总功率。本文提出的优化算法如下:
步骤3:对于第g组,在Ur集合中选择欧几里得范数最大的用户,即 l´=arg maxl∈Ur||||。令P=ρ,U=U∪ {l´},Ur=Ur{l´}。并通过式(33)算出R(U|P)。
步骤4:选择Ur集合中空间特征不重叠的用户,并将其分为一组,记为U´g。即U´g={m∈Ur|B∩
步骤 5:若 U´g≠∅,则 P´=P+ρ。在 U´g中找到一个用户m´,使
步骤7:当算法结束时,当前g的值即为最小组数Gut。最优用户调度结果为U1,U2,…,UGut。
6 仿真和分析
6.1 仿真环境与方法
在Matlab的仿真环境中,对系统性能进行仿真验证[7]。
所有仿真系统环境设置如下:
令天线数M=128,天线间距d=λ/2,用户数K=32,路径数P=100,路径增益αkp对于所有路径和用户都服从高斯分布,角度域θkp的范围为[θk-Δθk,θk+Δθk],Δθk=2°。
6.2 仿真结果分析
6.2.1 莱斯信道系统模型与信道特性
(1)莱斯信道与瑞利信道的比较
图3(a)表示瑞利信道分布,图3(b)表示莱斯信道分布。由图3可见莱斯信道主径效果明显。
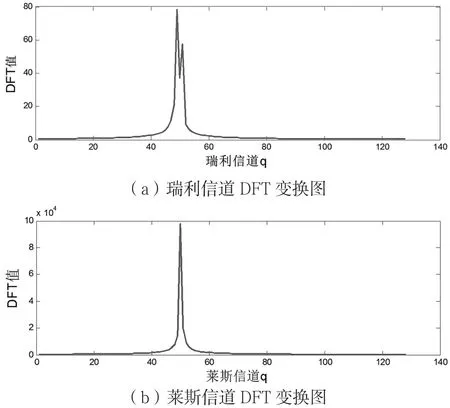
图3 瑞利信道与莱斯信道DFT变换图比较(θk=50.2°,Δθk=2°)
(2)连续函数的最大值
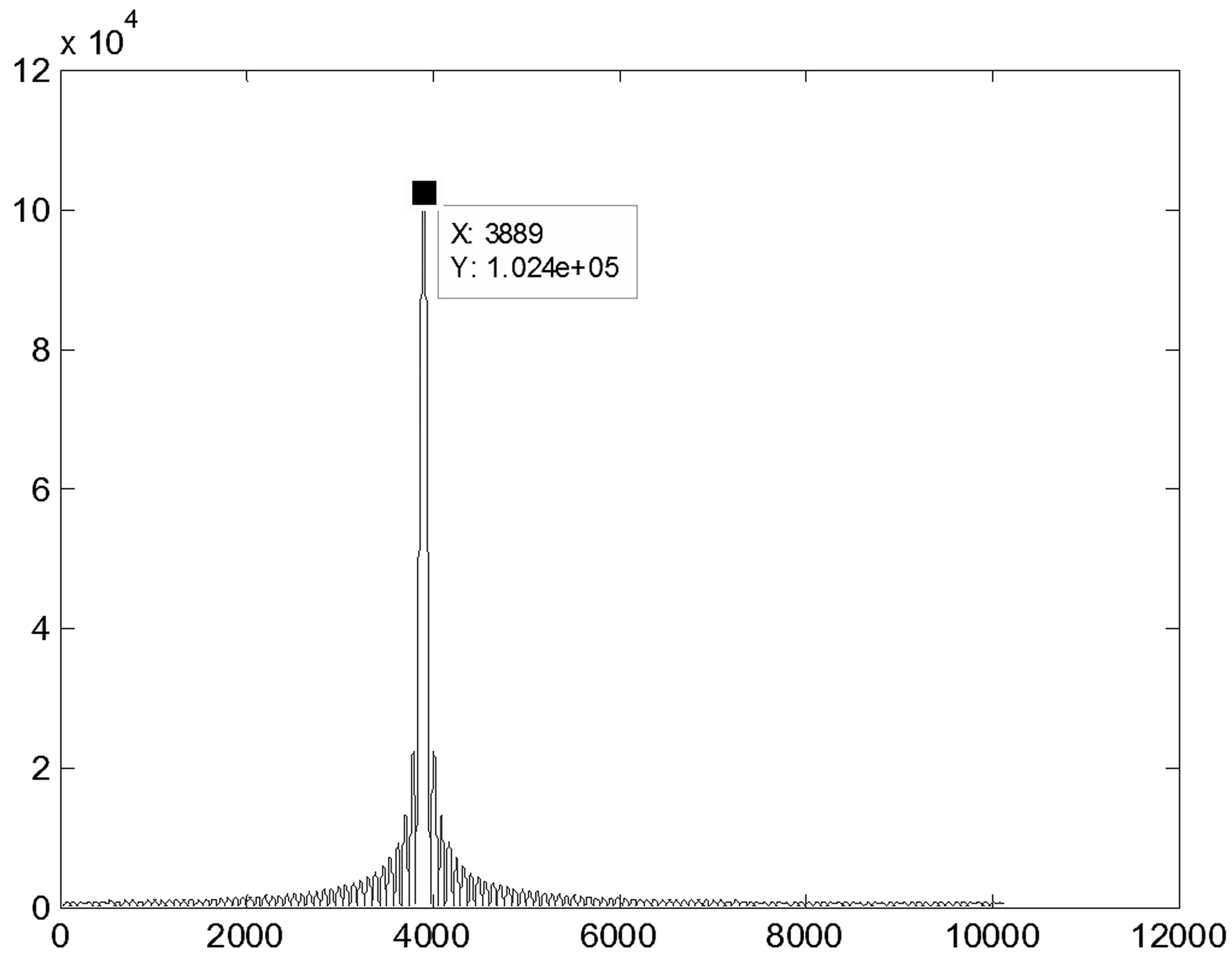
图 4 过采样情况下 DFT 变换图(θk=50.2°,Δθk=2°)
由于DFT是离散样本,为得到最大值,则需进行过采样。图4为过采样情况下莱斯信道下DFT变换的图形,由图知最大值为1.024×105。
(3)旋转角的引入
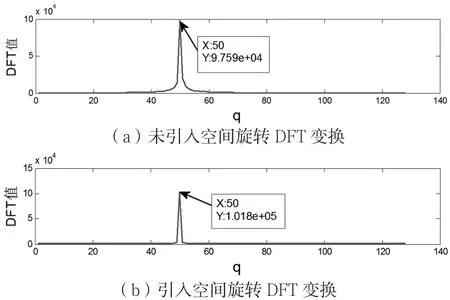
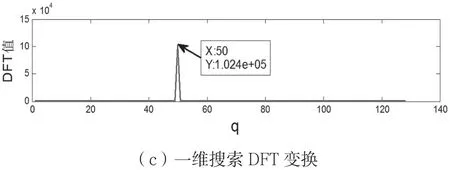
图5 未加旋转角与引入旋转角最大值比较(θk=50.2°,Δθk=2°)
图5 (a)为未加旋转角情况下hk傅里叶变换,可知功率 集 中 于q=Md sinθk/λ=128sin(50.2°)/2 ≈49.17附近,此时||最大值为 9.759×104。图 5(b)为引入了旋转角 φk=2πq0/M-2dπsin θk/λ=π×49/64-πsin(50.2°)≈-0.0084后的DFT变换,由图可知||最大值为1.018×105,还未达最大值。图5(c)为一维搜索后找到最佳旋转角后的DFT变换,由图知||最大值为1.024×105,达到最大值。
将图5中未加旋转角的DFT变换与经过一维搜索并引入最佳旋转角后的DFT变换置于同一张图,如图6所示。由图知引入旋转角后功率更加集中,能够采样到||的最大值,而其余采样点采样值为0,有效消除干扰。

图6 未加旋转角与引入旋转角采样点采样值的比较
6.2.2 信道估计系统
根据本文第4节所述分组方案仿真结果如图7所示。由图7可得以下3个结论:
(1)由于训练总功率正比于L,随着训练序列长度L的增大,上行链路均方误差性能变好。
(3)由于引入旋转角后可以将信道功率集中于更少DFT点,减少点集B外其余点的功率泄露,因此可以减小SBEM模型中的截断错误,这在高信噪比、截断错误占据主导位置时表现尤为明显,由图7可知,MSE最小值由未引入旋转角时的0.07变为0.03。但在低信噪比时、噪声占据错误主导位置时,引入旋转角效果就不显著。
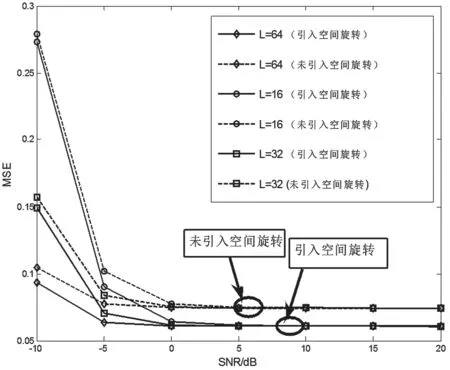
图7 不同L情况下未加旋转角以及引入旋转角后信道估计
6.2.3 波束成形矩阵的设计与数据传输
图8显示未经优化的分组方案,即平均分配各组用户,引入旋转角前后的可到达速率以及经过优化算法后引入旋转角前后的可到达速率。
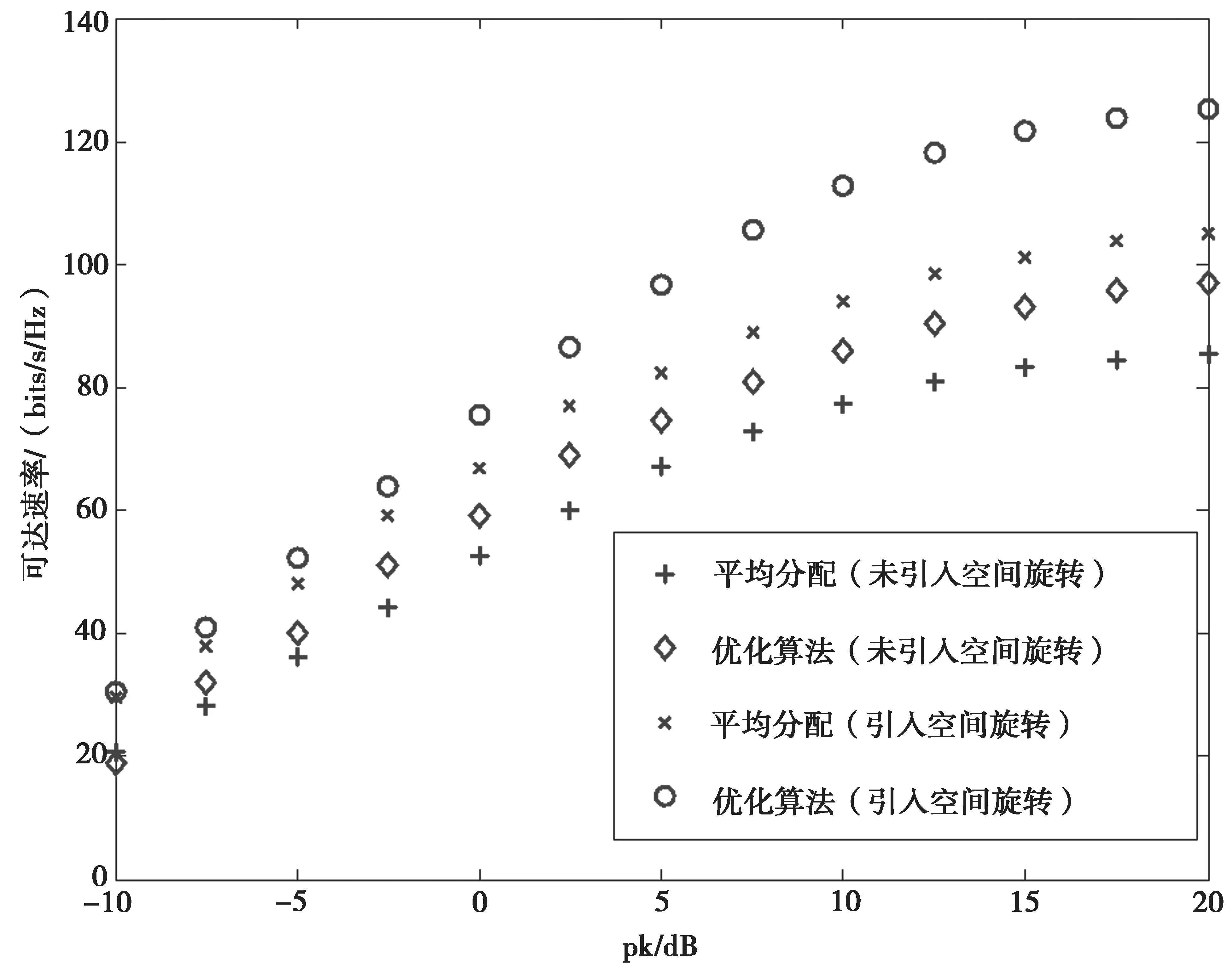
图8 平均分配各组用户及优化算法的可达速率性能
可得出以下3个结论:
(1)随着每个用户发射功率的上升,系统可到达速率性能上升,但是会有上限。这是由于用户间存在相互干扰,影响可到达速率的进一步提升。
(2)不论有无引入旋转角,由于经过优化后的算法用户间干扰减小,所以可到达速率比起平均分配各组用户方案进一步提升。
(3)不论是平均分配各组用户还是经过优化算法,引入旋转角后其可到达速率性能均得到提升。
7 结 语
本文研究了大规模MIMO波束成形方法,利用波束域信道估计降低信道维度,引入旋转角算法,减小功率泄露,并利用用户分组算法提高用户可达速率。结果显示,当使用旋转角算法和分组算法后,信道估计MSE性能和用户可达速率得到较大提升。
