从香农公式再看直扩通信与通信干扰之间的博弈*

石 荣，杜 宇

（电子信息控制重点实验室，四川 成都 610036）

0 引 言

通信干扰是通信对抗中电子攻击的重要手段，其主要目的是要降低通信双方信息传输的有效性，甚至完全阻止通信传输的发生；而通信抗干扰传输是通信对抗中电子防御的主要手段，即采取一切必要措施与途径来提升信息传输的有效性，降低通信干扰所带来的影响[1-2]。由此可见：通信干扰与通信抗干扰传输是矛盾对立的两个方面，相互之间的博弈与对抗是长期存在的，这一点在直接序列扩频抗干扰传输与对直扩通信实施干扰的应用中表现得尤为突出[2]。直接序列扩频通信至诞生以来一直是军事通信抗干扰的主要技术手段[3-5]，从早期的周期性短码扩频，发展到周期性长码扩频，现在具有无限不循环长码扩频的直扩通信也开始逐渐应用[6-7]。在对直扩通信进行干扰的研究中各种干扰样式近年来也被各类公开文献所提出，并进行了广泛的研究与探讨，在侦察干扰方面形成了一系列针对周期性扩频短码与周期性扩频长码的研究结果，极大地提升了干扰攻击的有效性[8-9]。

但是在上述研究过程中对无限不循环长码扩频信号的干扰与抗干扰的研究结果很少，而无限不循环长码扩频正是未来直扩通信的重点发展方向。针对这一问题，在对经典的香农公式及其物理意义简要回顾之后，针对直接序列扩频通信所具有的类噪声传输特性，通过在香农公式中扩展引入干扰信号分量，从而定量描述了在通信干扰条件下直扩通信链路的信道容量，展现了通信干扰实施方与通信抗干扰传输方在信道容量控制争夺中的博弈过程。在此基础上分析了无限不循环长码直扩通信通过降低信息传输速率，提升扩频处理增益，从而在理论上可实现直扩链路信息传输永不断链的应用潜力。另一方面，这也催生了未来通信干扰与抗干扰的新型应用模式：即在干扰中通信与在通信中干扰，这也为二者之间的博弈关系的演绎提供了新的诠释，从而为该技术方向上通信对抗中攻击与防御关系的研究提供了新的参考，详细阐述如下。

1 香农公式与信道容量

1948年美国贝尔实验室的香农教授发表了《通信的数学原理》的学术论文，提出了著名的香农定理：在带宽为B（单位：Hz）的信道上噪声功率为N（单位：W），信号的功率为S（单位：W），那么该信道能够传输的最大信息速率C（单位：bps）在理论上如下式所表达，同时C也被称为该信道的信道容量。

式（1）又被称为香农公式，其中N0为单位带宽内的噪声功率，单位：W/Hz或J（焦耳）。在这篇经典论文中香农指出：如果在一个信道上传输信息，只要实际的信息传输速率Creal不超过C，那么总可以找到一种方法来获得无差错的准确传输。

在实际应用中传输信道的单位带宽内噪声功率N0通常保持恒定，N0又被称之为噪声功率谱密度。如果在信号功率S保持一定的条件下，信道容量C与传输带宽B之间的关系曲线如图1所示，图中以S/N0=20 000为例进行曲线绘制。

图1 信道容量与传输带宽之间的关系曲线

由式（1）可推导出在B→∞时信息传输的香农极限：

由式（2）可知：信道传输容量C存在一个上限，这一点从图1的信道容量与信道带宽之间的关系曲线也得到了验证。图1中实线是式（1）所示的曲线，虚线是实线对应的渐进线，由式（2）计算，其数值为20000/ln 2≈28.854 kbps。由此可见，在信号功率与单位带宽内的噪声功率之比保持一定的情况下，通过扩展带宽的方式不能无限制地提升信道容量，信息传输速率的上限会受到香农极限的限制。

4.律师调解达成调解协议的司法确认案件总量少。截至2018年6月底，全市律师调解案件申请司法确认的为90件，只占律师调解成功案件数872件的10.32%。

香农公式之所以长期以来如此引人注目就在于香农自己开了一个很好的头，指出总之存在一种方法与技术途径可以逼近这一上限，但是至于是哪种方法，香农自己也没有完全研究清楚。也正是于此，在香农的指引下，在该方向上吸引了大批的后来者在寻找可能的技术方法途径的道路上前仆后继、奋勇前行，当然也获得了很多的研究成果，在此不再展开赘述了。

2 通信干扰对信道容量的影响

如前所述，虽然香农公式描述了在信道中存在噪声条件下的信道容量，但是干扰信号与噪声信号具有不同的特性，在信道中存在干扰条件下是否可以沿用香农教授的模型，需要针对具体问题进行具体分析。对于直接序列扩频通信信号，特别是无限不循环长码直扩信号来讲，在扩频处理过程中本身就具有类噪声的特性，其扩频序列也被称为伪随机序列；另一方面，直扩信号在自身解扩过程中对信道中干扰信号的作用又相当于一个扩频处理过程。鉴于直扩信号的上述特有性质，在本文中我们以无限不循环长码直扩信号为研究对象，将信道中的干扰近似看成是一种特殊的信道噪声，沿用香农教授的数学模型，那么在有干扰条件下的信道容量CJam可近似表示为：

其中，Ja表示该信道中干扰信号的平均功率，单位W，Ja,0=Ja/B表示单位带宽内的平均干扰功率，单位：W/Hz或J（焦耳）。式（3）可以看作是针对无限不循环长码直接序列扩频信号的扩展香农信道容量公式，下面就以此为基础，分别讨论在信道带宽不受限与受限条件下的信道容量。

2.1 在信道带宽不受限条件下的信道容量

由式（3）可知，在单位带宽内噪声功率N0、信号功率S和干扰信号功率Ja保持一定的条件下，信道容量CJam与传输带宽B之间的关系曲线如图2所示，图中以S/N0=20 000，S/Ja=0.1为例绘制曲线。图2中实线是式（3）所示的曲线，虚线是实线对应的渐进线，数值同样为20000/ln 2≈28.854 kbit/s，为了进行对比，将式（1）所示的无干扰条件下的信道容量曲线也绘制于图2中用点划线表示。

图2 干扰条件下信道容量与传输带宽之间的关系曲线

由图2可见：在信道带宽不受限的条件下由式（3）可推导出在B→∞时信息传输的香农极限：

对比式（2）与式（4），并结合图2可知：干扰与噪声对信道容量的影响是完全不同的，由于接收机中的噪声是普遍存在的，且噪声功率谱密度N0保持恒定，随着接收带宽的扩展，进入接收机中的噪声总功率也是线性增加的，从而使得信道传输容量存在一个上限。但是对于一个特定的干扰信号而言，其干扰信号总功率是保持固定的，随着接收带宽的扩展，干扰信号的功率谱密度Ja,0是随之递减的。由式（3）可知，当干扰功率谱密度递减到噪声功率谱密度N0之下时，其对信道容量的影响也会被噪声的影响所掩盖，所以当带宽B扩展至较大时，干扰的影响会变得很微弱。这也是直接序列扩频通信中不断追求更宽带的扩频处理的重要原因所在，从理论上讲，如果无限制地扩展扩频带宽，那么干扰信号的作用会被无限制地消减下去。

在实际应用中30 GHz以下的微波射频频段可利用的频谱资源十分有限，工程上无法实现传输带宽如理论所述的大幅度扩展，但在100 GHz至100 THz的太赫兹频段，传输带宽的大幅度扩展是完全可能的，现在扩频带宽超过10 GHz的直接序列扩频通信已经实现。由此可见，扩展之后的香农公式在理论上指出了在太赫兹频段的信息传输的有效抗干扰手段即是超宽带的扩频传输。

2.2 在信道带宽受限条件下的信道容量

如果将干信比Ja/S看成一个整体，当信号功率S保持定值时，随着Ja的逐渐增大，(Ja/S)-1将逐渐趋近于零，于是有式（6）成立：

将式（5）与式（6）所示的曲线分别绘制成实线与虚线于图3中，图中取B=1 MHz为例进行曲线绘制，为了更加清晰地表示，图3中横纵坐标均采用对数刻度。

图3 信道容量与Ja/S之间的关系曲线

由图3与式（6）可知，在确定的信道带宽B条件下，随着干扰功率Ja的逐渐增加，信道容量CJam与干信比Ja/S成反比例关系减小。这也就意味着：从理论上讲，对一条直扩通信链路实施干扰，可以使该链路的传输速率尽可能地降低，但并不是这条链路上一点信息也传输不了，即无论干信比如何大，在遭受干扰的通信信道上总是可以进行信息传输，且传输速率的上限由式（6）所描述。

上述理论分析结果给出了一个结论：即采用无限不循环长码直接序列扩频手段，无论干扰信号如何大，通信方始终能够进行信息的传输，实现永不断链，只是传输速率下降而已。关于这一点，接下来我们还要继续讨论。

3 通过降速传输实现永不断链

如前所述，在现今的微波射频频段的通信传输应用中，传输带宽受到各种工程应用条件与自然传输条件的限制，不可能大幅度地扩展，例如：短波通信手段的传输频段范围就限制在3～30 MHz范围内，卫星通信的传输频段宽度同样也受限于卫星平台上搭载的转发器的带宽等。由前一节的理论分析可知：在信道带宽受限条件下，虽然信道容量与干信比成反比，但始终不会等于零。这从理论上意味着总可以找到一种方法来实现通信链路的持续信息传输，也就是所说的永不断链。这一点与我们当前的工程实际情况有一些差异。

当前在工程实际应用中从短波通信到超短波通信，从移动通信到散射通信，从数据链传输到卫星传输，上述各种各样的通信链路都会遭受不同程度的干扰。在干信比较小时，数字通信链路首先表现出来的就是产生不同等级的误码，例如误码率从10-5到10-1变化。随着干信比的逐渐增大，通信链路便会产生位同步、载波同步等同步失锁，造成链路传输完全中断。通信链路的完全中断意味着没有任何一点信息能够从通信发送端准确地传送到通信接收端，哪怕1比特的信息都没有，即通信传输的流量为零。这对于很多应用，特别是军事通信应用来讲是非常致命的。在现代军事战场上一条简短的指令信息也许仅仅只有几十个比特，但是在通信链路完全中断的情况下，这几十个比特的信息就始终无法传送到预定的接收处，这对于战场指挥控制来讲简直就是致命的，甚至可能导致整个战役的失败。

由上可见，对一条通信链路实施干扰，随着干扰功率的加大，链路从产生误码到链路中断的状态变化并不平滑，其中有状态突跳的发生。这一现象与前述扩展香农公式给出的理论结果存在差异。产生这一差异的主要原因在于：工程应用中的通信收发信机的设计几乎都是按照几个恒定传输速率来进行设计的，一旦遭受干扰，当给定信道上的信道容量小于通信收发信机中所设计的几个传输速率时，那么在理论上就已经无法确保准确的传输；而此时，通信收发信机的硬件设计是固定的，无法改变预先设计的传输速率，造成这一速率的信息传输无法维持而中断，断链之后一点信息也传输不了。

如要改变上述情况，就需要在工程实现上采用自适应降速传输的通信收发信机的设计，即根据式（5）或式（6）所给出的在干扰条件下的信道容量，自适应地降低通信传输速率，从而使得无论有多么强的干扰，通信链路将永不断链，持续传输，降低的仅仅是传输速率而已。实际上在当前技术阶段，采用无限不循环长码扩频的恒定扩频码速率的直接序列扩频技术就能在一定程度上达到上述目的。设信道传输带宽为1.2 MHz，直接序列扩频信号采用滚降系数为0.2的平方根升余弦成型滤波，扩频码速率为1 Mcps的BPSK调制，信息码速率设计成可以根据外界干扰信号的功率而灵活可调的模式。举例如下：

如果在1.2 MHz的信道带宽内的干信比Ja/S=20 dB，由式（6）计算出的信道容量CJam≈17.312 kbit/s，此时设计数据速率为0.5 kbit/s，扩频处理增益33 dB，这样即可确保链路以0.5 kbit/s的速率维持通信，而不会断链。

如果干信比Ja/S=40 dB，由式（6）计算出的信道容量CJam≈173.12 bit/s，此时设计数据速率为5 bit/s，扩频处理增益53dB，这样即可确保链路以5 bit/s的速率维持通信，也不会断链。

当干扰功率进一步升高，干信比Ja/S=60 dB，由式（6）计算出的信道容量CJam≈1.7312 bit/s，此时设计数据速率为0.05 bit/s，扩频处理增益73 dB，这样即可确保链路以0.05 bit/s的速率维持通信，仍然不会断链。虽然0.05 bit/s的速率意味着20 s的时间内才能传输1 bit的信息，即便是这样的速率，在战场指挥的关键时刻，仍然是能够传输关键的指挥控制指令的，这样的速率总比任何信息也传输不了要强了许多。

上述示例也揭示出：在未来的通信收发信机的设计上，通过软件加载重构方式设计出降速率传输模式，即可在现代信息化战争中实现通信链路永不断链的降速传输新应用。当然在通信收发信机的硬件设计上也需要全面考虑信号接收的巨大动态范围，确保接收机不饱和，在强干扰信号条件下能够使强信号与弱信号都得以接收，从而为后续通过软件上的数字信号处理提取出微弱信号提供条件。这样一来，将改变传统的通信对抗博弈的观念，在未来的直扩通信干扰中，通过干扰只能降低一条直扩通信链路的信息传输速率，但是不会造成该条直扩通信链路的完全中断。

4 在干扰中通信与在通信中干扰

随着电磁空间中用频设备的激增，有限的电磁频谱资源必将成为各方争夺的焦点。前面通过扩展香农公式的分析展示了直扩通信方与通信干扰方之间对信道容量控制的博弈过程，而其中调控因素之一就是双方的信号功率。在未来的电磁空间作战中追求的目标之一就是：确保我方的行动自由，而限制敌方的行动自由；就通信而言，就是在有限的电磁频谱中确保我方能够传输信息，而限制对方的信息传输，成为双方关注的焦点。但是在双方电子设备的发射功率都有限的条件下，用多少功率去自己通信？而用多少功率去干扰对方的通信？这成为双方对抗博弈的关注点[10]。其中一个全新的思路就是在我方进行通信的同时，实现对敌方通信的干扰，即在确保我方信道容量的同时，尽可能地降低敌方的信道容量。

由前述分析可知：决定信道容量的关键因素是带宽和带宽内的干信比。在带宽保持一定的条件下，干信比越大，通信信道的容量越小。如果对抗双方（分别记为A与D）都在同一个带宽为B的通信信道进行信息传输与干扰攻击，双方的信号功率分别为SA和SD，且二者远大于信道内的噪声功率N，于是双方在该信道上的信道容量CA和CD分别为：

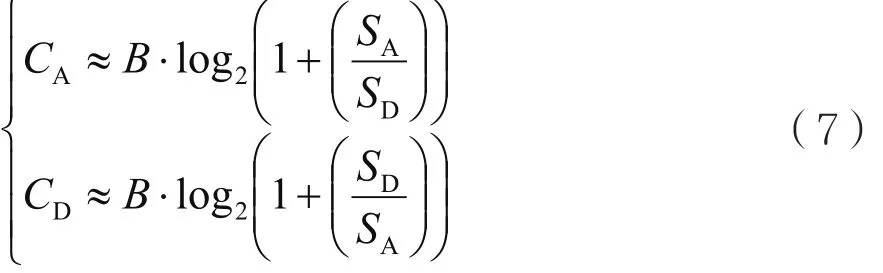
对比式（7）与式（5）可知：对于通信方A来讲，通信方D的信号是干扰信号；对于通信方D来讲，通信方A的信号是干扰信号。通信方A既在该信道上进行通信传输，同时对通信方D也实施了干扰；反过来，通信方D既在该信道上进行通信传输，同时也对通信方A实施了干扰，这在通信方A与D都采用无限不循环长码的直接序列扩频通信信号的情况下是完全可实现的。这实际上也反映了在干扰中进行的通信，以及在通信中实施干扰的一种技术途径，即发挥了一举两得和一石二鸟的作用。在不同的双方信号功率比条件下，对抗双方的信道容量CA和CD如图4所示，图中CA用虚线表示，CD用实线表示，图中以B=1 MHz为例进行曲线绘制，横坐标为两个信号之间的功率比SA/SD，为了显示方便，横纵坐标均采用对数刻度。

图4 对抗双方信道容量与功率比之间的关系曲线

由图4和式（7）可知：当对抗双方的信号功率相等时，双方的信道传输容量相等CA=CD，且在数值上均等于信道带宽B。随着功率比差异的增大，大功率一方的传输容量将随功率比成对数形式增大，而小功率一方的传输容量将随功率比成比例下降，在此情况下，大功率的一方在通信传输的同时，也实现了对小功率一方的压制干扰。由此可见：图4和式（7）反映了对抗双方之间在信道容量上的控制争夺的博弈过程。

式（7）仅仅对两方对抗的情形进行了建模描述，如果在同一个信道带宽内存在多个对抗方Ai时，i=1,2,…,M，M为该信道上的使用方的总数，记带宽内各方的信号功率分别为Si，且这些功率均远大于信道内的噪声功率N，那么对于任何一方Ai来讲，其信道传输容量Ci近似由下式所表达：

式（8）揭示在多方博弈条件下，各方要实现在通信中干扰，以及在干扰中通信的信息传输速率的上限，以及各方电子设备功率的控制关系。除了前面所举的各方都采用无限不循环长码的直接序列扩频信号之外，还可以设计其它的信号形式来达到在通信中干扰与在干扰中通信的目的。这实际上也引出了一个全新的方向，即通信与干扰一体化波形设计，这也是值得我们后续继续深入开展研究的内容。

5 结 语

由扩展的香农公式可知：从理论上讲，一条通信链路是不能完全阻断的，只能尽可能地使其信道传输容量无限减小，但该通信链路仍然能够实现极低速率的信息传输。通过采用无限不循环长码直接序列扩频通信可以在实际工程应用中逐渐接近这一理论目标，即通过降低信息传输速率实现永不断链的通信。实际上这也展现了通信抗干扰传输方与通信干扰实施方在信道容量控制争夺中的博弈过程，同时也引发了在干扰中通信与在通信中干扰的新型应用模式，牵引出了通信与干扰一体化波形设计的新的研究方向。本文对上述问题进行了详细的分析与探讨，所提出的部分观点与研究结果也为通信对抗中攻击与防御新型关系的建立提供了参考。