OFDM系统非平稳相关散射突变信道的表示与估计*

谢文武 ，廖俭武 ，王 俊 ，朱 鹏 ，余 超

（1.湖南理工学院 信息科学与工程学院，湖南 岳阳 414006；2.武汉虹信通信技术有限责任公司，湖北 武汉 430079）

0 引 言

近年来，我国的高速铁路建设规模不断的增加，高铁成为了人们日常生活中主要的交通工具之一。然而，随着列车的行驶速度不断的提升，势必会带来较大的多普勒频移，信道表现为快衰落特征，它们将会破坏正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）子载波之间的正交性，引起载波间干扰（Inter-Carrier Interference，ICI）。另外，由于高速铁路的周边环境复杂多变，有城市、平原和隧道等，这些物理环境对无线信道的影响不同，高铁在穿过这些环境时信道特性会产生突变，信道就转变为非广义平稳相关散射（Non Wide-Sense Stationary with Uncorrelated Scattering，Non-WSSUS）信道[1-3]。由于以上这些高铁信道的特点，将为车地通信控制和乘客的宽带无线数据接入业务带来很大的挑战，为了满足高铁车地通信的高移动性和高可靠性，有必要对高速铁路的信道模型和估计方法进行研究。

OFDM技术作为3GPP长期演进（Long Term Evolution，LTE）的核心技术，通过一系列相互正交的子载波传输数据，具有高的频谱效率。OFDM系统通过在每个符号的前面添加循环前缀，可以降低多径效应对信号的影响，对抗频率选择性衰落。同时，OFDM技术还可以与空时编码和分集等技术相结合，提高系统的通信质量。

Ke Guan在现实条件下评估了LTE的性能，通过使用一个混合的高铁信道模型，其中包括WINNER II信道模型，3GPP高速列车信道模型和基于郑州-西安客运专线大尺度模型[4]。Yeh C Y通过实现对发射机和接收机本振的绝对同步，来达到检测每条路径绝对时延的目的，文中使用了基于OFDM的检测系统，并将其用于台湾高铁信道环境的检测中[5]。Uche A K等人研究了车间（V2V）通信系统，由于发射终端和接收终端的移动性，并且动态散射体的存在，因此车间（V2V）通信信道是非平稳的，给出了Non-WSSUS信道的时间尺度域特性和统计特性[6]。本文给出了高速铁路环境中的信道建模，并通过对比一些常用的信道估计方法，推导得到了WSSUS（Wide-Sense Stationary with Uncorrelated Scattering）信道和Non-WSSUS信道模型，实验结果表明：基于Non-WSSUS的信道模型，在OFDM系统中，探索了在不同时速、天线配置、插值方法和调制方式，对系统性能的影响。

1 OFDM系统

OFDM系统将高速的数据流通过串并转换，变为符号长度增加的低速并行数据流，并将它们调制到相互正交的子载波上传输，通过在每个OFDM符号之间添加长度大于信道最大时延扩展的保护间隔，可以最大限度的消除符号间干扰，如果保护间隔是OFDM符号的尾部部分，也能确保子载波之间的正交性。由于这些子载波是相互正交的，因此可以最大限度的利用频谱资源，OFDM系统的原理框图如图1所示[7]。

图1 OFDM系统的原理框

在发射端，对于第n个OFDM符号的时域表达式为：

其中，K为子载波数，k为子载波序号，m为调制符号序号，X为频域发射信号。

接收端收到的信号可以表示为发送信号和信道冲激响应的线性卷积：

其中，L为信道的最大时延扩展，N和Ng分别为OFDM符号的子载波数和保护间隔的采样数，w[n,m]为高斯白噪声。

接收信号的频域表达式可以写为：

其中，H表示信道频域响应，X为频域发射信号，W为频域噪声。

2 高速铁路中的无线信道建模

对于非直射径的高速铁路场景中的无线信道模型如图2所示[8-9]，本文将模型简化为只考虑接收天线的运动。

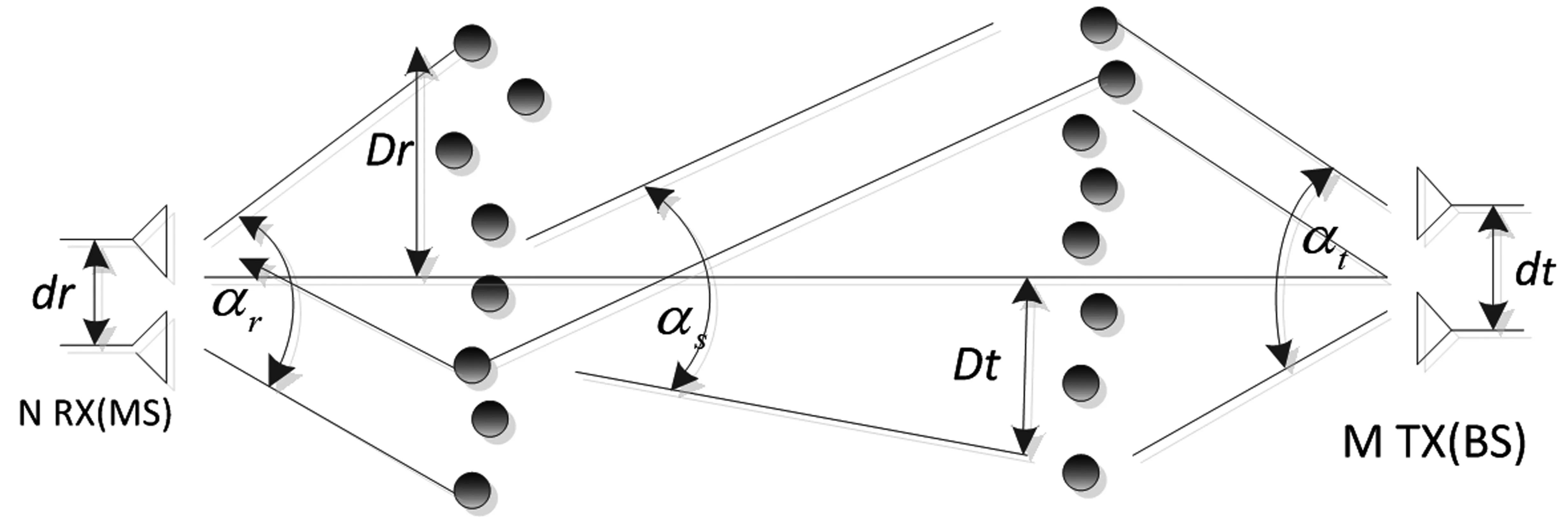
图2 高速铁路场景中的无线信道模型

假设在基站和移动台附近都存在S个散射体，散射半径分别为Dt和Dr，这些散射体被认为是全方位理想的反射来波信号，基站附近的散射体捕获基站的信号，并将其以平面波的形式发射到移动台附近的散射体。

将散射体近似考虑为线性阵列的形式，间距为2Dr/S，因此，移动台附近的散射体接收的信号为：

其中，Gt=[g1g2… gM]是S×M的信道矩阵，R描述散射体捕获的信号之间相关性，考虑到发射天线之间的相关性，上式改写为：

移动台天线接收到的信号为：

其中，Gr是N×S的信道矩阵，R描述接收天线之间相关性。进一步定义等效信道的频域形式为：

2.1 WSSUS信道

WSSUS信道是大多数信道建模的出发点。本文用h(t;τ)表示信道的等效低通冲击响应。在广义平稳非相关散射信道的条件假设下，有两层含义：广义平稳和非相关。首先来看第一层假设-广义平稳，需要满足：h(t;τ)的均值与t无关和自相关函数只与时间间隔Δt有关，即自相关函数可以表示为：

其中，Rh(Δt;τ)称为信道的平均功率输出。从式（8）可以理解为：广义平稳信道的二阶统计量是不随时间变化的，瞬态信道还是随时间变化的。第二层假设-非相关，不同延迟的分布是不相关的。基于上述两层假设，时变WSSUS信道的冲击响应可近似表示为：

其中，φn，τn和vn分别表示第n条路径的随机相位（[0,2π]的均匀分布）、时延和多普勒频率。L为路径的条数，其数值越大，表示的模型越为精准，一般情况下，取值7左右的整数即可。

2.2 Non-WSSUS信道

WSSUS的假设能够大大简化线性时变（Linear Time-Varying，LTV）信道的统计特性[11]。但是，在实际的无线信道中，只在一定的时间段和频率段中满足这种假设条件。WSSUS信道的一个基本属性是不同的散射体（延时-多普勒分量）是不相关的，并且扩展函数是白过程。实际上，这种特性并不能满足，因为信道分量在延时-多普勒域中彼此非常接近，导致了相同的物理散射体，因此这些散射体是相关的。另外，在发射端或者接收端的滤波器、天线和加窗都可以被认为是信道的一部分，它们会引起额外的时间和频率弥散，这将导致整个信道中的扩散函数的相关性。对Non-WSSUS信道的另一种观点建立在时频变换函数上，它将不再是时频域平稳的[12]。引起时频变换函数非平稳性的物理机制包括阴影、延时和多普勒频移，这些机制往往都是由移动性和传输环境的改变所带来的。它们一般发射在大尺度范围，而不是小尺度衰落。Matz提出用本地散射函数（Local Scattering Function，LSF）来作为信道物理意义上的二阶统计特性，它将WSSUS信道的散射函数扩展到Non-WSSUS信道中[13]。本地散射函数定义为时频变换函数或者扩展函数的四维相关函数的二维傅立叶变换。作为描述信道统计特性的本地散射函数展现的是信道的非平稳性。由此可以得到Non-WSSUS信道的近似表达式为：

其中，αn，τn和vn分别表示第n条路径的衰减系数，时延（范围为[0,τmax]）和多普勒频率（范围为[0,vmax]）。

3 OFDM信道估计

对基于OFDM系统的信道估计方法一般可以分为两大类：盲信道估计和非盲信道估计。盲信道估计方法研究接收信号的统计信息，这个过程需要大量的接收数据。但是，对于快衰落信道，盲信道估计的方法性能会下降很多。另一方面，在非盲信道估计中，接收端需要知道先验的信道信息或者部分发射信号来进行信道估计。对于非盲信道估计方法的研究主要基于两个方向：辅助数据和判决指导。其中，辅助数据的方法应用范围较广。在辅助数据的信道估计中，接收端是已知一个OFDM符号完整数据或者部分数据，这样可以很容易的估计信道信息。经常用到的辅助数据就是插入导频，导频分为块状导频和梳状导频，考虑到本文所研究的高铁信道的快衰落特性，必须采用梳状导频来跟踪信道。

假定OFDM符号间隔为T和带宽为W，则最大可分辨的延迟和最大可分辨的多普勒偏移分别表示为：

则式（10）中的衰减系数αn的矩阵形式可以表示为：

为了方便将应用时-频双选择信道，将式（10）进一步近似为：

离散化后，可得：

其中，T0∈ [τmax,1/vmax]和 W0∈ [vmax,1/τmax]。

最后将式（15）带入到式（3）中，采用LS、MMSE等一系列算法即可进行信道估计。

4 实验仿真

参考3GPP TR 25.996 Version 7.0.0 Release 7参数设置对高速铁路的信道估计进行仿真，载波频率为2 GHz，λ为波长基站的天线间距为2.5 m，移动台的天线间距0.5λ，基站附近和移动台附近的散射体数目分别为10和20。发射端和接收端均采用OFDM系统，子载波总数为128，CP长度为16，由于高铁信道是时变的，本文采用梳状导频，导频间隔为5，由于LS方法比LMMSE方法实用性高且算法复杂度低，可以有效降低高速铁路通信传输时延，文中的信道估计均采用LS方法。

首先，本文探索了列车在不同运行速度条件下信道估计。仿真条件为单发单收天线信号调制方式是16QAM，插值方法是线性插值。从图3可以看出，列车的运行速度越快时，相同信噪比下的误码率越高。这是由于列车速度越高，所引起的多普勒频移越大引起信号失真。

图3 不同运行速度下信道估计结果

同时，本文进一步分析了不同的天线单元配置下的高铁信道估计。基于图3的分析结果，列车的运行速度设为250 km/h，其余仿真条件不变。如图4所示，可见发射天线数目的增加会使得接收端误码率有所降低。

图4 不同天线配置下信道估计结果

为了分析插值方法对高铁信道估计的影响，图5分析了三种插值方案对系统BER性能的影响。设列车的运行速度为250 km/h，天线配置为单发单收，采用16QAM信号调制方式，三种插值方法分别为线性插值、二阶插值和三次样条插值方法，从图5可以看出在这种高铁信道模型中它们的插值效果并没有显著的区别。

最后，本文分析了不同信号调制方式对高铁信道估计的影响。天线配置设为单发单收，插值方法为线性插值，在250 km/h和350 km/h两种速度下，分别采用16QAM和QPSK两种调制格式。如图6所示，可见列车在相同的运行速度条件下，采用QPSK会比16QAM具有较低的误码率。

图5 不同插值方法的信道估计结果

图6 不同信号调制方式下信道估计结果

5 结 语

本文给出了高速铁路环境中的信道建模，并通过对比一些常用的信道估计方法，推导得到了WSSUS信道和Non-WSSUS信道模型。在此基础上，推导了OFDM系统下的等效信道矩阵的表达方式。最后在实验仿真部分，基于Non-WSSUS的信道模型，在OFDM系统中，探索了在不同时速、天线配置、插值方法和调制方式，对系统性能的影响。