基于二进制编码多导频搜索的导频设计
2022-02-18黄海燕朱俊杰郑志安何明芳刘健健
黄海燕,朱俊杰,郑志安,何明芳,刘健健
(中南林业科技大学 计算机与信息工程学院,长沙 410004)
0 引 言
正交频分复用 (Orthogonal Frequency Division Multiplexing ,OFDM) 技术作为无线通信的核心技术,能够有效抵抗无线通信传输的多径效应。而在OFDM系统中,信道估计十分必要,传统算法常常使用最小均方误差(Minimum Mean Square Error, MMSE)和最小二乘误差(Least Square, LS)[1]作为信道估计算法,导频开销较大。近年来,压缩感知(Compressive Sensing, CS)在信道估计中的应用考虑了信道的系统特性,不仅提高了系统性能,还降低了导频开销,提高了频谱利用率。
CS理论中[2],测量矩阵的构造必须满足有限等距性质(Restricted Isometry Property, RIP),但在应用中无法实现。而文献[3-7]提出了利用信道数据MMSE和最小互相干性(Minimum Mutual Property,MIP)的测量矩阵设计方案,由于MIP易于实现,方便检验,故本文主要是利用MIP作为优化导频的目标函数。虽然穷举法可以找到最优导频,但其占用大量内存且有较高的计算复杂度,不具有实用性。文献[8]通过数学推导出满足循环差分集(Cyclic Difference Set,CDS)导频集的MIP最小,但并非所有的载波与导频集都有CDS,因此文献[6]提出了一种基于离散随机逼近 (Discrete Stochastic Approximation, DSA) 算法来寻找导频集,但当子载波数目较大时,搜索空间会增大;文献[9]提出了一种具有内外循环的随机顺序搜索(Stochastic Sequential Search,SSS)方法,其通过内外循环迭代寻找最优导频集合,但 SSS方法需要更多的计算复杂度和更长的时间,且子载波数量越大,时间复杂度呈指数增长;文献[10]提出了基于遗传算法的导频设计算法,但该算法需要的交叉和变异概率需要不断验证,否则算法容易局部收敛;文献[11]基于尾迭代串联CDS的方法寻找导频,但该方法找到的MIP并非最小。现有文献[12-16]中的算法都是从全子载波中选择导频集,在实际应用中,并非所有的子载波都放置了数据,因此从实际出发,本文考虑有限带宽范围的导频集合。
本文提出了一种基于二进制编码的多导频并行搜索导频优化算法,该算法将导频集合进行了二进制编码,利用MIP准则进行导频更新。更新导频首次采用多个导频同时更新,增加了导频组的多样性,为下次迭代提供了更多可能性。实验结果表明,该算法能找到较优的导频集合,是可以提高信道估计性能的优化试验模型。
1 系统模型
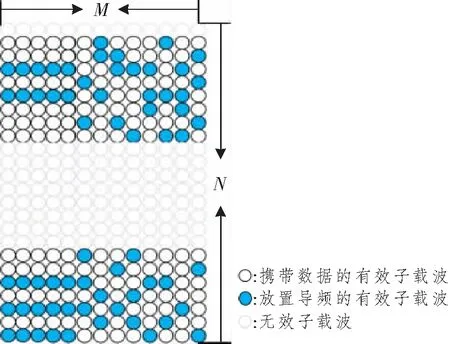
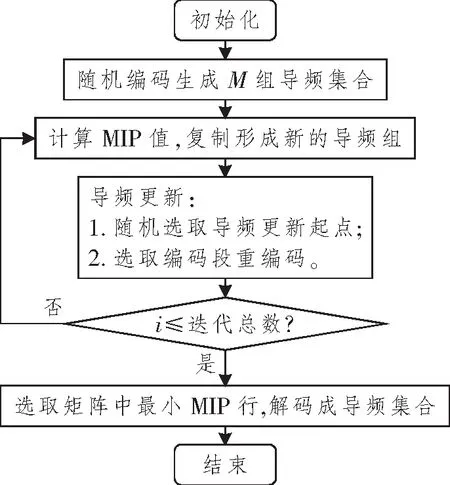
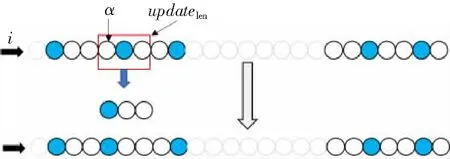
我们考虑N个子载波的OFDM系统,其中Nc和Np分别为有效子载波和导频。在有效子载波范围内,一组导频P={p1,…,pNp}⊆Nc⊆(1 式中:k为虚数;τL为时延集合;T为OFDM符号长度。考虑到信道固有的系数信道冲击响应,信道估计技术能够利用较少的导频得到准确的信道估计。本文利用测量矩阵的MIP作为选取导频集合的目标函数,MIP为矩阵F任意两列的最大内积,如下所示[10]: 式中,fm和fn分别为矩阵F第m与第n列的值。 本文没有考虑到导频符号的能量,所以式(3)可以写成: 导频优化的最终目的就是找到MIP。其目标函数为 则最优导频位置popt可表示为 图1 导频排列示意图 对导频位置进行二进制编码后,导频优化的目标函数Q0变为 式中:s为所有导频可能的搜索组合;p为每个OFDM符号的导频组合。 对一个OFDM符号按式(7)进行二进制编码,其中任意连续两个及两个以上的编码统称为编码段。图2所示为一个OFDM符号的二进制编码示意图。 图2 一个OFDM符号的二进制编码图示 本文算法流程图如图3所示。 图3 算法流程图 算法的具体步骤如下: (1) 初始化; (2) 随机编码生成M组导频集合: 式中:P为一个二进制矩阵;i为接下来的迭代次数。 (3) 将式(5)作为目标函数,计算式(9)矩阵每一行的MIP值,选择具有较小MIP的K行,复制M/K次形成一个如式(9)初始尺寸规格的矩阵,其中M能被K整除,M/K的大小取决于想要的矩阵大小,本文一般取3~6之间。 (4) 更新导频位置,导频更新规则为 式中:Pi为一个OFDM符号的编码位置,也就是导频位置;updatelen和α分别为编码更新长度和起点。找到更新起点并更新编码段,然后更新导频。图4所示为对更新起点为α和编码段长度为updatelen的导频进行随机编码更新的规则示例图,其准则是该编码段导频数量不变,只是随机更新其导频位置。 图4 导频更新的规则示例 然而,导频更新有一些特殊的情况,可以总结如下:当更新起点正好是在无效子载波起点往前一个更新长度updatelen的任意一点时,则导频更新可表示为 更新导频只在式中对应的OFDM符号位置选中导频,再将其更新替换为新的导频组。 同理,当选中的编码段正好与载波后半部分长度一致时,则导频更新的原则为 即只在该更新编码段开始寻找任意的编码段,并将原始编码段替换为该编码段更新后的导频位置,变成新的导频更新组。 (5) 重复步骤(3),直到算法迭代次数结束,找到MIP的二进制编码。 (6) 解码找到导频集合,算法结束。 为了验证算法的有效性,在本节中使用所提算法和DSA[8]算法来寻找最优的确定性导频模式,并且比较所提算法与现有方案DSA[8]算法的性能,实验采用正交幅度调制(Quadrature Amplitude Modulation,QAM)。表1所示为OFDM系统的仿真参数。 表1 OFDM 系统的仿真参数 图5所示为本文所提算法和DSA算法的MIP收敛速度曲线图。我们给出了两组对比图,算法每次仿真都保证在相同的搜索空间中。由图可知,无论子载波的数量为512还是1 024,本文所提算法都能够比DSA算法收敛的更快,且能够找到更小的MIP矩阵,说明本文所提算法性能较好。 图5 不同算法的收敛比较 图6所示为本文所提算法和DSA算法的误码率性能随信噪比的变化曲线。由图可知,当子载波数为512时,本文所提算法误码率性能明显优于DSA算法。当子载波数为1 024时,本文所提算法在信噪比较小时一直优于DSA算法,而在信噪比较大时,本文所提算法与DSA算法的误码率几乎相等。导频的开销越大,性能相对越差,该性能差异是由比较的子载波个数不同导致的。 图6 本文算法与DSA算法的误码率比较 表2给出了本文所提算法和DSA算法在提出的无效子载波条件下找到的最小MIP导频集合。由表可知,本文所提算法的g(p)值小于DSA算法,给出的导频集合可方便读者验证导频数据的真实性。 表2 DSA与本文所提算法的导频集合 本文研究了有效子载波范围内稀疏信道的导频优化算法。与现有方法相比,本文将多个导频进行并行搜索,而不是单一的迭代导频,由此增加了导频组合的多样性。实验结果表明,与现有方法相比,本文所提方法具有更小的MIP,且优化后的导频模型具有更好的稀疏信道估计性能。然而,在有效载波选择导频的情况下,本文对MIP的下界还没有理论验证。
2 导频图样设计算法
2.1 导频的二进制编码
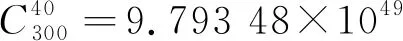
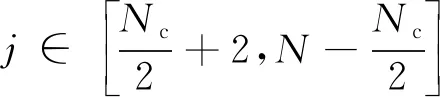
2.2 编码段

2.3 算法步骤

3 系统仿真




4 结束语
