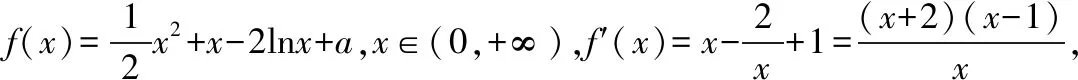浅谈“数形结合法”解决方程根的分布问题

陕西 张晓莹

方程根的分布问题一直是高考中重点考查的一类题型，这类题型经常与函数等相关知识综合考查，借助多个函数图象数形结合，将抽象的数学语言转化为直观的几何图形来观察方程根的情况，即数形结合将根的分布问题转化为函数的零点问题或者多个函数的交点分布问题.如果能发现试题规律，掌握做题技巧，那就可以得到事半功倍的效果.下面笔者结合几道例题谈谈如何巧用数形结合思想解决方程根的分布问题.

题目1：已知关于x的一元二次方程x2+2mx+2m+1=0.

(1)若方程有两个根，其中一个根在区间(-1,0)内，另一个根在区间(1,2)内，求m的取值范围；

(2)若方程的两个根均在区间(0,1)内，求m的取值范围.

思路1：数形结合将方程根的分布问题转化为二次函数的零点分布问题

(1)分析：方程x2+2mx+2m+1=0的两个根，一个根在区间(-1,0)内，另一个根在区间(1,2)内，可以转化为二次函数f(x)=x2+2mx+2m+1的零点一个在区间(-1,0)内，另一个在区间(1,2)内，根据二次函数的图象，只需求解f(-1)>0,f(0)<0,f(1)<0,f(2)>0不等式组即可.

解法：令f(x)=x2+2mx+2m+1，因为f(x)=0的一个根在区间(-1,0)内，另一个根在区间(1,2)内，所以函数y=f(x)有两个零点，一个在区间(-1,0)内，另一个在区间(1,2)内，

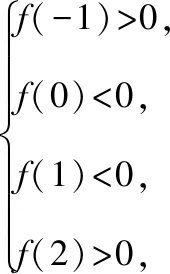
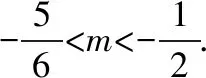
点评：将方程根的分布转化成函数零点的分布，只需根据函数图象讨论区间端点的函数值应满足的不等关系即可.

.

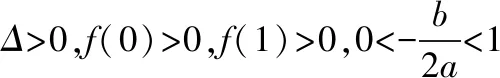
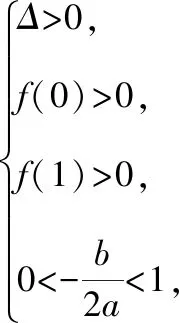
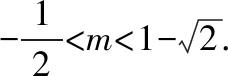
点评：根据二次函数的图象，讨论区间端点函数值的正负.另外，必须根据图象讨论Δ的值及对称轴的位置.

思路2：转化为抛物线与直线交点的分布问题

(1)分析：方程根的分布可以转化为二次函数f(x)=x2与一次函数g(x)=-2m(x+1)-1的交点分布问题，又g(x)恒过点P(-1,-1)，根据图象可分析出动直线g(x)只能从PA转到PB，写出直线g(x)斜率的取值范围.

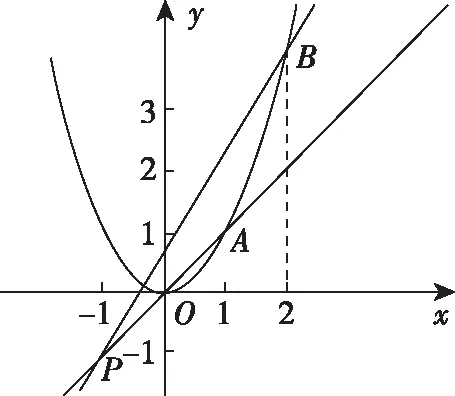
点评：根据方程的特点，方程根的分布可以转化为两个函数的交点问题，二次函数f(x)的图象可直接画出，直线g(x)是恒过定点P(-1,-1)的动直线，通过转动直线，找到与抛物线两个交点的横坐标分别在区间(-1,0)和区间(1,2)内，得到直线斜率应该满足的条件.

(2)分析：根据图象分析出动直线g(x)只能从PB转到PA，写出g(x)斜率的取值范围.又PB为f(x)=x2的切线，所以需要求出f(x)的导函数得到点B的坐标.

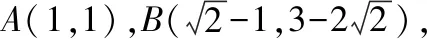
点评：问题的关键是分析出g(x)斜率的取值范围，并求出PB和PA的斜率值.

思路3：转化成对钩函数与常函数对应图象交点的分布问题

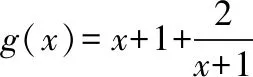
点评：问题的关键是画出y=g(x)的函数图象，并能观察出两函数图象交点的横坐标分别在区间(-1,0)和区间(1,2)内时m的取值范围.

(2)分析：画出g(x)的图象，观察其与直线f(x)=2-2m的交点分布情况，得到yA<2-2m

点评：问题的关键是画出函数y=g(x)的图象，并能观察出两函数图象交点的横坐标在(0,1)上时m的取值范围.

点评：利用两个函数图象的特点，分析如何建立等价的不等关系.

分析：由题设条件，利用导数性质推导出f(x)在区间(0,1)上单调递减，在区间(1,+∞)上单调递增，要使f(x)在区间(0,2)上恰有一个零点，只需f(1)=0或f(2)≤0，由此可求出a的取值范围.

点评：利用导数性质推导出f(x)的单调性，结合图象得出不等关系.