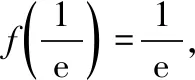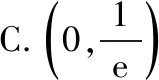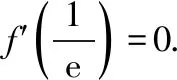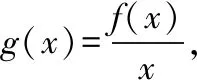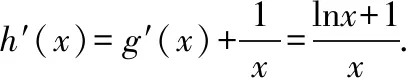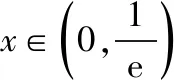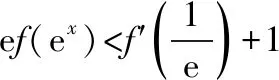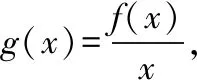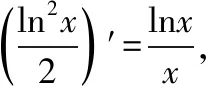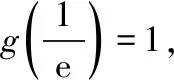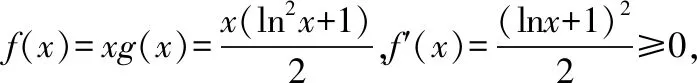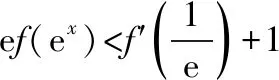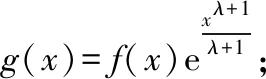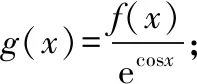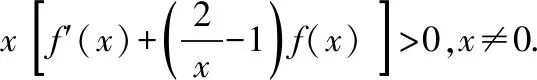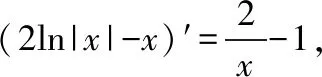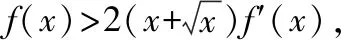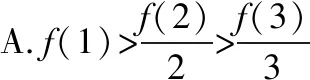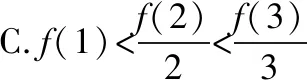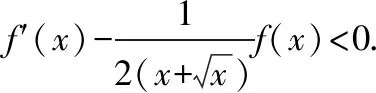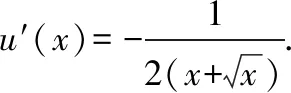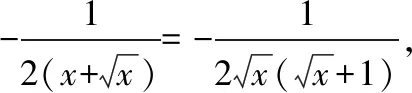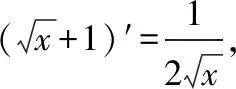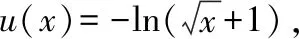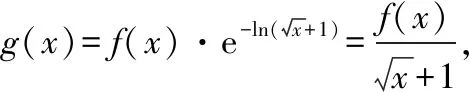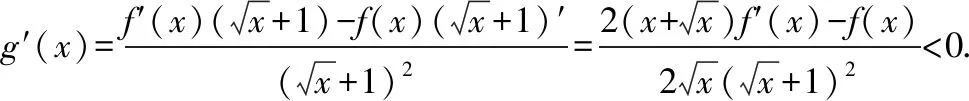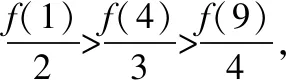构造函数解决一类与导数有关的不等式问题

广东 邓启龙

导数和不等式是高考复习中的重点和难点,而这两类问题的结合使得问题变得复杂、灵活.如何把握这一类问题的本质,研究它们的通法,是教师迫切关心的问题.下面将从一个高考经典题目出发,去探索此类与导数有关的不等式问题.

【例题】(2015·全国卷Ⅱ·理12)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是

( )

A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)

C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)

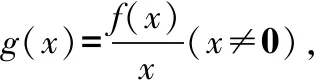
因为当x>0时,xf′(x)-f(x)<0,所以g′(x)<0,故g(x)在(0，+∞)上单调递减.

因为f(x)是奇函数,所以g(x)是偶函数,故g(x)在(-∞,0)上单调递增,且有g(-1)=g(1)=0.

当00,则f(x)>0；当x<-1时,g(x)<0,则f(x)>0.

综上所述,使得f(x)>0成立的x的取值范围是(-∞,-1)∪(0,1),故选A.

【探究】解决本题的关键在于从函数及其导数满足的条件出发,重新构造函数,然后利用新函数的单调性求解.

对于构造函数解决此类与导数有关的不等式问题,常见的构造如下：

(1)对于xf′(x)+λf(x)>0(其中λ为常数),构造g(x)=xλf(x)；

(2)对于f′(x)+λf(x)>0(其中λ为常数),构造g(x)=f(x)eλx；

(3)对于sinx·f′(x)+cosx·f(x)>0,构造g(x)=f(x)·sinx；

(4)对于cosx·f′(x)-sinx·f(x)>0,构造g(x)=f(x)·cosx.

下面结合两个例题说明如何构造函数.

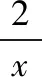
例1.函数f(x)是定义在R上的奇函数,对任意x∈R有2 016f(-x)

( )

A.f(2 016)<0 B.f(2 016)

C.f(2)<0 D.f(2)>e-4032

【解析】由已知可得f(0)=0,且对任意x∈R，有f′(x)+2 016f(x)>0.

构造函数g(x)=f(x)e2016x,则g′(x)=e2016x[f′(x)+2 016f(x)]>0,故g(x)在R上单调递增,且g(0)=0,g(1)=f(1)e2016=1.

因为g(2 016)>g(1),所以f(2 016)>e-20162,故选项A,B都错误.

因为g(2)>g(1),所以f(2)>e-4032,故选D.

( )

A.(-∞,-1) B.(-1,+∞)

从以上例子可以看出,遇到常见的与导数有关的不等式条件,通过构造对应的函数,利用单调性可以解决问题.如果遇到未见过的不等式条件,如何快速构造出对应的函数？通过探索,笔者发现很多与导数有关的不等式条件都可以转化为f′(x)+λ(x)f(x)>0(或<0),而对于f′(x)+λ(x)f(x)>0(或<0),构造函数g(x)=f(x)eu(x)即可,其中u(x)满足u′(x)=λ(x).原理如下：g′(x)=f′(x)eu(x)+f(x)eu(x)u′(x)=eu(x)[f′(x)+u′(x)f(x)],因为u′(x)=λ(x),所以g′(x)=eu(x)[f′(x)+λ(x)f(x)]>0(或<0),然后利用函数g(x)的单调性解决问题.于是找到了解决此类与导数有关的不等式问题的通法.

利用此通法,给出以下构造：

(7)对于f′(x)+cosx·f(x)>0,构造g(x)=f(x)esinx.

下面通过两道难度较大的例题来说明如何利用通法来构造对应的函数.

例3.定义在R上的函数f(x)满足(2-x)f(x)+xf′(x)>0,则f(x)

( )

A.恒大于等于0 B.恒小于0

C.恒大于0 D.恒小于等于0

因为当x<0时,g′(x)<0,当x>0时,g′(x)>0,所以g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,于是任意x≠0,g(x)>g(0)=0,所以任意x≠0,f(x)>0.

又因为f(0)>0,所以f(x)恒大于0,故选C.

( )

构造函数g(x)=f(x)eu(x),

所以g(x)在(0,+∞)上单调递减.