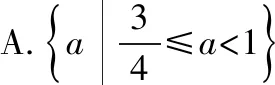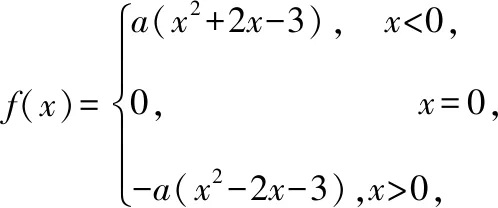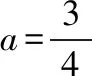追本溯源,突破难点
——二轮复习中的“一法”解“嵌套函数的零点问题”
2019-04-24安徽乔天恩
安徽 张 威 乔天恩
高三二轮复习是承上启下的阶段,是促进知识系统化、条理化及灵活运用的关键时期,更是促进学生能力发展的关键时期.二轮复习主要是对各个专题知识进行系统整理,形成知识网络,完善认知结构,使学生掌握各个专题的主要应用题型,归纳总结解题规律与方法,查漏补缺,解决在各个专题中学生存在的疑难问题,运用所学知识对主要题型举一反三、延伸拓展,提高学生分析问题与解决问题的能力.教师需要选择合适的切入点,引导学生从“题海”中解脱.针对这种教学要求,教师可以采用“一题多解”与“多题一解”的教学方式,帮助学生逐步地提升思维能力,掌握解题技能.下面笔者通过“多题一解”的教学方式,来突破 “求函数f(g(x))或函数af2(x)+bf(x)+c的零点问题”这个难点.暂称这类函数为 “嵌套函数”. “嵌套函数”的零点问题是很多学生都难以跨越的“一道鸿沟”.那么该如何跨越这道“鸿沟”呢?具体如下.
一、典例分析——突破重难点

1.【命题维度分析】
【考点】本题考查分段函数、二次函数的图象和性质、函数的零点等知识.
【核心素养】本题考查逻辑推理、数学建模、数学运算、直观想象核心素养.
【数学能力】本题考查空间想象能力、抽象概括能力、推理论证能力、运算求解能力.
2.【解题维度分析】
【思想方法】本题考查函数与方程思想、数形结合思想、分类讨论思想、转化与化归思想.
【解题分析】本题已知函数解析式和函数零点个数,求解参数a的取值范围.求解函数零点的问题,有以下求解函数零点问题的几种基本原理:第一,通过直接解关于x的方程f(g(x))=0进行求解;第二,通过画出函数f(g(x))的图象,并判断该函数的图象与x轴的交点个数进行求解;第三,将方程f(g(x))=0构造成h(x)=u(x)形式,即转化为函数h(x),u(x)的图象交点个数进行求解;第四,利用零点存在性定理进行求解.而本题很难直接采用上述几种原理进行求解,原因是函数f(g(x))是一个“嵌套函数”,其解析式求解起来比较繁琐,同时该函数的图象不易得到.那么该如何解决这个“嵌套函数”呢?可以进行换元,令t=g(x),设f(t)=0的实根为ti(i=1,2,…),则“f(g(x))=0的实根个数”等价于“直线y=ti与函数g(x)的图象的交点个数”或“关于x的方程ti=g(x)的实根个数”.可以发现通过转化与化归后,原题就回归到熟知的函数零点问题的类型了.具体过程如下.
【解析】令t=g(x),则f(g(x))=0,即转化为f(t)=0,
先求f(t)=0,再解方程t=g(x),得到的x即为函数f(g(x))的零点.
(Ⅰ)当t<0时,令ln(-t)=0,得t=-1,
①当a>1即-1>1-2a时,t=g(x)有2个实根;
②当a=1时,t=g(x)有1个实根;
③当a<1时,t=g(x)有0个实根;

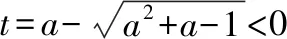
此时t=g(x)有2个实根,结合①,可知y=f(g(x))有4个零点;
(2)当a=1时,t=0或2,则t=g(x)有4个实根,结合②,可知y=f(g(x))有5个零点,与题意不符;

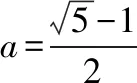
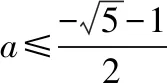
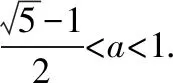
【例2】已知函数f(x)=x2ex,若函数g(x)=f2(x)-kf(x)+1恰有4个零点,则实数k的取值范围是
( )

1.【命题维度分析】略
2.【解题维度分析】
【思想方法】略
【解题分析】本题看起来和例1是属于两种不同类型的函数零点问题,其实两个题如出一辙.只需要对原题进行稍许改变,即可转化为例1的形式.如下,
令h(x)=x2-kx+1,则函数g(x)=f2(x)-kf(x)+1恰有4个零点,即转化为函数h(f(x))恰有4个零点.此时即可利用例1的解题原理进行求解.具体过程如下,

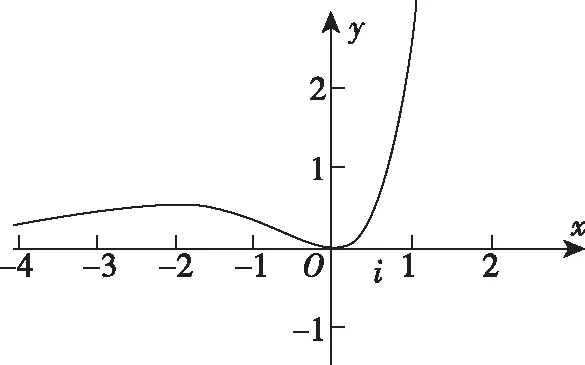
令t=f(x),因为关于t的方程t2-kt+1=0至多有2个实根,
①当Δ<0时,g(x)显然无零点,此时不满足条件;
②当Δ=0时,t2-kt+1=0有且只有一个实根,
由f(x)的图象可得t=f(x)至多有3个实根,所以g(x)至多有3个零点,故不满足条件;
③当Δ>0时,即k2-4>0,则k<-2或k>2,
此时t2-kt+1=0有两不等根t1,t2,设t1 且t1+t2=k,t1·t2=1,若g(x)有4个零点, 1.解题原理:通过对上述的两个例题的分析,可以发现无论是解决形如f(g(x))的函数零点问题,还是形如af2(x)+bf(x)+c的函数零点问题,其解题原理基本一致,都是通过换元思想和整体代换思想进行求解,具体解题步骤,可以归纳如下. ①换元,令t=g(x)(t=f(x)); ②求解函数f(t)(g(t))的零点或零点个数; ③求解方程t=g(x)(t=f(x))的实根或实根个数或通过已知零点个数判断参数的取值范围. 这种方法的实质是将函数f(g(x))或af2(x)+bf(x)+c的函数零点问题拆分成②③两个问题进行求解. 2.易错点:①没有理解函数f(x)与f(t)是同一个函数;②函数f(x)的图象画错;③误将t的个数当作f(g(x))或af2(x)+bf(x)+c的函数零点个数;④数形结合时,考虑不完善. 变式教学是对有关数学概念、定理、通性通法等进行不同角度、不同层次、不同背景的变化,有意识地引导学生从“变”的现象中发现“不变”的本质,从“不变”中探求规律,从而达到对知识、方法等熟练掌握和灵活运用. 变式教学是为了将本源知识进行进一步巩固和延伸拓展.针对例1,例2,笔者设置了如下两个变式题,对此种类型的题目的解题原理进一步巩固,从而突破这个在高考中的难点问题.具体如下. 【变式1】已知f(x)是定义在R上的奇函数,当x<0时,f(x)=a(x2+2x-3),其中a>0,若函数y=f(f(x))恰有7个零点,则a的取值范围是 ( ) 【答案】D 【解析】此题与例1相比嵌套的函数不同,同时函数f(x)的解析式需要通过奇函数的性质求解,当f(x)的解析式求解出来时,下面的解法与例1基本一致.具体解法如下. ①换元:令t=f(x); ②求解f(t)的零点:可得t=-3或t=0或t=3; 【变式2】已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若f(x1)=x1,且x1 ( ) A.3 B.4 C.5 D.6 【答案】A 【解析】此题与例2相比嵌套的函数是一个三次函数,同时关联了该函数的极值点问题,由已知可得x1,x2是方程3x2+2ax+b=0的两根,由f(x1)=x1,且x1 ①换元:令t=f(x); ②求解f(t)的零点个数:可得t=x1或t=x2; ③求解方程t=f(x)的实根或实根个数:即f(x)=x1和f(x)=x2,因为f(x1)=x1
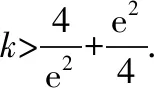
二、题后反思——总结解题原理和易错点
三、精彩变式——巩固解题原理