一种基于邻居节点和边的复杂网络节点排序方法——NL中心性算法
2019-04-19刘书磊杜家乐邵增珍
刘书磊,杜家乐,邵增珍,3*
(1.山东师范大学,山东 济南 250014;2.济南市历城一中,山东 济南 250115;3.山东女子学院,山东 济南 250002)
根据节点的影响力对节点排序是当前研究热点之一,可应用于多个领域,如在有影响力个体的协助下提高信息在社交网络中的传播速度[1-2]、查找重要节点以避免级联故障[3]、控制流行病的传播[4]等。衡量节点影响力的关键是如何评估节点的传播能力。
国内外学者对节点传播能力的评估进行了大量研究,目前常用的方法有度中心性[5]、介数中心性[6]、紧密度中心性[7]、局部中心性[8]和k-核分解法[9]等。度中心性是最简单的一种评估方法,该方法认为节点的传播能力与其它连接的节点个数有关,即节点的邻居节点越多,其传播能力越强。该方法虽然简单直观,但只考虑了节点的局部属性,因此具有一定的局限性。介数中心性和紧密度中心性是一种全局属性,因其时间复杂度较大,所以这两种方法都不能应用到大型的复杂网络中。考虑到局部属性缺乏准确性,而全局属性的计算时间又较长,Chen等[8]提出了一种折中策略——局部中心性,该方法使用多层邻居节点的个数描述节点的重要性,同时考虑计算时间和节点周围的局部属性。Kitsak等[9]发现越处于网络中心的节点,其传播效率越高。基于这种思想,提出了k-核分解法,但是k-核分解法会给传播能力不同的节点赋予相同的ks值,导致该方法对节点重要性的区别度太小。Zeng等[10]对k-核分解法进行了改进,提出了进一步区分节点度的MDD算法。Wang等[11-12]根据k-核分解法中节点的迭代次数进一步提高了节点的区分度。
虽然上述中心性方法从不同的角度对节点的重要性进行了计算,但这些方法都忽略了网络中另一个基本的元素:边。节点的重要性除了与本身的位置、邻居节点有关外,还应与其相连的边有关。Wang[13]等认为在网络中将边认为同等重要是不合理的,提出给边赋权值的思想,但他仍然依据节点的度对边进行区分,没有考虑边在网络中的重要性。Liu[14]认为边的重要性可以通过其连接能力和不可替代性来描述,并在此基础上提出了基于节点的度和连边重要性的DIL方法,该方法将边的重要性聚焦于其本身,从脱离节点的角度重新定义了边的权值,但是该方法在对节点进行排序时,只考虑了节点的度,而没有考虑节点的全局拓扑属性。
基于以上研究,本文对DIL方法进行了改进,提出了一种基于邻居节点和边重要性的节点排序方法——NL中心性算法,该方法从节点周围的局部结构和与其相连的边的重要性两个方面衡量节点的影响力。节点的局部结构被定义为以节点为中心,向外扩展3层邻居节点的子图结构。使用节点的局部结构不仅降低了计算复杂度,且更广泛地考虑了网络的全局拓扑属性。节点和边是复杂网络的两个基本属性,节点的影响力必然与其相连的边存在一定的关系。因此,本文在对节点的重要性进行排序时还考虑到了边对节点的影响。为了验证排序结果的准确性,将所提方法和其他中心性方法计算得到的排序结果与SIR传播模型得到的排序结果进行对比,结果表明无论是计算效率还是准确性,NL中心性算法都要优于其他中心性方法。
1 中心性方法简述
本文中提到的复杂网络均指无向并且边没有权值的复杂网络。定义G=(V,E)为复杂网络,其中V表示节点集合,n=|V|为节点个数,E为边的集合,m=|E|为边的条数。网络G的邻接矩阵定义为A={auv}∈Rn,n,若节点u和节点v直接相连,则auv=1,否则auv=0。
度中心性定义为一个节点的邻居节点的个数。一个节点的度越大,则说明该节点能够直接影响的邻居节点也就越多。用CD(v)表示节点v的度中心性,CD(v)定义为:
(1)
式中,Г(v)表示节点v的邻居节点集合,|Г(v)|表示集合Г(v)的大小。
节点v的紧密度中心性CC(v)是节点v到其余所有节点最短路径长度之和的倒数。节点的紧密度越大,则其与其他节点的连接越紧密,从而说明该节点在网络中所在的位置越重要。CC(v)定义为:
(2)
式中,duv表示节点u和节点v的最短路径长度,V/v表示除节点v之外其余节点集合。
局部中心性是介于度中心性和全局中心性的一种折中策略,不仅考虑了邻居节点,还考虑了次邻居节点,表示为CL(v)。若将节点v看做是第0层,局部中心性考虑了以节点v为中心,4层之内的所有节点的度。局部中心性越大,表示以节点v为中心的局部结构越庞大,从而节点v越重要。CL(v)定义如下:
(3)
式中,N(w)表示节点w邻居节点和次邻居节点的个数。
k-核分解法给每个节点标记一个整数或者说层数,表示节点的重要性程度。ks值越大说明节点越处于网络的中心,也就越重要;ks值越小说明节点越处于网络的边缘。k-核分解法一开始先删除网络中所有度为1的节点,这些节点删除后,若网络中出现了新的度为1的节点,则继续删除这些节点,直到网络中没有度小于等于1的节点,所有删除的这些节点的ks值为1。然后重复上述的步骤,直到网络中所有的节点都被赋值。
2 考虑邻居节点和边重要性的NL中心性算法
2.1 DIL及其存在的问题
DIL是一种较为新颖的中心性方法。在计算节点的影响力时,该算法不仅考虑了节点的度还考虑了边的重要性。首先定义边euv的重要性度量指标Ieuv:
(4)

(5)
DIL中心性将边的重要性加入到计算节点影响力的过程中,对节点的重要性具有较高的识别率,但DIL中心性在除去边的贡献值之外只考虑了节点的度,并未考虑全局拓扑属性对节点重要性的影响。以图1a、b两个简单网络为例,说明DIL中心性的缺陷。
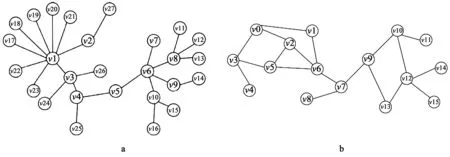
图1 简单网络Fig.1 Simple network
使用DIL中心性计算图1a中的节点重要性时,CDIL(v7)=CDIL(v11)=CDIL(v12)=CDIL(v13)=…=CDIL(v24)=CDIL(v27)=1,可以发现DIL中心性认为网络中所有度为1的节点的重要性相同。造成这种情况的原因是所有与度为1的节点相连的边不能和其他边组成三角形,因此边的重要性为0,从而使计算结果等于节点的度。也就是说,边的重要性为0时,DIL还是只考虑了节点的度,这就会造成使用DIL中心性对网络中节点进行排序时,所有度为1的节点的排序结果相等。从图1a中可以看出,v4节点连接了左右两个子图,那么与v4相连的节点v25也就比较重要,但是DIL中心性认为v25和其他度为1的节点同等重要,这显然是不合理的。
使用DIL中心性计算图1b中的节点重要性时,CDIL(v7)=7.4,CDIL(v10)=7.4,CDIL(v7)=CDIL(v10),说明节点v7和v10同等重要。但是从图1b的结构中可以看出,删除节点v7后,图1b被分割成3个子图:和节点v6相连的子图、和节点v9相连的子图和节点v8。删除节点v10后,图1b被分割成2个子图:节点v11和剩余节点组成的子图。删除节点v6后对图的连通性的破坏比删除节点v10后对图的连通性的破坏要大,说明节点v6比节点v10重要,这与DIL算法得到的结论相悖。综上所述,DIL中心性有两个缺陷:对网络中所有度为1的节点的排序结果相同,忽略了网络的全局拓扑属性,从而导致边对节点的贡献值相等时,排序结果完全依赖于节点的度。
2.2 NL中心性算法
针对以上问题,本文对DIL中心性进行了改进,提出一种基于邻居节点和边重要性(Neighbor nodes and importance of Lines)的计算方法——NL中心性(CNL(v))。CNL(v)具体定义如下:
(6)
公式(6)和公式(5)相比,NL中心性将DIL算法中节点的度替换为节点的局部结构,节点的局部结构是介于度中心性和全局中心性的一种折中策略,是以节点为中心向外扩展3层的子图结构。NL中心性认为,节点的重要性不仅与其相连的节点的个数有关,还应该与周围的拓扑结构有关,因此使用节点周围的子图表示节点的拓扑属性。使用节点的局部结构代替全局属性,不需要知道整个网络的结构,在减小时间复杂度的同时保证算法的准确性。
以图1b为例,计算v7节点和v10节点的重要性时,DIL中心性只考虑了节点的度,因为CD(v7)=CD(v10),v7节点和v10节点的边的重要性又恰巧相同,所以CDIL(v7)=CDIL(v10)。虽然节点v7和节点v10的度相同,但是与v7相连的v6相比于与v10相连的v12连接了更大的子图,所以v7节点更加重要。在使用NL中心性计算v7节点和v10节点的重要性时,因为考虑了以v7为中心的3层子图结构,所以节点v6的邻居节点和次邻居节点个数也在计算范围之内,从而对节点v7和节点v10的重要性做了进一步区分。具体计算结果为CNL(v7)=18.4,CNL(v10)=17.4,CNL(v7)>CNL(v10),与分析结果一致。再以图1a中节点v26和节点v27为例,CDIL(v26)=CDIL(v27)=1,CNL(v26)=18>CDIL(v27)=10,从而说明相比于DIL中心性,NL中心性能对节点重要性做出更加精确地区分。
使用DIL中心性计算节点重要性时,只考虑了节点的度和边的重要性,所以时间复杂度为O(n)。NL中心性在计算时,考虑了3层子图的节点的度,相比于DIL中心性,计算步骤只是成倍数增加而不是成指数增加,所以NL中心性的时间复杂度与DIL中心性的时间复杂度相等,仍为O(n)。
为了验证NL中心性的准确度,本文实验将NL中心性和其他已有中心性计算得到的排序结果和传播模型得到的排序结果进行比较,使用肯德尔相关系数描述排序结果的拟合程度,进一步比较所提方法的准确率。
3 实验
3.1 数据集
为了评价本文所提方法的准确性,把NL中心性应用到2个真实的复杂网络中。这2个真实的网络分别为:(1)海豚关系网络[15]。这是在新西兰神奇湾观察到的62只海豚的社团关系图。(2)单词邻接网络[16]。这是由19世纪英国作家查尔斯·狄更斯创作的小说《大卫·科波菲尔》中的普通名词和形容词邻接的无向网络,节点代表名词或形容词,边出现在相邻位置的两个单词。在实验过程中,以上2个真实网络均看作无向网络。
3.2 传播模型
在传染病动力学中,主要沿用由Kermack与McKendrick在1927年用动力学方法建立的SIR传染病模型[17]。在某一时刻,所有节点只能处于易感者(susceptibles)-染病者(infectives)-恢复者(recovered)3种状态之一。在SIR模型中,网络初始状态时只有一个节点处于染病者状态(I),其余所有节点处于易感者状态(S)。在传播过程中,一个病人能传染的易感者数目与此环境内易感者总数成正比,比例系数β也称为传播系数;从染病者中移出的人数与染病者数量成正比,比例系数为γ,论文中设置γ=1。单位时间内,易感者以概率β变为染病者,染病者以概率γ变为恢复者。一个节点的传播能力即为该节点在传播过程中可以感染的节点数。本文实验取100次传播过程的平均值作为节点的传播能力。
本文实验将SIR传播模型得到的排序结果与各中心性计算得到的排序结果进行比较,中心性方法计算得到的结果越接近于SIR传播模型得到的排序结果,说明该中心性方法的准确性越高。
3.3 评价指标
肯德尔相关系数[18]是一个用来测量两个随机变量相关性的统计值,并经常用希腊字母τ表示其值。肯德尔相关系数的取值范围在-1到1之间,当τ为1时,表示2个随机变量拥有一致的等级相关性;当τ为-1时,表示2个随机变量拥有完全相反的等级相关性;当τ为0时,表示2个随机变量是相互独立的。
假设2个集合分别为X、Y,其元素个数均为N。2个集合取的第i(1≤i≤N)个值分别用xi、yi表示。X与Y中的对应元素组成一个元素对集合XY,其包含的元素为(xi,yi)。当集合XY中任意2个元素(xi,yi)与(xj,yj)的排行相同时(当xi>xj时yi>yj,或者当xi
肯德尔相关系数用于评价2个排序结果的相关程度,2个排序结果一个是通过SIR模型计算得到的结果,一个是通过中心性计算得到的排序结果。肯德尔相关系数越大说明中心性计算得到的排序结果越接近于传播模型得到的排序结果,从而说明中心性方法越准确。肯德尔相关系数定义如下:
(7)
式中,nc表示和谐对的个数,nd表示不和谐对的个数。使用肯德尔系数计算传播过程得到的排序结果和中心性计算得到的排序结果的相关性可以评价排序结果的准确性。
3.4 结果分析
在实验过程中使用CD表示度中心性,Ck表示k-核分解法,CC表示紧密度中心性,CL表示局部中心性,CDIL表示DIL中心性,CNL表示NL中心性算法。为了从减少传播系数对实验结果的影响, SIR传播模型中传播系数的取值设置为从0.01到0.2。将中心性计算得到的结果和通过传播模型得到的结果进行相关性比较,并计算肯德尔相关系数,实验结果如图2所示。
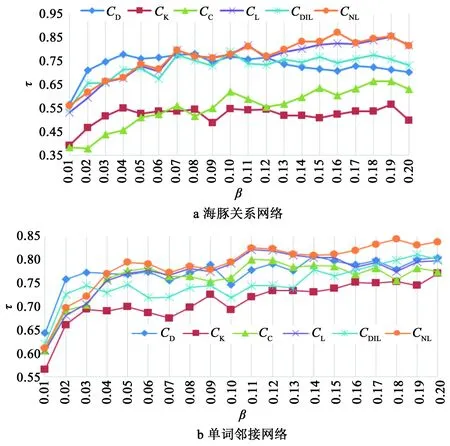
图2 排序结果相关性比较Fig.2 The correlation comparison of ranking results
图2a是将各中心性方法和传播模型应用到海豚关系网络中得到肯德尔相关系数,图2b是将各中心性方法和传播模型应用到单词邻接网络中得到的肯德尔相关系数,横坐标β表示传播系数,纵坐标τ表示肯德尔相关系数。
在图2a中可以看出,当传播系数小于0.07时,度中心性具有最高的准确性;当传播系数大于0.07时,NL中心性具有较高的准确性。造成这种情况的原因是当传播系数较小时,每个感染者节点只能以较小的概率感染易感染者,从而整个网络的传播效率较低,网络中被感染的节点数很少。度越大的节点越有更多的机会造成大的影响范围,因此当传播系数较小时,节点的影响力取决于其邻居节点的个数,也就是节点的度。因为DIL中心性在计算节点的重要性时也考虑了节点的度,所以在图2a中,传播系数小于0.05时,DIL中心性的排序结果要好于NL中心性;但是当传播系数大于0.05时,NL中心性的排序结果要好于DIL中心性。从图2a中也可以看出,当传播系数小于0.04时,度中心性具有最高的准确性;当传播系数小于0.03时,DIL中心性的排序结果要好于NL中心性。
图2a中,当传播系数大于0.07时,NL中心性的肯德尔相关系数最大。图2b中,当传播系数大于0.04时,NL中心性的肯德尔相关系数最大,说明相比于其他中心性方法,NL中心性能够更准确地对节点进行排序。同时,在图2的2个图中也可以看出,k-核分解法的肯德尔相关系数最小,说明k-核分解法对节点重要程度的识别度最低。这是因为k-核分解法给很多节点赋予了相同的ks值,从而不能对这些节点的重要性做进一步的区分。
4 结语
本文提出了一种基于邻居节点和边重要性的多属性节点排序方法——NL中心性算法,该方法从节点周围的子图结构和与其相连的边的重要性这两个方面衡量节点的影响力,在控制时间复杂度的同时还考虑了节点的全局拓扑属性。为了验证所提方法的准确性,将其应用到两个真实的复杂网络中,并且使用SIR传播模型模拟传播过程,然后使用肯德尔相关系数描述中心性算法计算得到的排序结果和传播模型得到的排序结果的拟合程度,最后通过比较结果发现,在两个真实网络中,本文所提方法的准确率都要高于DIL中心性算法,从而说明NL中心性算法可以更准确地找出影响能力大的节点,相比于其他方法可以得到更加精确的排序结果。但是NL中心性算法认为邻居节点和连边对节点重要性的贡献是一样的,没有进一步区分二者的权值。如何给这两个属性赋予合适的权值,是我们下一步的研究方向。
