概念格的一种并行构造算法

李海霞,聂东明,汪慧,王兴龙

（安徽新华学院通识教育部,安徽合肥230088）

20 世纪80 年代,Wille 教授提出了形式概念分析（FCA）,由形式背景,根据偏序关系,可以建立其数据结构——概念格[1].如今,概念格已经被广泛应用于数据挖掘、角色挖掘、医药研究、矿藏开采等多个领域中[2-8].

随着网络技术和数据分布并行存储、处理的发展,同一个数据系统,可能每天都要增加大量的数据,而海量数据需要挖掘其中蕴含的有用信息,多概念的并行构造算法也应运而生[9-11].目前概念格的并行构造一般会利用子概念格原有的信息,不需要遍历概念格的所有节点,算法效率都有明显提高.但不少方法是对原来子概念格的相关节点进行调整,再来确定合并之后概念格节点之间的父子关系.因为概念格中父子关系的确定非常麻烦,后合并生成的节点可能和前面合并生成的不同节点之间均有直接父子关系,所以这项工作量也是很大的.

本文讨论了概念格的一种并行构造算法.构造过程中,子概念格的节点按照内涵的升序排列,并给出了节点级的概念,方便确定并行构造过程中,新生成节点之间的直接父子关系,只需要比较部分级中的部分节点即可自底而上生成新的概念格,同时生成新概念格的Hasse 图.

1 概念格的基本概念

定义1一个形式背景K=（O,D,R）,其中O 是对象集,D 是属性集,xRy 表示对象x 具有属性y.设对象集,属性集定义任意的g∈A,gRm},B"={g∈O| 任意的m∈B,gRm}.若A、B 满足A"=B,B"=A,则称二元组C=（A,B）为一个概念（或节点）,A 称为概念C 的外延（记为Ext（C））,B 称为概念C 的内涵（记为Int（C））[12].

定义2设C1=（A1,B1）和C2=（A2,B2）是两个概念,若（等价于）,称C1为C2的父概念（节点）,C2为C1的子概念（节点）,记为C1≥C2.形式背景K 的所有概念按照这种偏序关系形成的格称为形式背景K 的概念格,记为L（K）.若不存在节点C3,使C1≥C3≥C2,则称C1为C2的直接父概念（节点）,C2为C1的直接子概念（节点）,记为C1＞C2.按照这种偏序关系,所有节点构成了概念格,记为L（O,D,R）,其中最大的节点是（O,O’）,最小的节点是（D,D’）[12].

定义3设两个形式背景K1=（O1,D,R1）和K2=（O2,D,R2）,二者有相同的属性集,K1±K2=（O1∪O2,D,R1∪R2）称为两形式背景的合并[12].

2 概念格的分级合并算法

2.1 相关定义及定理

概念格的合并是将一个子概念格中的节点依次插入另一个子概念格,生成一个新概念格,然后再将一个子概念格插入这个新格中,依次下去,合并生成一个较大的概念格.概念格进行合并时,有两个问题需要处理：新节点的生成和边的更新.为解决上述问题,结合前期的研究工作,给出如下定义和定理.

定理1属性集相同的形式背景对应的概念格L（K1）中的节点C1=（A1,B1）和L（K2）中的节点C2=（A2,B2）若生成一个新节点C,都有C=（A1∪A2,B1∩B2）[13].

定理1 只是解决了新节点的内涵和外延问题,但是还需要判定什么时候才会生成新节点.并行构造中,两子概念格节点内涵的交集如果是第一次出现,一定会生成新节点.而判断内涵的交集是不是第一次出现,如果和先前生成的新节点逐一进行比较,尤其是格结构比较庞大时,比较次数很多,会降低建格速度.为减少比较次数,提高建格效率,需要利用概念格的层次结构.下面给出判断新节点生成和新概念格中节点之间边的关系的相关定理.

定理2两个子概念格的节点按照内涵基的升序排列,将两子格进行合并,则新概念格中父节点一定在子节点之前生成.

因为父节点内涵比子节点的内涵少,即父节点内涵的基小,而两个被合并的子概念格节点是按照内涵基的升序排列的,由两个节点的内涵的交判断是否生成新节点,所以若两新节点之间有父子关系,先生成的节点内涵的基一定小,所以父节点一定在子节点之前生成.

定理3两个子概念格的节点按照内涵基的升序排列,如果概念格L（K1）中的同一节点与概念格L（K2）中的两个不同节点合并时都能生成新节点,则后生成的节点一定是先生成节点的子节点,并且后生成的节点一定是上一个新生成节点的直接子节点.

证明：由定理2,若生成新节点,子节点一定在父节点之后生成.所以,如果概念格L（K1）中的同一节点与概念格L（K2）中的两个节点合并生成新节点之间若有父子关系,则后生成的节点一定是先生成节点的子节点,并且后生成的节点一定是上一个生成节点的直接子节点,所以只要证明生成的两个新节点之间必有父子关系即可.

设节点D1∈L（K1）,节点E1、E2∈L（K2）,D1与E1,D1与E2合并先后生成新节点C1=（A1,B1）和C2=（A2,B2）,所以有B1=int（D1）∩int（E1）,B2=int（D1）∩int（E2）,因为节点是按照内涵升序排列,所以有B1B2,否则不会合并生成新节点,所以节点C1和C2之间有父子关系.假设C2不是节点C1的直接子节点,即二者之间还存在一个新生成的节点C3=（A3,B3）,使得C2＜C3＜C1,其中节点C3也是由格L（K1）中的同一个节点D1和概念格L（K2）中的另一个节点E3合并生成的,则有B3=int（D1）∩int（E3）,且B1B3B2.又因为B1=int（D1）∩int（E1）,B2=int（D1）∩int（E2）,B3=int（D1）∩int（E3）,并且节点C1,C3和C1都是和子格L（K1）中的同一个节点D1合并生成的,所以int（E3）一定比int（E2）少,比int（E1）多,概念格的性质,则在子概念格L（K2）中一定存在节点E2和E3的父节点E,节点E 和子格L（K1）中的同一个节点D1一定也能在新节点C1和C2之间合并生成一个新节点C3,与题设矛盾,所以C2一定是新节点C1的直接子节点.

由定理3,若同一节点与另一子格L（K2）中的两个不同节点合并时都能生成新节点,后生成的节点一定是上一个生成节点的直接子节点,则在Hasse 图中二者即可连边.为方便概念格的合并及其Hasse图的构建,下面给出节点级的定义.

定义4两个子概念格的节点按照内涵基的升序排列,如果子格L（K1）中的节点&i 和另一子格L（K2）中的节点合并能生成一个新节点,则该新节点称为i 级节点,其中i 表示子格L（K1）中的第i 节点.

例如,子概念格L（K1）中的节点&1 和子格L（K2）中的节点合并,若生成新节点,称该节点为1 级节点,为方便格的合并,根据生成的先后次序,分别标记为C1,1,C1,2….

定理4两个子概念格的节点按照内涵基的升序排列,概念格L（K1）中的一个节点与概念格L（K2）中的两个不同节点合并,如果生成的新节点位于同一级,则后生成的节点是先生成节点的子节点,并且后生成的一定是上一个新生成节点的直接子节点.

证明：显然,如果新节点位于同一级,则新节点一定是由一个子格中的同一节点和另一子格中的两个不同节点合并生成的,所以由定理3,即证.

因此,当一个子格中的节点和另一子格中的不同节点合并生成新节点时,它们必然属于同一级,根据标记Ci,j,同一级节点之间只要根据j 的大小次序,即可判断它们之间的父子关系并连边,这将会提高概念格的建格效率.

2.2 算法原理与分析

一般来讲,概念格的时间复杂度是随着节点的个数呈指数级增长,所以在构造过程中应尽量降低节点之间的比较次数来提高建格效率.

由定义4 和以上定理可知,在概念格的合并过程中,子节点会在父节点之后生成.当两个子概念格中的节点按内涵基的升序排列,子格L（K1）中的节点和子格L（K2）中的不同节点都能生成新节点时,后生成的节点一定是上一个生成节点的直接子节点.所以,L（K1）中同一节点和L（K2）进行合并运算时,如果两个子格节点内涵的交集包含于上一个新生成的节点的内涵时,合并运算不会生成新节点；如果内涵的交集包含上一个新生成的节点的内涵时,将会生成一个新节点,并且是该新节点的直接子节点.所以,在同一级中,只需要比较两个要合并的节点内涵的交集与上一个新生成的节点的内涵之间的包含关系,就可以判断是否有新节点生成.另一方面,在不同的级中,节点之间可能也有父子关系,因此也有必要判断两个要合并节点的内涵的交集与其它层节点内涵之间的包含关系,以此来判断是否有新节点生成,及它们之间的之间父子关系.因为合并运算时,子格节点是按内涵基的升序排列的,所以只要和不同级最下面的节点内涵进行比较判断,即可以确定是否有必要进行后续的比较,这也会提高合并运算的效率.

本文定义了概念格节点级的节点,子概念格的节点按照内涵的升序排列,在合并的过程中,两个被合并的节点的内涵的交集（记为集合B）仅与上一个新合并生成的节点作比较,或者自底向上和其他级的部分节点作比较；判断是否生成一个新节点,也不需要和之前生成的所有节点作比较.在同一级中,只要和上一个新生成的节点做比较；在不同的级中,首先和该级最下面的节点作比较以决定是否需要进一步的比较,如果不需要,则转向下一级,如果需要,自底而上进行比较,直到一个节点的内涵包含于集合B（当然此时也一定合并生成一个新节点）,该节点和新生成的节点之间连边,即可转向下一级,直到所有前面定义的级都比较完毕,然后开始下一个合并运算.

在判断一个新节点是否生成时,两新节点之间的直接父子关系也进行了判断,也就是说,节点之间的边进行了更新.因此,不但可以得到所有合并的节点,并且还能得到合并之后的概念格的Hasse 图,此过程也不会产生冗余节点.

2.3 算法描述

算法描述如下：

首先,将子概念格L（K1）和L（K2）中的节点按照内涵的升序排列,生成的新节点标注级.然后,将L（K1）中的每个节点和L（K2）中的每个节点依次合并,在合并过程中,只要判断两节点内涵的交集.如果生成新节点,它的内涵和外延即为两个被合并节点内涵的交集及外延的并集.设两个被合并节点内涵的交集为B,紧邻着刚生成节点为Ci,j=（Aj,Bj）,将会有以下4 种情况：

3 实例

假设有两个形式背景K1=（O1,D,R）和K2=（O2,D,R）,其中对象集O1={1,2,3},O2={4,5},属性集D={a,b,c,d,e},形式背景如表1 和2.

表2 形式背景2Tab.2 Formal context 2

二者的Hasse 图如图1 和图2.

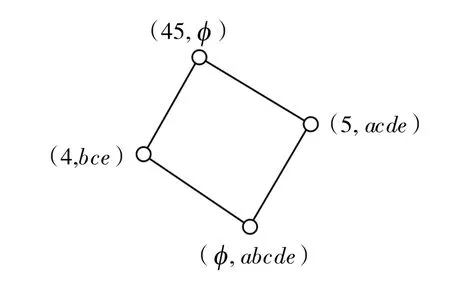
图1 概念格L（K1）的Hasse 图 Fig.1 Hasse diagram of the concept lattice of L（K1）

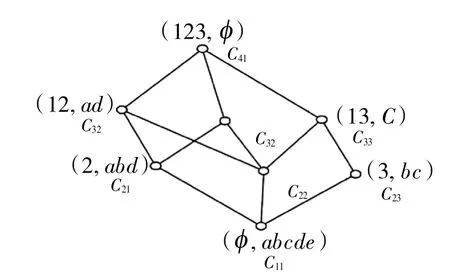
图2 概念格L（K2）的Hasse 图Fig.2 Hasse diagram of the concept lattice of L（K2）

将概念格L（K1）和L（K2）节点按内涵升序排列,L（K1）中节点（45,ce）、（4,bce）、（5,acde）编号分别为&1、&2、&3、&4,L（K2）中节点、（23,b）、（13,c）、（12,ad）、（3,bc）、（1,acd）、（2,abd）a-e）编号分别为#1、#2、#3、#4、#1、#5、#6、#7、#8.根据上述算法,将L（K1）中的点和L（K2）中的节点依次进行合并,合并过程如表3 所示.

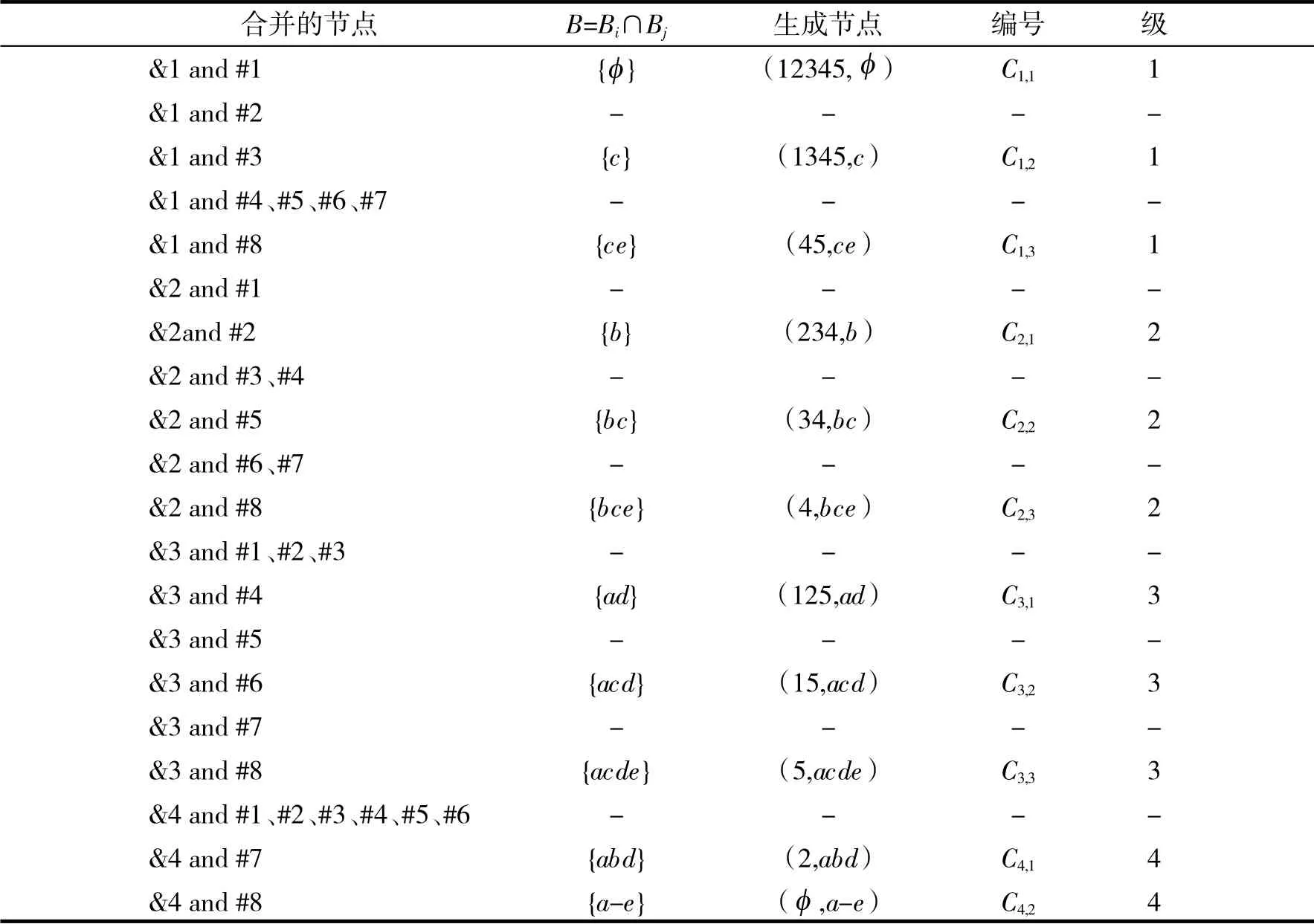
表3 概念格L（K1）和L（K2）的合并过程Tab.3 the merging process of concept lattice L（K1）and L（K1）

由生成节点的级与编号,即可得合并之后新概念格的Hasse 图,见图3.在此过程中,不需要将新生成的节点和前面生成的所有节点进行比较,即可判定是否生成一个新节点及新节点的所有直接父节点,可以极大的提高建格效率.

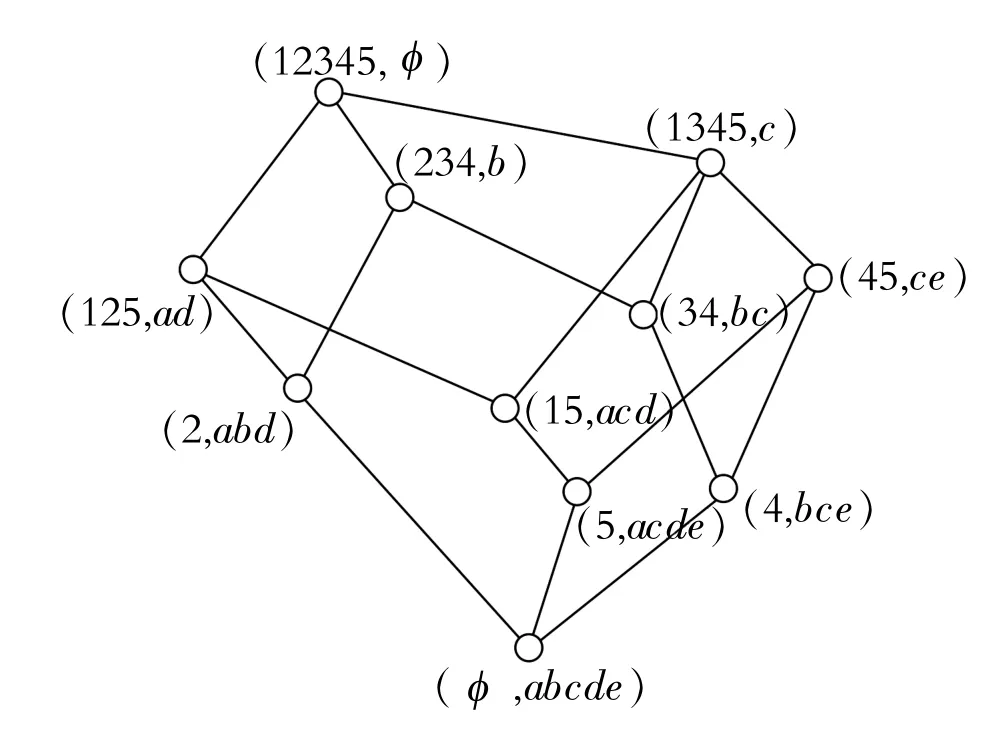
图3 新概念格L（K）的Hasse 图Fig.3 Hasse diagram of the new concept lattice L（K）

4 小结

本文提出了基于节点级的概念格的一种并行构造算法,只需要将新节点和前面刚生成的节点或者部分级中的部分节点自下而上作比较,即可以判定是否生成新节点及节点之间的父子关系,从而得到合并之后概念格的Hasse 图,自上而下构造出新概念格.当然,对概念格的并行构造来讲,如何进一步提高构造效率需继续展开研究.