基于超效率DEA-FKM的城市机动车信号交叉口安全评价研究

于成功,李秀邦，马生元

(1.长安大学汽车学院, 陕西 西安 710061; 2.青海民族大学交通学院, 青海 西宁 810007)

交叉口作为道路交通网络的咽喉，在完成道路衔接和人车交汇中发挥着重要作用。据统计，我国30%的交通事故发生在交叉口[1]。合理地进行交叉口安全评价，对指导交叉口建设、减少交叉口交通事故、提高交叉口运营效率具有重要作用。交叉口安全评价通过对交汇区的各交通要素进行系统分析，定量确定交叉口安全等级，从而对交叉口安全水平进行改善[1]。

交叉口的不安全因素主要由人车在交汇区产生冲突引起，交通冲突是影响交叉口交通运行效率和运营安全的主要因素，多股不同流向的车流在竞争通行权时会产生冲突区域，直接导致了交叉口通行能力的下降和交通秩序的恶化[1]。以交通冲突为方向的研究中，国外侧重于研究不同类型和不同流向的交通冲突[2-3]，国内以研究冲突中机动车和行人运动状态为主[4-5]。获取交通冲突数据的方法主要有基于现场观测冲突和基于仿真冲突两种方法[6]，前者是通过人工观测或者自动视频技术在现场采集交通冲突数据，具有能真实反映实际交通流和费人力的特点；后者是通过仿真平台模拟交叉口测试场景，具有节省人力、评价灵活但结果可能失真的特点。

对交叉口进行安全评价的方法，国内外已有较多研究，主要有模糊综合评价方法、聚类分析、回归分析方法和数据包络分析(DEA)方法[7-8]。模糊评价是通过多因素分析确定指标体系和权重进行分级的方法，但权重赋值主观性强，忽略个体差异，如Ji等[9]提出了一种基于实际信号时序和时延增长率与容量交叉口的综合评价方法。聚类分析是将评价对象指标集合按照接近度进行分类，在数据固定的情况下具有分类精准的特点，如刘涛[10]运用基于冲突数据的灰色聚类法对长安区交叉口进行评价。回归分析方法主要是基于事件观测数据，建立交叉口交通冲突预测模型，并非是对现状的分析，如Zhang等[11]通过摄像机采集交叉口的数据，利用泊松回归，建立了交叉口交通冲突预测模型。

DEA是一种非参数法，通过在生产集内确定生产前沿面计算各生产要素效率，如Djordjevic等[12]利用非径向DEA模型对铁路平面道口(RLCS)进行分析。DEA模型通过最优化方法确定各评价指标权重，避免其他方法带来的主观差异，较好地解决了如何确定评价指标权重的问题[13]。同时DEA是一种输入输出评价，能全面反映生产集的生产效率，避免综合评价或聚类分析的单角度分析问题，在输出中还可以将指标分为期望指标和非期望指标，更适于进行安全评价。DEA灵活、适用性广的特点，既可以进行不同交叉口横向比较，也可以进行同一交叉口时序评价，综合把握安全水平。目前DEA评价中多应用BCC模型，难以对生产前沿面上的决策单元进行比较，而超DEA则可以进一步计算。因此，本文提出一种基于超DEA非期望产出模型结合交通冲突技术来评价交叉口安全的方法，将效率值作为安全评价指数，再运用均值聚类将交叉口分为优、中、差3个安全等级，可有效对城市系统内不同交叉口或者同一交叉口不同时间进行分析，为相关部门提供准确的交叉口安全参数和相关评价指数，以便制定合理措施。

1 评价指标体系的建立与检验

交叉口安全评价指标可以反映交叉口安全的综合状况，因此指标选择要全面，同时指标的选取又受到数据可获性的约束，数据是进行评价的基础。根据交通安全分析中的人-车-路(环境)综合分析，依据科学性、可靠性、全面性、操作性和可比性原则，选取具有表征性强、指标可量化、概念简明、相对独立等特点的指标。评价指标体系构建见图1。

图1 评价指标体系Fig.1 Evaluation index system

(1)交叉口交通量x1。指在一定时间内通过指定交叉口的总数，可根据车辆换算系数求出当量交通量，是体现交叉口服务水平的直接指标。

(2)平均通过速度比x2。车辆在获得通过相位内通过交叉口时的平均速度与上游路段平均速度之比，是一项反应交叉口行车秩序、行人干扰、管理水平的综合指标。

(3)平均延误时间x3。车辆在交叉口由于某些原因处于静止状态所产生的延误，为停车时间、车辆启动反应时间之和，有效反应交叉口畅通度和不同相位的影响。

(4)交叉口饱和度x4。道路饱和度是交通量v与通行能力c的比值，交叉口饱和度取各进口道饱和度以进口道流量为权的加权平均值，是反应交叉口宏观运行状态的指标。

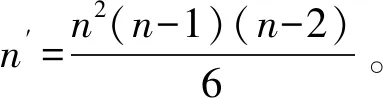
(6)机动车交通冲突y。指不同的机动车参与者之间在时间和空间上产生了严重的相互干扰,迫使至少一个参与者采取了避让行为,因此交通冲突是交通事故发生的底层现象，是评价交叉口安全的重要指标。包括追尾冲突和交叉类冲突(包括交叉冲突、分流点、交汇点和路口的4种类型冲突)。 部分冲突示意图见图2[10]，第3类冲突可以使用信号灯控制以避免发生：

运用SPSS软件对指标进行复相关性分析。各输入变量与输出变量的相关系数值、显著性p值、检验水平及回归模型的调整R2如表1所示，由表1可见，除x5的相关性为0.619，为弱相关，其余相关性值均接近或大于0.80，相关性较强。在0.05检验水平下所有输入指标的p值均不大于0.05，且调整R2为0.992，说明输入输出指标显著相关。因此，可建立评价指标体系为：X={x1,x2,x3,x4,x5}，Y={y}。

2 评价模型构建

2.1 超效率DEA交叉口安全评价指数模型

(4)

式中，hj0为第j0个交叉口的评价指数，μi为第i个输入变量的权重。

(5)

当θ0=1，且s0+=s0-=0时，则评价对象j0为DEA有效，第j0个交叉口为技术有效和规模有效；当θ0=1，但存在某个输入或输出大于0，则称评价对象j0为弱DEA有效，即技术效率和规模非同时最佳；当θ0<1,评价对象j0为非DEA有效，即技术效率和规模均非最佳。

当问题最优解是非DEA有效时，可以对评价对象的输入和输出进行调整。

(6)

为量化C2R模型中DEA有效评价对象的差异性，在对偶问题D的基础上进行超效率DEA计算，在C2R模型中的有效评价对象统一为1，而在超效率DEA中可以进一步根据决策单元输入输出的优劣程度计算出具体差异数值。超DEA模型与C2R模型相似，不同之处在于进行第j0个交叉口评价时，使第j0个交叉口的输入和输出被其他所有的交叉口输入输出的线性组合替代，而将第j0个交叉口排除在外：

(7)

2.2 交叉口安全等级划分模型

采用K均值聚类，将求解的各交叉口安全评价指数H={h1,h2,…,hn}作为K值，聚类成安全性分别为优、中、差3类的交叉口，为避免陷入局部最优解，对K均值聚类算法进行初始簇中心改进,使初始簇中心保持一定距离，分布更加均匀。本文初始簇中心集合为：

M={mk}={maxH,medH,minH}。

(8)

3 模型应用实例

选取西宁市城中区10个交叉口进行实例分析。对于交叉口交通量、相位配时、车道数和机动车交通冲突采用人工调查法, 调查时间选择2017年6月12日—16日早高峰 (7∶30—9∶00) 和晚高峰 (17∶30—19∶00) 时段。具体调查在交叉口进口道进行, 人工统计各类车辆左、直、右3个驶向交通量和冲突次数,采用Aidaroe软件根据交叉口不同方向交通量和相位配时数据仿真出平均延误时间、饱和度和通过速度比。高峰小时下统计及仿真各指标平均数据见表2。

表2 评价指标数据

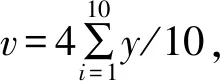
表3 DEA安全评价指数

由表3可见，交叉口2、4、5、10的C2R评价指数为1，即DEA有效，其有效前沿面投影为自身，交叉口运营安全状况较好。而其余6个交叉口均为DEA无效，意味着运营安全性相对较差，应对交叉口进行改进管制。可以根据非DEA有效交叉口在生产前沿面上的投影是有效的原则进行改进，通过对输入输出投影进行分析找出影响各交叉口运营安全的主要因素。

将求解的C2R评价指数和超效率DEA评价指数分别代入式(8)进行聚类步骤，聚类结果见表4。

表4 安全评价分级结果

由表4可见，由于C2R评价指数中有效评价对象均为1，因此用该指数进行聚类时容易陷入偏聚类现象，使得交叉口安全等级评价更多为优。而采用超效率DEA指数聚类，则可避免这一现象。

4 结束语

本文提出一种针对不同评价条件的灵活指标体系，构建了只包含非期望输出的C2R模型。在C2R模型基础上，针对评价对象为有效的评价单元，建立了超效率DEA分析模型，准确量化各交叉口参数之间的差异。以超效率DEA评价指数和FKM方法为基础，改进初始簇聚类中心，有效避免局部最优解现象。以西宁市交叉口为例，验证了方法可行性。

本文所提出的评价方法对研究和分析城市交叉口安全具有参考价值，丰富了交叉口安全评价方法。未来研究中将进一步增加更为复杂的影响因素,比如天气因素、不同日期下的同一交叉口安全特性等，为相关部门制定更为合理的交通安全措施提供依据。