基于混沌理论和MEA-BPNN模型的快速路短时交通流预测
2019-04-19王硕谷远利李萌陆文琦张源
王硕,谷远利,李萌,陆文琦,张源
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
随着信息和大数据技术的发展,基于智能交通系统(intelligent transport system, ITS)的道路交通管理和控制被广泛运用于解决交通拥堵、缓解道路压力等方面。其中,道路管控的可行性和高效性依赖于以交通流预测为基础的交通状况预测,而且精准的交通流预测对于实现主动交通管理等先进管控手段具有重要意义[1]。道路网短时交通流预测是在实测交通流数据的基础上预测下一时段的交通流量,为提高短时交通流的预测效果,国内外交通行业研究者从构建模型的角度进行了大量的研究。从20世纪60年代开始,多种有效的交通流预测模型和算法涌现,比较常见的模型包括基于线性理论的模型如历史平均模型(history average model, HAM)、卡尔曼滤波模型(Kalman filtering model, KFM)、滑动平均模型(moving average model, MAM)等,基于非线性理论的模型如小波分析模型(wavelet model, WM)和混沌理论模型(chaos theory model, CTM)等,以及基于智能理论的模型如神经网络(neural network, NM)和支持向量机(support vector machine, SVM)等[2-5]。其中,混沌理论预测模型具有直接基于交通流时间序列数据内在的规律性进行分析预测,不必建立主观模型从而避免人工干预的优点,神经网络预测模型则具有不用求解具体的拟合函数以及可逼近任意非线性问题等显著的优势。但在进行神经网络建模时,输入向量的选择多由研究者主观分析得到,所以模型预测精确度受到人为干预。由于混沌理论模型和神经网络模型各有所长,而组合预测模型能融合不同模型的优点,提高预测精确度[6],所以本文主要研究基于混沌理论和改进神经网络的组合预测方法。
混沌理论最早由气象学研究学者Lorenz提出并应用于大气对流模型中,随后不断发展并应用于天文、医学、能源、金融等行业的时间序列数据研究。Takens[7]提出了相空间重构方法来研究混沌时间序列,通过重构单一时间序列还原系统的混沌性,从而发现时间序列的隐含规律,开启了混沌理论的定量研究。宗春光等[8]将混沌理论引入到交通流预测方法中,利用相空间重构的分析方法处理数据,并进行了线性回归预测,证明了相空间重构在交通流预测中的有效性,但交通流数据具有明显的非线性,线性方法无法准确描述其演变规律。
BP神经网络作为一种误差反向传播的神经网络,具有强大的非线性逼近能力,并具有优越的稳定性和容错性,是目前应用最广泛的人工神经网络模型之一,但由于BP神经网络采用梯度下降法训练初始权值和阈值,具有收敛速度慢且易陷入局部最优解的缺陷[9]。
本文创新性地将混沌理论和改进BP神经网络进行融合,构建组合预测模型。针对BP神经网络自身的缺陷,利用思维进化算法(mind evolution algorithm,MEA)来优化BP神经网络,MEA在传统遗传算法中“群体”和“进化”思想的基础上,引入了“趋同”和“异化”操作,具有更强大的全局搜索能力且克服了传统遗传算法[10-11]结果不可知、早熟收敛的缺陷,能够提升BP神经网络的预测效果。为检验提出模型的预测精度,本文利用北京市二环路两周工作日交通流数据进行了短时交通流预测,和单一模型预测结果进行误差对比,证明了所提组合模型预测精度的优越性。
1 快速路交通流数据特性
城市快速路交通系统是一个由人、车、路、环境共同作用、交叉影响的开放系统。驾驶人出行的规律性,使得交通流表现出一定规律性和稳定性,具体表现为交通流的时空特性。而随着观测尺度的缩短,交通流变化易受到驾驶人生理心理状况、路况和环境等因素的影响,体现出较强的随机性和波动性特征。交通流数据既具有规律性又具有随机性,使其表现出混沌性的特点。
为了解交通流数据特性,选取北京市二环快速路上连续10个断面交通流数据在两周内的持续变化进行分析。数据由微波检测器获得,研究断面位于阜成门桥北到钟楼北桥之间。
1.1 时空特性
1.1.1 相似性
随机选取某一断面两周工作日数据,对数据进行平滑后,得到交通流随时间变化的曲线,如图1所示。整体来看,各工作日之间交通流量表现出强相似性,均表现出稳定阶段、增长阶段、早高峰阶段和晚高峰阶段,两周之间也呈现出周相似性,故案例分析中可选择连续两周工作日交通流数据作为研究对象。
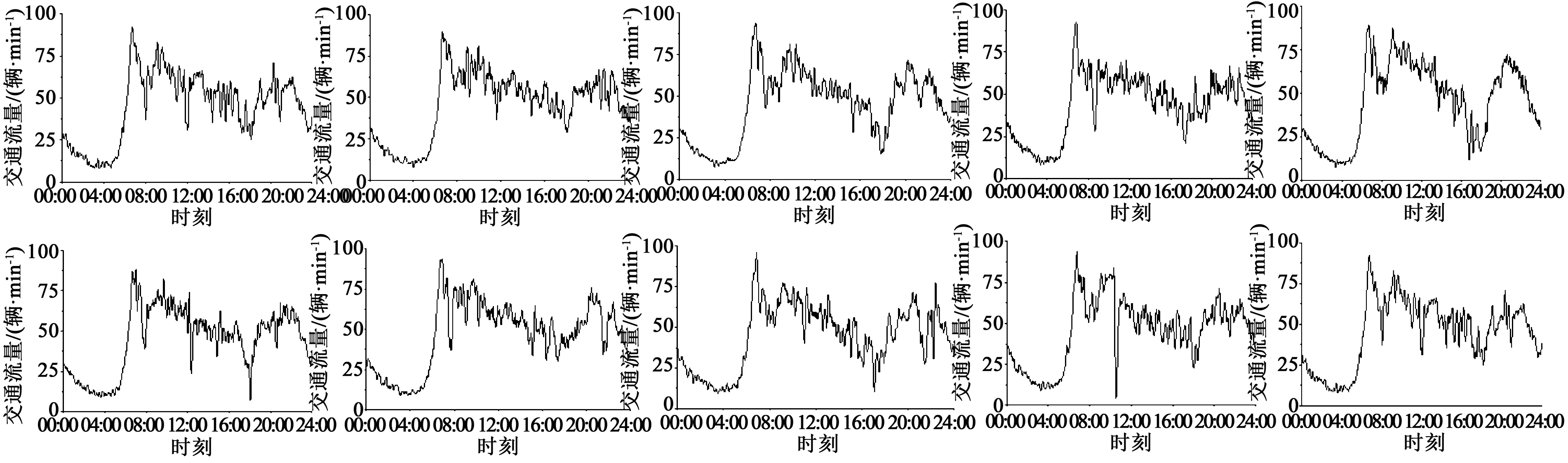
图1 两周工作日交通流量图Fig.1 Traffic flow chart of consecutive two-week workdays
1.1.2 周期性
随机选取某一断面两周工作日数据,进行快速傅里叶变换(fast Fourier transform ,FFT),得到时域图和频谱图如图2所示,其中时域图横轴为时间,纵轴为交通流量,频谱图横轴为数据采样频率,纵轴为振幅。由时域图可以看出交通流在时间上具有明显的周期性,频谱图则将时域的信号转变为频域的信号,在频率0.001 3到0.001 4处出现冲击波,取倒数可得数列的周期P≈720,由于实验数据采集间隔2 min,720为一天所采集的交通流数据量,故由频谱分析得到交通流具有周期性且其周期为1 d。

图2 交通流量时域图和频谱图Fig.2 Time domain and spectrum charts of traffic flow
1.1.3 空间相关性
研究交通流空间相关性即分析断面交通流之间的相关关系,找出相关度较高的几个相邻断面作为接下来的研究对象,一方面可以简化模型,避免输入向量过于庞大造成模型复杂、速度慢等问题,另一方面能防止相关性较弱的断面相互干扰,提高预测精度。
采用多元统计分析中的聚类分析方法来分析各个断面交通流之间的相关关系,本文采用层次凝聚聚类(hierarchical agglomerative clustering ,HAC)方法进行聚类[12],该聚类算法的方法和评价标准是将每组数据作为一类,计算类别之间的欧式距离,合并两个相似的类为一大类,重复该步骤直到所有组合并为一大类,利用HAC方法可以形成一个树状图来表示聚类结果。
选取1.1.1交通流时间序列,按照层次聚类步骤进行聚类分析,对10个断面交通流数据进行层次聚类得到聚类树状图见图3。
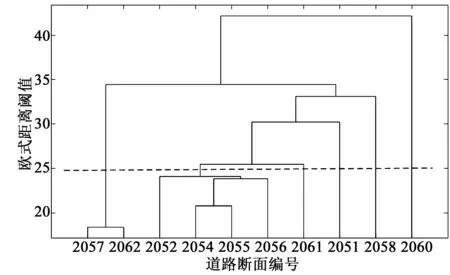
图3 聚类树状图Fig.3 Dendrogram of cluster
层次聚类方法得到的树状谱系图表示相似程度,本文中交通流时间序列的相似度由欧式距离来计算,距离越小表示相似度越高。由图3可得,在阈值25时断面被分为6类,其中有4个编号为2052、2054、2055和2056的相邻断面被分为一类,可以视为该4个相邻断面相似度较高,既具有空间上的联系,又具有反映该4个断面所属路段交通流变化特征的意义。故接下来的案例分析可选择北京市二环路上这4个断面交通流数据进行结合时空特征的交通流多断面预测工作。
1.2 混沌性
本文采用Lyapunov指数法来判定交通流数据的混沌性,Lyapunov指数大于0即判定系统为混沌。首先对时间序列数据进行相空间重构,延迟时间τ和嵌入维数d是进行相空间重构的重要参数。
1.2.1 时间延迟τ和嵌入维数d
τ表示将一维交通流数据展开到高维坐标系后,每个坐标轴的相位差,即重构后每个坐标点中相邻两维交通流数据分量之间的时间差为τ;嵌入维数d 是相空间重构后得到的维数,将时间序列数据扩展到d维坐标系中,即相空间重构后每个坐标点有d 维坐标分量。
在相空间重构中τ和d 的取值直接影响重构效果。如果τ的取值太小,重构后所有坐标轴几乎是一致的,相空间轨迹无法展开;如果τ的取值太大,则相空间轨迹容易间断且过于复杂。如果d的取值太小,无法展现出相空间轨迹的规律性;如果d 的取值太大,则会增大Lyapunov指数等的计算复杂度。目前τ和d 的选择主要由数学方法计算得出,本文采用C-C关联积分法同时确定出τ和d。
C-C算法由Kim等[13-14]于1999年首次提出,是一种能同时估算出延迟时间τ和嵌入窗宽τm的方法。设有长度为N的交通流时间序列xi={x1,x2,…,xN},C-C关联积分法求解延迟时间τ和嵌入窗宽τm的步骤如下:
首先定义嵌入交通流时间序列的关联积分:

其次定义关联维数:
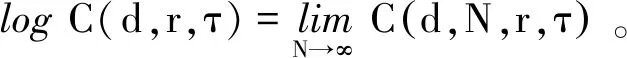
将交通流时间序列分成t个子序列,分别为:
{x1,x1+t,…,x1+(d-1)t},{x2,x2+t,…,x2+(d-1)t},…, {xi,xi+t,…,xi+(d-1)t},…,{xt,x2t,…,xdt}。
定义每个交通流子序列的统计量:
当N有限时,S(d,r,t)取零点值或对全部取值差别最小的值,选择对应值分别最大和最小的半径r,定义差值:
ΔS(d,t)=max{S(d,rj,t,N)}-min{S(d,ri,t,N)}(i≠j)。
ΔS(d,t)为半径r的最大偏差,t为其最小值,时间延迟τ对应着第一个t,根据统计结论有以下公式:

1.2.2 小数量法判定混沌性
Lyapunov指数为定量描述混沌时间序列数据里两个初始值相互分离速率的指标,一个混沌时间序列中存在着多个Lyapunov指数,最大值为最大Lyapunvo指数,是识别混沌特性的关键指标,只要最大Lyapunov指数大于0,系统就可以被判定为混沌[15]。
本文选取具有样本需求量少、计算速度快等优点的小数量法[16]计算最大Lyapunov指数来进行混沌识别,小数量法算法首先根据延迟时间τ和嵌入维数m对时间序列进行相空间重构,然后寻找每个相点的最近邻点,即:

通过每个点最近临近点的平均发散率估计得最大Lyapunov指数,即

当λ<0时,系统是稳定的;当λ=0时,系统具有周期变化性;当λ>0时,系统具有混沌性。
2 基于思维进化算法优化的BP神经网络
BP神经网络由Rumelhart等[17]于1986年首次提出,是一种误差逆向传播的多层前馈神经网络,作为目前应用最广泛的神经网络模型之一,BPNN具有可塑性好、操作简单和可任意逼近非线性映射的优点。其由输入层、隐含层和输出层组成,层与层神经元之间通过权值和阈值相互连接,层内神经元相互独立,其预测功能通过对模型进行训练实现。
MEA由孙承意等[18]于2000年首次提出,该算法是一种模拟人类思维进化过程的算法,其关键步骤在于“趋同”和“异化”,趋同即在进化过程中不断向优胜者学习进而被优胜群体同化,异化则是优胜群体中的个体会自我改善,进而融入到更优胜群体中。在反复“趋同”和“异化”过程中,最终优胜劣汰,全局产生唯一优胜群体,即得到全局最优解。
结合BPNN可塑性好且操作简单以及MEA全局搜索能力强的优点,本文采用MEA-BPNN算法来进行快速路交通流量的短时预测。MEA-BPNN算法步骤如下:
Step1:建立BP神经网络模型,确定初始权值和阈值;
Step2:进行MEA初始设置,随机产生P个个体,代表不同初始权值阈值的BP神经网络模型,并将个体划分到优胜子群体和临时子群体里;
Step3:执行趋同操作,计算单个群体中的个体得分,定义最高分为优胜者并在局部公告板和全局公告板上显示,更新产生新的子群体,重复趋同操作直到优胜者的得分不再增高,定义优胜者的得分为该子群体得分;
Step4:执行异化操作,子群体在全局范围内进行竞争,淘汰并产生新的临时子群体,重复趋同异化操作直到满足迭代终止条件;
Step5:根据MEA编码规则,解析出最优个体,得到最优权值和阈值;
Step6:将优化得到的权值和阈值作为BPNN参数,用重构交通流时间序列数据对BPNN进行预测。

图4 MEA-BPNN算法流程图Fig.4 Flow chart of MEA-BPNN algorithm
3 案例分析
3.1 相空间重构
选择在空间相关性上聚为一类的北京市二环路4个连续断面作为研究对象,对其两周工作日交通流数据,按照C-C算法步骤进行时间延迟τ和嵌入窗宽τm的计算,结果如图5所示。
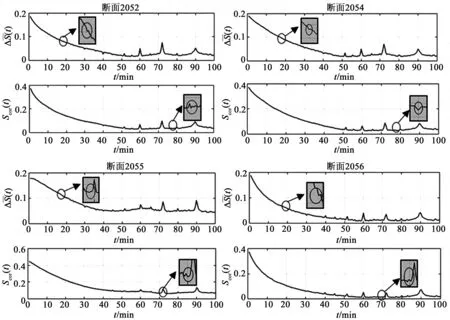
图5 C-C算法结果图Fig. 5 C-C algorithm result maps

τm=(d-1)τ。
则可用C-C方法同时确定延迟时间τ和嵌入维数d, 再根据小数量法计算最大Lyapunvo指数,得到如表1所示的各断面相空间重构参数。

表1 重构参数表
4个断面的最大Lyapunvo指数均大于0,即交通流时间序列数据具有混沌特性。求得延迟时间τ和嵌入维数d后,按照Cao[19]所提出的相空间重构方法,可以得到一个与原交通流时间序列等价的相空间,建立d维坐标系,相空间轨迹由d维坐标系中的点组成,每个点叫做相空间的一个相点,设为Vn,则:
式中,m为参与重构的时间序列维数,n代表相空间中第n个相点,τ也叫坐标延迟,代表重构后高维坐标系坐标轴之间的相位差,d为重构后所得相空间的维数。本文里m=4,代表4组来自于不同断面的交通流量,τ和d分别代表重构交通流时间序列数据中两相邻维之间的时间步数和重构交通流时间序列数据的维数。

3.2 预测过程和结果
本文构建的MEA-BPNN模型具有20个输入向量,4个输出向量,可以实现4个断面的同时预测,模型参数设置见表2。

表2 MEA-BPNN初始参数设置
利用MEA算法对BP神经网络初始权值和阈值进行优化的过程中,对应的初代优胜子种群和初代临时子种群的趋同过程如图6所示。由图6可知,经过几次趋同操作后各子种群得分不再增加,种群已经成熟,其后进行异化操作,增加新的个体,循环直到得到最优个体,即得出了优化算法最优解,对应BPNN最优权值和阈值。

图6 初始子种群趋同过程Fig. 6 Convergence process of the initial superior and temporary subpopulation
利用MEA优化得出的权值和阈值,改进BPNN模型后再利用前文中得出的数据训练集进行训练,BPNN同时输出4个断面的一日交通量预测值,预测效果见图7,可直观看出预测值和实际交通量趋势一致,预测效果较好。
3.3 结果分析
为了对比分析相空间重构和MEA-BPNN模型的有效性,本文对4个断面的交通流量分别进行了无重构的MEA-BPNN模型预测以及重构、无重构的BPNN模型预测,用均方根误差(rootmeansquareerror,RMSE)、平均绝对误差(meanaverageerror,MAE)和平均绝对百分误差(meanaveragepercentageerror,MAPE)3种误差评价指标进行了模型精确度的评价,结果如表3所示。
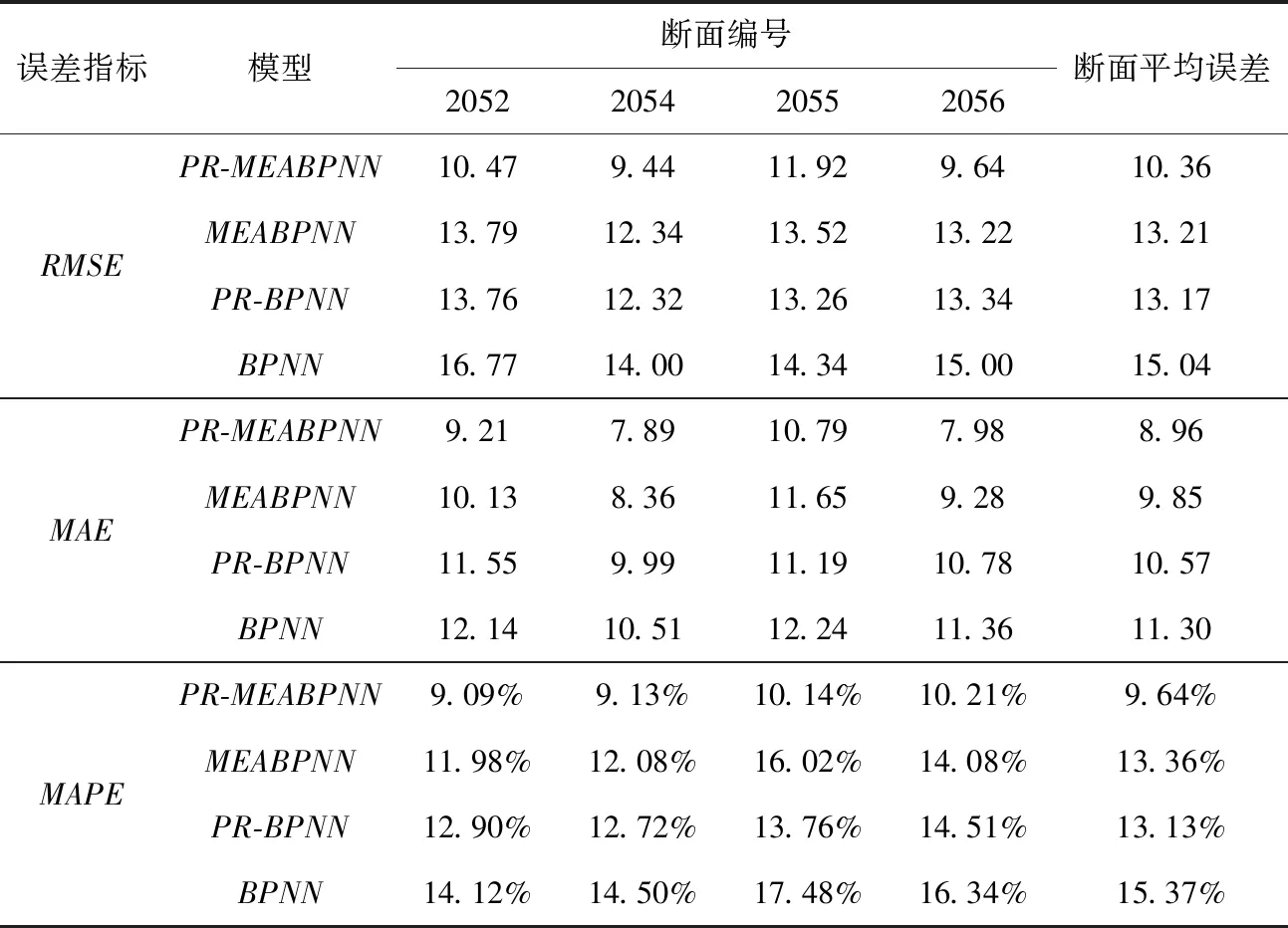
表3 误差对比
由表3可见,基于PR-BPNN模型的断面平均误差与基于传统BPNN模型的断面平均误差相比,均方根误差、平均绝对误差和平均绝对百分误差分别下降12.43%,6.46%和14.57%,证明了相空间重构处理交通流数据的有效性;基于MEA-BPNN模型的断面平均误差与基于传统BPNN模型的断面平均误差相比,均方根误差、平均绝对误差和平均绝对百分误差分别下降12.16%,12.83%和13.73%,证明了MEA在改进BPNN模型方面的有效性;基于PR-MEABPNN模型的断面平均误差与基于传统BPNN模型的断面平均误差相比,均方根误差、平均绝对误差和平均绝对百分误差分别下降31.11%,20.71%和37.28%,证明了组合预测模型同时具备相空间重构和思维进化算法改进BPNN模型的优越性,提高了交通流预测精度。
4 结语
本文结合实测数据进行了交通流的时空特征和混沌分析,证明了交通流数据时间上具有相似性与周期性,空间上具有断面相关性,且判定了其具有混沌特性。根据交通流的时空特性选定了预测的时段和路段,并根据混沌特性进行了相空间重构,优化了模型输入。提出了MEA改进后的BPNN模型,并进行了相空间重构和改进BPNN模型融合的道路网多断面的短时交通流预测,与未改进模型进行了误差对比,证明了改进算法具有更高的预测精度,预测结果可为出行决策和交通管控提供更准确的参考。
本文在进行预测时,只考虑了交通流量时间序列本身的变化规律,进一步的工作中可考虑交通流三要素之间的相互影响,将其他交通要素如速度和占有率加入相空间重构,用多变量相空间重构的方法更全面地反映交通流变化规律。
