乘法半群为矩形群的nil扩张的半环

蒲楠，李刚

(山东师范大学数学与统计学院，山东 济南 250014)

1 引言及预备知识

设(S,·)为半群，对于任意的a∈S, 若存在x∈S, 使得a=axa, 则称a为S的正则元。 若半群S的每一个元素都是正则元，则称S是正则半群[1]。若对于正则半群S及任意的a∈S，存在x∈S, 使得a=axa,x=xax且ax=xa，则称S为完全正则半群。Petrichm等[2]深入地研究了完全正则半群，从幂等元的角度对完全正则半群进行了分类。 例如设S为完全正则半群，E(S)表示S的幂等元集，若E(S)为矩形带，即对于任意的e,f∈S,有e=efe，则称S为矩形群。

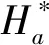
半环(S,+,·)是一个带有二元运算“+”和“·”的代数，满足以下条件：

(1)(S,+)是一个半群；

(2)(S,·)是一个半群；

(3)(a,b∈S)满足分配律，a(b+c)=ab+ac,(a+b)c=ac+bc。

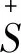
定义1[1]H*,L*,R*表示S上的Green*关系。 其中H*,L*,R*分别为:

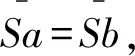
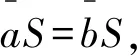
H*=L*∨R*。

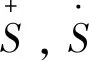
1 乘法半群为矩形群的nil扩张的半环

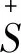
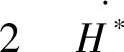
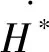
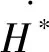
考虑半环S的子集Q1={a|a∈S,a+a0=a0}，对于任意的a∈S,a0+a0=a0，所以Q1为S的非空集合。

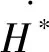
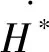
a0b0=(a+a0)(b+b0)

=a(b+b0)+a0(b+b0)

=ab+ab0+a0b0

=ab+(a+a0)b0

=ab+a0b0，

即(ab)0=ab+(ab)0，从而ab∈Q1，则Q1为S的子半群。

类似的，考虑半环S的子集Q2={a|a∈S,a′∈Q1}，对于任意的a∈S,(a0)′=a0∈Q1，所以Q2为S的非空集合。

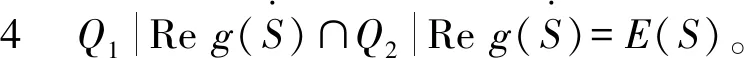
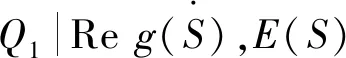
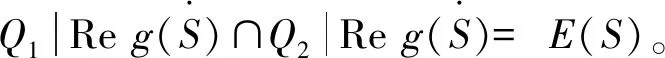
定义半环S上的关系：

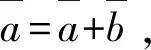
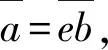
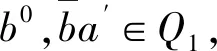
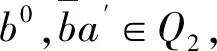
定理1 设半环S满足∀

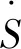
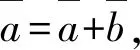
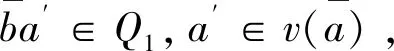
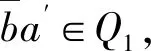
因此a≤.b，从而≤.⊆≤0。

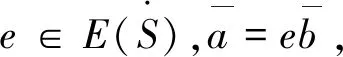
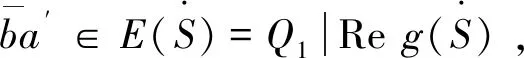
同理可证≤0=≤.。

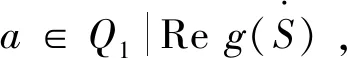
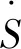
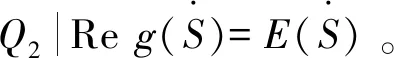
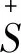
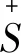
考虑半环S的子集Q3={a|a∈S,aa0=a0}，对于任意的a∈S,a0a0=a0，所以Q3为S的非空集合。

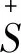
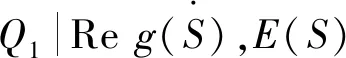
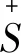
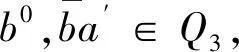
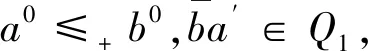
≤+,≤0,≤0定义如上。

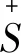
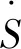
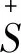
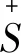
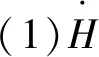
(2)≤+=≤*；

(3)对于任意的a,b∈S，(a0+b0)0=(a+b)0。