三角形垂心的一个有趣性质——兼擂题(121)的解答

重庆市长寿龙溪中学 (邮编：401249)

《中学数学教学》2019年第1期上的擂题(121)是赵忠华老师提供的一个有趣的几何问题：

擂题(121) 设H是△ABC的垂心，J为BC的中点，点M，N在边BC上，BM=CN，且B，M，N，C四点按此顺序排列．过H且垂直于HM的直线交AB于点E，过H且垂直于HN的直线交AC于点F，则JH⊥EF.

下面我们用坐标法证明这个命题．

证明如图1，设AO是△ABC的BC边上的高．

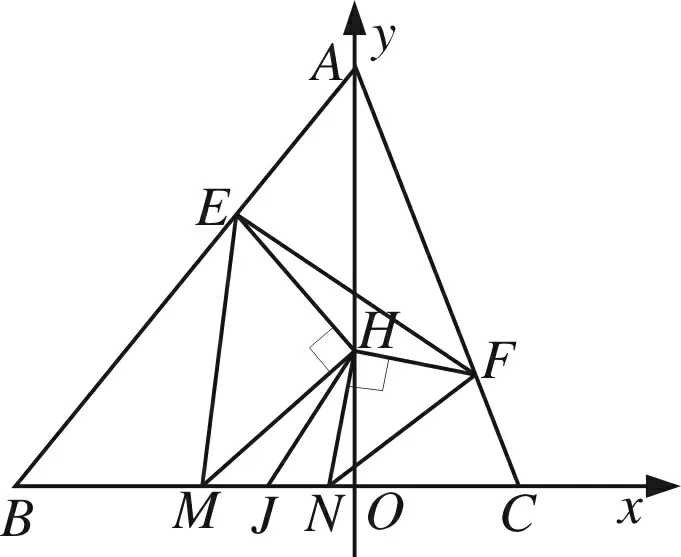
图1

以BC所在直线为x轴，以AO所在直线为y轴建立如图所示的平面直角坐标系．易知(R为△ABC外接圆半径)：

A(0，2RsinBsinC)，B(-2RcosBsinC，0)，C(2RsinBcosC，0)，H(0，2RcosBcosC)．

则BC的中点J为(Rsin(B-C)，0)．

又设M(-2RcosBsinC+m，0)，N(2RsinBcosC-m，0)(其中m≠a=2RsinA)．

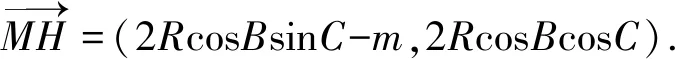
而EH⊥MH，可求得HE的方程为：

x(2RcosBsinC-m)+2yRcosBcosC=4R2cos2Bcos2C．

又，AB的方程为：

xsinB-ycosB=-2RsinBcosBsinC．

解得两直线的交点E的坐标为：

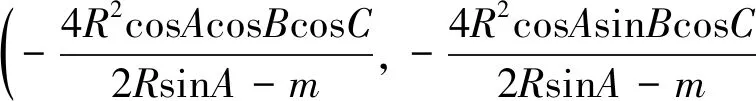
同理可得F的坐标为：

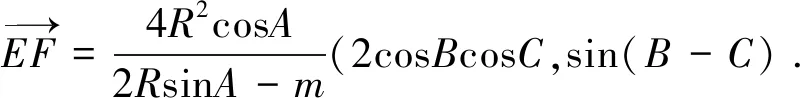
注参数m不能取a(否则题设中的E，F将不存在)，除此外，m可取其它任意实数值．这表明：擂题中只需M，N在直线BC上且关于J对称(但不能与B，C重合)即可，不必限定为图1中的顺序．

下面给出该擂题的若干有趣推论．

推论1 如图1，在擂题(121)条件下，△MHE与△NHF反向相似．

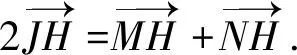
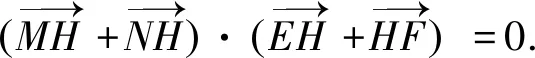
显然，上式左边两向量的夹角与右边两向量的夹角相等，因此有：

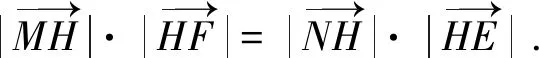
由此易知：△MHE∽△NHF．

而它们的对应顶点绕向相反，所以是反向相似．证毕．

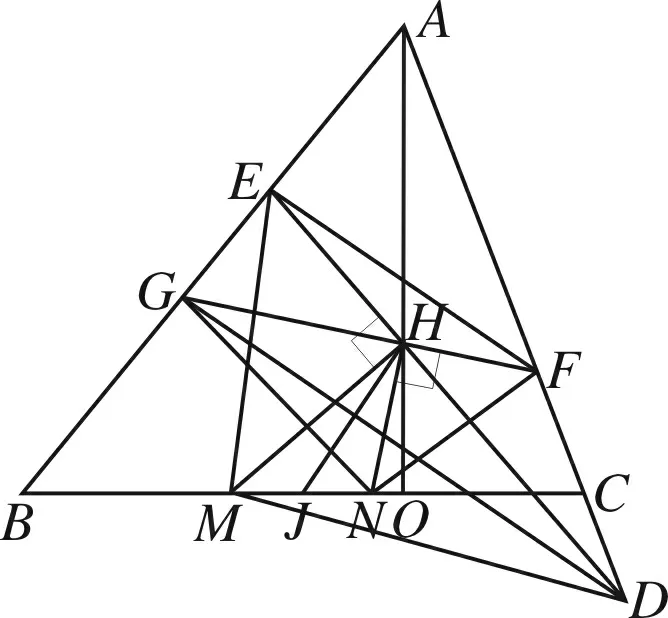
图2

推论2 如图2，H是△ABC的垂心，J为BC的中点．M，N在直线BC上且关于J对称．过H且垂直于HM的直线交直线AC于点D，交直线AB于点E；过H且垂直于HN的直线交AC于点F，交直线AB于点G，则(i)EF//DG；(ii) △MDE与△NGF反向相似．

证明(i)擂题中已证：JH⊥EF．同理可证：JH⊥DG．所以EF//DG．

(ii)推论1中已证△MHE与△NHF反向相似．同理可证：△MHD与△NHG反向相似．并且这两对相似三角形的相似比都是|MH|:|NH|．由此易得结论．证毕．

另外，注意到擂题的证明中得到的E，F的横坐标互为相反数，即有：

推论3 如图1，在擂题(121)条件下，则BC边上的高AO平分EF．

特别地，当M、N与J重合时，EF过垂心H，由推论3得：

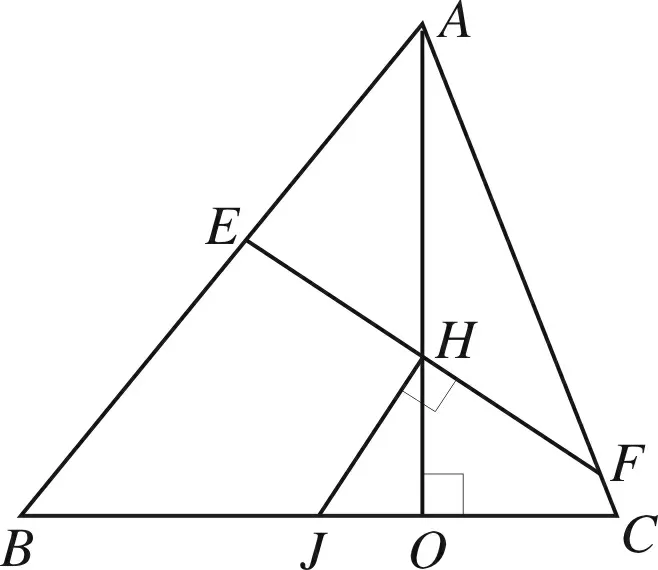
图3

推论4 如图3，设H是△ABC的垂心，J为BC的中点，过H且垂直于HJ的直线交直线AB于点E，交直线AC于点F，则H是EF的中点．

评注(评注人：郭要红，2019年3月31日) 本擂题收到正确攻擂稿件4份，按时间顺序，作者依次是吴波(重庆市长寿龙溪中学，401249，2019年2月22日)，张云华(四川省成都华西中学，610051,2019年2月23日)，个屋院(2019年2月24日)，孙纯祥(忠县临港初级中学，404342,2019年2月27日)。我们选择刊登吴波老师的来稿作为本擂题的解答，吴老师也是擂题奖金的获得者. 文章署名表明作者拥有文章的著作权与文责自负，恳请作者来稿注明真实姓名。