关于Milosevic不等式的加强

山东威海职业学院艺术设计系 (邮编：264210 )

设△ABC的三边长为a、b、c，外接圆和内切圆半径分别为R、r，半周长为s，面积为△，∑表示循环求和.

文[1]介绍了由D.M.Milosevic提出的如下一个不等式

①

这是一个形式简洁，优美的不等式.

由三角形中常见的不等式

我们自然考虑①的如下加强

②

实际上，我们可以证明较②更强的结果

定理1 在△ABC中，有

③

其中等号当且仅当三角形△ABC为正三角形时取得.

证明由积化和差公式，可得

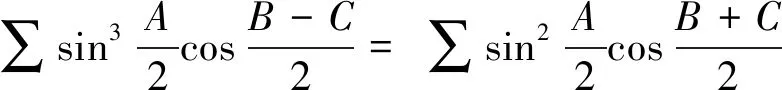
④

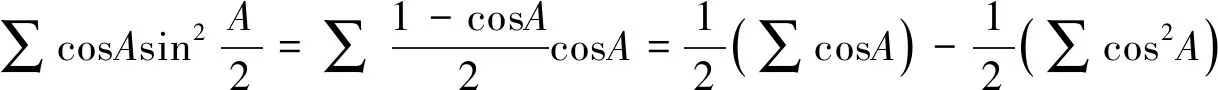
⑤

由三角形中熟知的恒等式

⑥

⑦

⑧

将⑥、⑦和⑧代入④和⑤, 整理可得

⑨

由⑨及Gerretsen不等式

s2≤4R2+4Rr+3r2,

即得③，从而定理1成立.

推论在△ABC中,

由欧拉不等式R≥2r,可知推论比②强.

注本文受威海职业学院科研项目基金资助，编号2016ky001.