Garfunkel—Bankoff 不等式的一个类似

陕西咸阳师范学院基础教育研究课程中心 (邮编： 712000 )

文[1]-[4]多次研究了如下Garfunkel—Bankoff 不等式:

问题1 在△ABC中，

①

等号当且仅当△ABC为正三角形时成立.

通过探究，发现了不等式①的一个如下类似：

问题2 在△ABC中，R,r表示三角形外接圆和内切圆半径，则有

②

等号当且仅当△ABC为正三角形时成立.

证明记△ABC的三边长为a、b、c,则存在正数x、y、z，使得

a=y+z,b=z+x,c=x+y.

这时，可以求得(文[5])

(*)

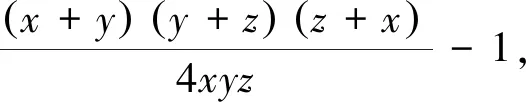
注意到文[6]里的恒等式：

(x+y)(y+z)(z+x)=(x+y+z)(xy+yz+zx)-xyz.

立知(*)等价于

4(yz)2+4(zx)2+4(xy)2≤(x+y+z)2(xy+yz+zx)-5xyz(x+y+z),等价于

4(yz)2+4(zx)2+4(xy)2≤(x2+y2+z2)(xy+yz+zx)+2(xy+yz+zx)2-5xyz(x+y+z),等价于

2(yz)2+2(zx)2+2(xy)2≤(x2+y2+z2)(xy+yz+zx)-xyz(x+y+z),等价于

x3y+xy3+y3z+yz3+z3x+zx3≥2(xy)2+2(yz)2+2(zx)2,等价于

xy(x-y)2+yz(y-z)2+zx(z-x)2≥0,于是(*)获证.