数学思想方法在勾股定理单元中的应用
2019-04-13广东省佛山市南海区大沥镇许海初级中学528231潘秀贞
广东省佛山市南海区大沥镇许海初级中学(528231) 潘秀贞
勾股定理是数学中的一个悠久而重要的定理,在利用勾股定理解题时,常常涉及到一些常用的数学思想.掌握基本数学思想和方法能使数学更容易理解和记忆.勾股定理应用中所蕴含的思想方法能使复杂问题简单化.在教学中,我们必须充分重视数学思维的培养,并注意各种思维方式的应用,通过具体的,解决数学问题的独立探索和钻研,领会数学思维的规律和方法,提高数学思维的严密性、灵活性等思维品质,达到举一反三、概括迁移、融会贯通的效果.
一、数形结合的思想
数形结合的思想即在研究问题时把数和形结合考虑或者把问题的数量关系转化为图形的性质,或者把图形的性质转化为数量关系,从而使复杂的问题简单化,抽象问题具体化.
例1小华在距离东西向的高速公路500 米处观察,看见一辆轿车在高速公路上疾驰,30 秒后轿车到达B 点,他测得AB 的距离是1300 米,求轿车的速度.
分析根据题意,画出图形,其中点A 表示小华所在位置, 点C、点B 表示两个时刻轿车的位置.由于小华距离公路500 米, 因此∠C是直角,这样就可以由勾股定理来解决这个问题了.

图1
解在Rt△ABC 中,∠C =90°,由勾股定理,得AB2=BC2+AC2,故13002= BC2+5002,所以BC = 1200,轿车的速度为(米/秒),即为144 千米/时.
二、整体思想
有很多数学问题, 如果我们有意识地放大考察问题的“视角”, 往往能发现问题中隐含的某个“整体”, 利用这个“整体”对问题实施调节与转化,常常能使问题快速获解.象这种从整体观点出发,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题思想方法,称为整体思想方法.
例2如图2,已知Rt△ABC 的周长为其中斜边AB = 2,求这个三角形的面积.
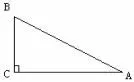
图2
分析若要直接求出a 与b 的值,要用二次方程求解较繁.但由联想到运用整体思想(将ab 视为一个整体)问题便可顺利获解.
解在Rt△ABC 中, 根据勾股定理, 得a2+b2= 22,即(a + b)2- 2ab = 4, 又由已知得所以所以ab=1,所以
三、方程思想
方程思想是指对所求问题通过列方程(组)求解的一种思维方法,中考中用方程思想求解的题目屡见不鲜.
例3如图3,矩形纸片ABCD中,AB =6cm,BC =8cm,现将其沿EF 对折使得点C 与点A 重合,求AF 的长.
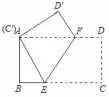
图3
解设AF =xcm,则DF =(8-x)cm,依题意折叠得D′F = DF = (8 - x)cm, D′A = DC =AB =6cm,∠D′=∠D =90°,在Rt△AD′F 中,由勾股定理得方程: 62+(8-x)2=x2,解得x=6.25,即AF =6.25cm.
四、分类思想
数学中的分类讨论就是把所研究的对象按可能出现的情况不重复无遗漏地分别加以讨论,从而获得完整的问题的解答.数学中的许多问题,只有用分类讨论的思想才能保证解答完整准确,做到“不漏不重”.
例4如图4,长方体的长为15,宽为10, 高为20, 点B 离点C 的距离是5, 一只蚂蚁如果要沿着长方体的表面从点A 爬到点B,需要爬行的最短路程是多少?
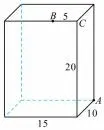
图4
解共有三种路线可走:
(1)把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形, 如图5: 因为长方体的宽为10,高为20,BC = 5,所以BD = CD+BC = 10+5 = 15,AD =20.在Rt△ABD 中,由勾股定理得:=25.
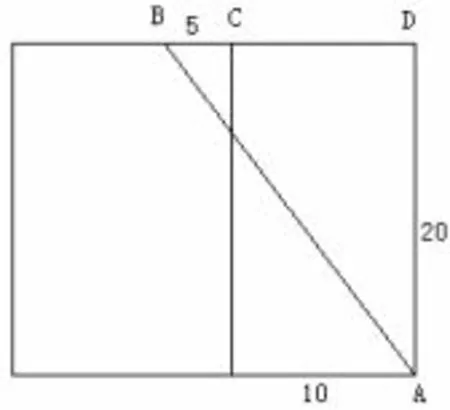
图5
(2)把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形, 如图6:因为长方体的宽为10,高为20,BC = 5,所以BD = CD+BC = 20+5 = 25,AD = 10.在Rt△ABD 中, 由勾股定理得:

图6
(3)把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形, 如图7: 因为长方体的宽为10, 高为20,BC =5,所以AC =CD+AD =20+10=30.在Rt△ABC中, 由勾股定理得:

图7
五、类比思想
类比思想是数学学习的重要发现式思维,它是一种学习方法,同时也是一种非常重要的创造性思维.它通过两个已知事物在某些方面所具有的共同属性,去推测这两个事物在其他方面也有相同或类似的属性.从而大胆猜想得到结论(必要时要加以证明)
例5(1)如图8,分别以直角三角形ABC 三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3.
(2)如图9,分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系? (不必证明).
(3)如图10,分别以直角三角形ABC 三边为边向外作三个等边三角形, 其面积分别用S1、S2、S3表示, 请你确定S1、S2、S3之间的关系并加以证明.
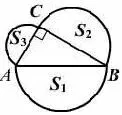
图8

图9
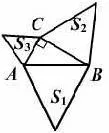
图10
分析从同学们熟悉的勾股定理入手,(1)(2)容易得证,(3)中要求出等边三角形的面积.
解 设直角三角形ABC 的三边BC、CA、AB 的长分别为a、b、c,则c2=a2+b2
(1)S1=S2+S3;
(2)S1=S2+S3;
六、转化的思想
原苏联数学家雅诺夫卡娅在回答“解题意味着什么? ”时说“解题就是意味着把所要解的题目转化为已经解过的问题.”可以说, 任何一个数学问题都是通过数或形的逐步转化,化归为一个比较熟悉、比较容易的问题,通过对新问题的解决,达到解决原问题的目的.可见,转化是解决数学问题的一种重要方法.数学解题的过程实际就是转化的过程,换言之,解题就是把所要解决的问题转化为已经熟悉的问题的过程,通过对条件的转化,结论的转化,使问题化难为易,化生为熟,最终求得问题的解决.
例6如图11 所示, 有一个圆柱,它的高等于12 厘米, 底面半径等于3厘米.在圆柱底面的A 点有一只蚂蚁,它想吃到上底面与A 点相对的B 点处的食物,沿圆柱侧面爬行的最短路程是多少? (π 的值取3)
分析在圆柱表面上蚂蚁爬行的路线是曲线, 其长度不易计算, 把圆柱沿经过点A 的母线剪开, 则爬行的最短路线是图中线段AB, 此时由勾股定理得.
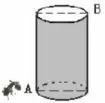
图11
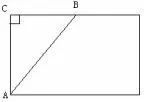
图12
点评立体图形上的问题常常要把它展开转化为平面图形问题.
在数学教学中,如果我们加强了数学基本思想方法的教学,并注重思维训练,可优化学生的思维,有助于学生能力的迁移,更能提高数学的教学质量.
数学思想方法已成为未来社会公民必须具备的数学素养中的核心内容.数学思想方法是随着学生对数学知识的学习、运用逐步形成的.数学思想方法是数学的生命和灵魂,是数学知识的精髓,是把知识转化为能力的桥梁.教师在平时教学中要让学生在学习中注意总结提炼,相互讨论,在解题的同时掌握有关的数学思想方法.
