解题反思四部曲,提升数学思维能力

广东省梅州市五华县田家炳中学(514400) 叶东辉

关键字 解题反思;解题能力;数学思维能力

著名数学教育家波利亚在“怎样解题”表中给出解题过程的四个步骤: 弄清问题——拟订计划——实施计划——回顾,其中的“回顾”即是数学问题解决过程中的反思.《普通高中数学课程标准》中也明确提出了“自主探索”、“反思构建”等与反思密切相关的目标和要求.解题反思是从一个新的角度,多层次对问题进行分析和思考,从而深化对问题的理解, 优化解题思路, 探索一般规律和通性通法, 归纳升华,促进知识的迁移,寻求新的发现.笔者认为通过以下“解题反思四部曲”不仅能提高学生的解题能力,同时达到提升学生数学思维能力和创新发展能力的目标.

一、解题反思第一部曲: 反思解题的思维过程、论证过程,提高数学思维的严谨性.

反思解题的数学思维过程包括分析、综合、比较、概括判断和推理等基本过程.反思解题过程,就是对整个解题过程进行全面的检查: 条件是否充分,转化是否等价,是否合乎逻辑,计算是否有误.如解应用题得到“需要0.8 个人”,求出面积、长度为负数等这样的结果,就不难判断出解题有误,需要检查列式或者计算是否有错或者某一步转化的条件不满足.

例1求函数的值域.

解题反思

提问1: 甲同学做对了吗? 同学们议论纷纷,有的认为对,有的认为不对.

提问2: 基本不等式在取等号的时候应注意什么?

同学们: 两个数相等时才能取等号.

师引导: 在学习基本不等式前,我们求函数的值域、最值用什么方法呢?

同学们: 利用函数的单调性.

例2设P 是双曲线上一点,F1、F2分别是双曲线左右两个焦点,若|PF1|=9,求|PF2|的长.

引导学生反思回顾, 就会发现错误的原因是忽略了题目中的隐蔽条件: |PF2|的长度最小值应为c-a = 2,所以|PF2|≥2,即|PF2|只能等于17.

通过对解题过程和结果的反思,发现解题过程中存在的问题,使学生加深了对基础知识、基本概念的理解,完善了解题的思维过程,更重要的是促进学生养成严格推理、论证的思维习惯,不随意套取公式、定理、结论武断地得出结果,克服思维的片面性,养成严谨缜密的思维品质.

二、解题反思第二部曲: 反思一题多解,激活思维,拓展解题途径和思维广度.

例3 已知定点C 的坐标是(2,2), 过点C 的直线CA与x 轴交于点A,过点C 且与直线CA 垂直的直线CB 与y轴交于B 点.设点M 是线段AB 的中点,求点M 的轨迹方程.

思路分析寻求动点M 满足的条件,并把条件转化为关于x,y 的等量关系,是解题的关键,注意到CB⊥CA,容易联想到两直线垂直时斜率的关系,对斜率不存在的情况补充说明.

解设M(x,y), 则A(2x,0), B(0,2y), 当x /= 1 时,因为CA⊥CB, 所以kCA· kCB= -1, 所 以化简得:x+y-2=0(*).又当x=1 时,CA⊥Ox 轴,得M(1,1),它满足(*)式.所以所求的轨迹方程是x+y-2=0.

解题反思上述解法应用平面解析几何中两直线垂直时斜率的关系解题.

引导思考1: 因为CA⊥CB,所以△ABC 是Rt△,斜边是AB,且M 是AB 的中点,同学们能联想到在Rt△中,斜边上的中线可建立的等量关系?

同学甲: Rt△斜边上的中线等于斜边的一半.

于是我们得到解法2:

解连结CM, 在Rt△ABC 中, M 是 斜边AB 的中点, 所以即化简得: x + y - 2 = 0, 所以所求的轨迹方程是x+y-2=0.

引导思考2: 垂直关系除了斜率之积等于-1,还可以建立什么等式?

同学乙: 在平面向量中,两向量垂直时它们的数量积为0,且可以省去对斜率的讨论!

解法3因为所以所以(2x-2,-2)·(-2,2y-2)= 0, 化简得: x + y - 2 = 0, 所以所求的轨迹方程是x+y-2=0.

通过对本题的一题多解,可以总结出几何中垂直关系可以考虑建立的多个等式,根据条件择优使用,达到快速剖析题意,建立方程的效果.本题还可以引导学生从垂直关系类比平行关系,总结平行关系所涉及的各种等量关系.

引导学生反思一题多解,点燃思维的火花,从多角度探寻解法,开拓思路,勾通知识,掌握规律,优化解法,在更多维度更高层次更富有创造性地去学习、摸索、总结,拓宽了解题的途径和思维的广度.

三、解题反思第三部曲: 反思多题一解,探求通性通法,提高归纳概括的数学思维能力.

在解题实践中,我们会经常遇到一些类似的、相近的题目,如果能够把它们放在一起进行分析、比较,就能发现题目和解题的方法存在某些的共同特点,从而可以探求出通性通法,在此基础上进行归纳、概括、提炼,然后再指导我们去解决的类似问题.发挥多题一解的优势, 使重要数学方法、公式、定理的应用规律化、条理化,那么学习能达到事半功倍的效果,思维也得到了提升和发展.

例4如图1, 点P 是△ABC 的外心, 且则=______.

思路分析本题的解法有很多种,比如可以利用特殊位置法,假设外心点P 在BC 上,然后利用两个向量数量积的定义就可求解.如果能把非垂直关系转化为垂直关系,利用数量积的几何意义,则能轻松解决.

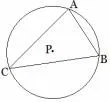
图1

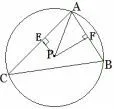
图2

解取弦AC 的中点E,弦AB 的中点F.则

例5如图3, O,A,B 是平面上的三点, 向量设P 为线段AB 的垂直平分线CP 上任意一点,向量若|a|=3,|b|=1,则p·(b-a)=( )

A.2 B.4 C.-2 D.-4

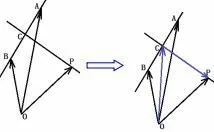
图3

思路分析利用“垂直平分”的特点,转化为数量积.因为所以=-4.

例6如图4,在△ABC 中,已知AB = 4,AC = 2,点H,O 分别是△ABC 的垂心和外心,则=____.

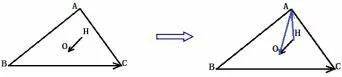
图4

思路分析连结AO、AH,则根据前例即可解得.

解题反思对以上三例进行反思,透过“现象”寻求“本质”,可以发现这类问题的共同解题思路是: 非垂直关系转化为垂直关系,垂直关系转化为数量积.多题一解,归纳概括出通性通法,不仅使解题能力实现从量到质的飞跃,而且使数学思维能力、创新能力得到提升和发展.

四、解题反思第四部曲:反思解题的数学思想方法,提高数学素养和思维品质.

数学思想方法是数学知识的高度抽象和概括,它蕴含在数学知识发生、发展和应用的过程中.恰当地运用数学思想方法能化抽象为直观、变繁杂为简易、转曲折为捷径,体现数学思想方法在解题中的强大威力.当学生能自觉运用数学思想方法去解决问题时,那么他的数学素养和思维品质就得到了很大提高.

例7求椭圆上的点到直线的最大距离.

解法一设直线x+2y+c=0与椭圆相切于点P,联立得:8y2+4cy+c2−16=0,由∆=16c2−4×8×(c2−16)=0,得:结合图形可知,当直线与该椭圆相切于点P时,点P到直线的距离最大,此距离等于两条平行直线与之间的距离,故

解法二设椭圆上任一点P的坐标为(4cosθ,2sinθ),则点P到直线的距离d=因为所以dmax=所以点P到直线的距离的最大值为

解题反思解法一对点P设而不求,把点P到直线的距离转化为两条平行直线之间的距离,体现了化归与转化和数形结合的数学思想方法.解法二利用了参数的数学思想方法,对于诸如动点P(x,y)的坐标关系不易找出时,可引入参数,三角换元,利用三角等价变形求最值.

反思研究问题所运用的思想方法,加深对数学思想方法的认识和理解,总结使用数学思想方法的规律和技巧,促进学生在解题时自觉应用数学思想方法,提高数学素养和思维品质,这也是数学教育的目的之一.

结语高中数学的学习中最关键的环节就是悟,是善于反思.如果学生在平时学习过程中获得正确答案就终止,不进行回顾和反思,那么学习就停留在经验水平,事倍功半;如果经常运用解题反思“四部曲”,总结成功的经验或失败的教训,不仅能有效加强对知识、技能的深化理解,而且有利于训练思维,促进知识向能力的转化,提高学习效率,促进学生的思维在更高的层次上概括、综合、融会贯通,进入理性认识阶段.