同图异构教学与培养学生发散思维能力的探究

广东省龙门县蓝田民族中学(516800) 邓继承

著名的心理学家吉尔福特指出:“人的创造力主要依靠发散思维,它是创造思维的主要部分.”发散思维对问题从不同角度进行探索,从不同层面进行分析,从正反两极进行比较,因而视野开阔,思维活跃,可以产生出大量的独特的新思想.发散性思维的特点是思维的积极性、求异性、广阔性、联想性等,在数学教学中有意识地抓住这些特性进行训练与培养,既可提高学生的逻辑思维能力,又是提高数学教学质量的重要一环.因此,在初中数学平面几何教学中,应加强对学生进行发散思维的培养.

一、运用命题的推广与延伸,提高学生的发散思维.

在教学过程中,要结合实际问题,运用命题的推广与延伸,也就是命题推广、答案延伸;或者命题条件不变,结论开放,利用同题异构的差异性,培养学生观察、联想的综合能力.要求学生能从观察、已知条件中,产生一系列联想,并从联想的结构中得出由条件产出的结论,再从多个结论中,选择有用的部分.运用命题的推广与延伸,只是要求学生选择发散性思维中有用的部分, 并且通过综合整理使问题得到解决.这样循环往复就能够培养学生的发散性思维.

下面结合一道小题谈一谈教学法的运用.

八年级上册《南方新课堂》(配人教版)第17 页习题2.如图1, AC = DB, AB = DC, 求证:△CAB△BDC.

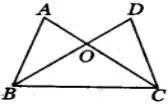
图1

证明由已知,AC =DB,AB =DC,BC =CB,所以△CAB△BDC (SSS).

在教学过程中,我们可以让命题条件不变,结论开放: 变出新题,以求达到触类旁通的效果,从而培养学生的发散思维,提高学生的认知能力.

变式1如图1,AC =DB,AB =DC,求证:∠A=∠D.

证明由已知,AC =DB,AB =DC,BC =CB,所以△CAB△BDC (SSS),所以∠A=∠D.

变式2如图1,AC =DB,AB =DC,求证: △ABO△DCO.

证明由已知, AC = DB, AB = DC, BC = CB,所以△CAB△BDC ( SSS ), 所以∠A = ∠D, 又∠AOB = ∠DOC,AB = DC, 所以△ABO△DCO(AAS).

变式3如图1, AC = DB, AB = DC, 求证: BO =CO.

证明由已知, AC = DB, AB = DC, BC = CB,所以△CAB△BDC ( SSS ), 所以∠A = ∠D, 又∠AOB = ∠DOC,AB = DC, 所以△ABO△DCO(AAS),所以BO =CO.

变式4如图1,AC = DB,AB = DC,求证: △OBC是等腰三角形.

证明由已知, AC = DB, AB = DC, BC = CB,所以△CAB△BDC ( SSS ), 所以∠A = ∠D, 又∠AOB = ∠DOC,AB = DC, 所以△ABO△DCO(AAS),所以BO =CO,所以△OBC 是等腰三角形.

点评上述变式题,其实是由图1 引导出来,条件一样,所要求的结论各不相同.但其实都要通过上面的证明来搭桥通过.这样的学习,要求学生能从观察、已知条件中,产生一系列发散性联想,并从联想的结构中得出由条件产出的结论,再从多个结论中,选择有用的部分.

结合八年级学生特点,在同样的条件下,引导学生从发散性思维中收拢,择选,归纳出有用的结论.这样的学习,循环往复就会使得学生的发散性思维得到提高.当然,中学数学的平面几何中,由于初中学生的年龄特点,学生思维发散的对象和方式是多种多样的,我们还可以让同样的一个命题推广、答案延伸, 在教学过程中, 不断激发学生的发散思维,提高学生的认知能力.

命题推广1如图2, O 为△ABC 内一点,BO 交于AC 于E,CO 交于AB 于D, BD = CE, 且BE =CD,求证: AB =AC.

图2

证明由已知,BD =CE,且BE= CD, BC = BC, 所以△CDB△BEC ( SSS ), 所以∠BDC = ∠CEB, 那么, ∠ADC = ∠AEB.又∠A = ∠A,BE =CD,所以△ADO△AEB(AAS),所以AB =AC.

当然,上题解法很多.参考变式题,可以有多种解法.像这样的题目,基础知识容量大,由浅入深地沟通了各章节之间的知识与方法的内在联系.在平时的训练中,多做这些题目,有利于全面系统地巩固基础知识,提高解题能力,培养发散思维的灵活性.

二、运用问题条件的减弱和加强,提高学生的发散思维.

人的逻辑思维能力,不是一朝一夕形成的,需要在长期反复练习的过程中逐步提高.而初中学生十几岁时正是培养这种能力的最佳时期,人一生中的许多能力和习惯都是在那个时候形成并且终生难改.回到同时期数学教学上,我们可以对于同一个数学问题,引导学生积极思考,深入探索,对问题的条件多思多疑,敢于质疑,改变条件,结论不变,变出新题,会达到触类旁通的效果,从而培养学生的发散思维,提高学生的认知能力.

例子求证: 等腰三角形两底角的平分线交点到底边的两端点距离相等.(如图7)

已 知: 如 图3, 在△ABC 中,AB = AC,BD、CE 分别是∠ABC、∠ACB 的平分线,且BD、CE 相交于点O,求证: OB =OC.

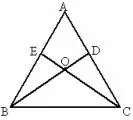
图3

证明因为AB = AC, 所以∠ABC = ∠ACB.又因为所以∠OBC =∠OCB,所以OB =OC.

例5如图4, 在等腰三角形ABC 中,AB =AC,BD、CE 分别是中线,且交于点O,求证: OB =OC.

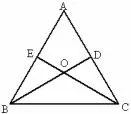
图4

证明因为所以BE =CD.又因为∠ABC=∠ACB,BC 为公共边, 所以△DCB△EBC, 所以∠DBC = ∠ECB, 所以OB =OC.

例6如图5,在等腰△ABC 中,AB = AC,BD、CE 分别是高且交于点O,求证OB =OC.

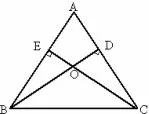
图5

证明在Rt△BCD,Rt△CBE 中,因 为 ∠EBC = ∠DCB, BC 为 公 共 边, 所 以Rt△BCDRt△CBE,所以∠DBC =∠ECB,所以OB =OC.

上述例题题,其实是由图3 引导出来,结论一样,所要求的条件各不相同.对同一问题从不同的角度去分析,结合不同年级的知识水平,鼓励学生以问题条件为出发点,鼓励学生关注基础,但不落俗套,追求尽可能与众不同的解题思路和解题方法,有利于全面系统地巩固基础知识,提高解题能力,培养发散思维的灵活性

命题推广2如图6, 在△ABC 中, AB = AC, BD、CE 分别是∠ABC、∠ACB 的平分线, 且BD、CE 相交于点求证: ∠A=60°.

证明(略.由等腰三角形的性质,结合条件和△BEC△CDB 可得.)

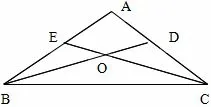
图6

三、开放条件和结论,启发求异,培养学生的发散思维.

求异思维是创新思维的核心,是培养学生创新能力的关键.教师教学时,要启发学生从不同的角度,不同的方向去思考问题.有目的的鼓励学生开放题目的条件和结论,标新立异,不落俗套,追求尽可能与众不同的解题思路和解题方法.教师还要注意引导学生将发散思维与聚合思维综合运用,运用发散寻求更多的解决问题的方案,然后再用聚合思维在多种方案或方法中选择出一种合理、最简便的解决方案.

例子如图7,已知AD 是△ABC的中线, DE⊥AB 于E, DF⊥AC 于F,且BE =CF.

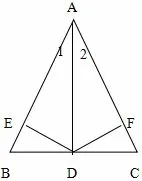
图7

求证: (1)AD 是∠BAC 的平分线;

(2)AB =AC.

证明(1)由已知,AD 是△ABC的中线, 所以BD = CD.因为DE⊥AB 于E, DF⊥AC于F, 所以∠BED = ∠CFD = 90°, 且BE = CF, 所以△DEB△DFC (SAS), 所以DE = DF, ∠BED =∠CFD, AD = AD, 所以△AED△AFD (HL), 所以∠1=∠2,所以AD 是∠BAC 的平分线.

在教学过程中,我们可以开放题目的条件,结论,启发学生从不同的角度,不同的方向去思考问题.

变式题如图8, DE⊥AB,DF⊥AC, 垂足分别为E、F, 请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题.①AB = AC; ②BD =CD; ③BE =CF.

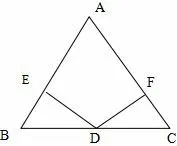
图8

明显地,变式题是由例题变化得来.这样有目的的鼓励学生开放题目的条件和结论,标新立异,不落俗套,追求尽可能与众不同的解题思路和解题方法.例如,由 ①AB = AC,②BD = CD 作为条件得到结论 ③BE = CF; 由 ③BE =CF, ②BD =CD 作为条件得到结论 ①AB =AC;由 ①AB = AC, ③BE = CF 作为条件得到结论 ②BD =CD.

这样,开放性的鼓励学生自由组合,自行解决问题.有效的培养了学生的创新能力,锻炼了学生的逻辑思维能力.

总的说来,一个表意完整的平面几何题目通常由语言符号和图形符号共同组成,在我们的感官中,视觉产生的效果是最直观也是最容易留下深刻印象的.在初中数学的课堂教学中,一道寓意丰富,深刻、精美的画形可能比一篇长文更受欢迎.图像诉诸情感,而文字具有确定性和逻辑性,两者相辅相成,作用于学生的思维逻辑生成,能够帮助学生更加准确地理解数学学习的作用和意义.

在平面几何的教学中,有意识地同图异构,在同一个图形中条件不变要求推导出多种结论;或者,在同一个图形中条件多变要求推导出共同的结论,这样就沟通了各种知识的内在联系,使已学知识成系统;同样地,在同一个图形中,创造出种种情景,即可培养学生的观察、联想习惯,又利于激发学生的学习兴趣,还可帮助学生克服某种思维的定势,丰富学生分析时的指向,提高发散思维的流畅性,从而锻炼,培养了学生的发散思维能力.