合理运用好微课,改善几何教与学*

2019-04-13广东省广州市聚德中学510305林彩满

中学数学研究(广东) 2019年6期

广东省广州市聚德中学(510305) 林彩满

前言

《数学课程标准》指出:“数学课程的设计与实施应重视运用现代信息技术……大力开发并向学生提供更为丰富的学习资源,把现代信息技术作为学生学习数学和解决问题的强有力工具,致力于改变学生的学习方式……”教学改革的全面展开和信息技术的深入应用,催化了课堂教学模式的变革.”越来越多的智慧课堂,翻转课堂,洋葱数学等微课形式的资源被越来越多的教师所提起,广州市11 月的教研活动的主题就是“信息技术与教学的融合”.微课运用将会越来越普遍.

一、好的微课资源能有效降低教学难点

1.上好“将军饮马”有难度

“将军饮马”问题是人教版数学八年级上册第85 页,13.4课题学习“最短路径问题”中的内容.它出现在轴对称图形这一章,因为它用了作一点关于一条直线的对称点,用到轴对称图形的性质: 对称点的连线被对称轴垂直平分,从而实现线段的转化.这是一个节较难开展的活动课.原因有两个: 首先,在解释为什么这么做时,教师往往觉得很生硬,不够自然.其次,证明方法少见: 取另一个点,用三边关系证明为什么作对称找到的点满足距离最短的条件.很多学生特别是基础薄弱的学生往往有两个表现,第一,线较多,找不到三角形,不容易发现;第二,听懂,能模仿着画出来,知其然不知其所以然.

2.我的教法实践: 黑板+粉笔的传统模式

在过去的教学中,我的上课程序主要有以下几步:

(1)先让学生回忆有关线段最短的知识点: 两点之间线段最短(点与点),点到直线的所有连线中,垂线段最短(点与线);

(2)两点在直线的异侧(学生在这个环节能很快完成);

(3)两点在同侧,让学生先画图.受到前面知识的影响,学生往往在画图时只关注到其中一段线段是最短的情况,例如图1(过一点向直线画垂线,垂足与另外一点的连线)又或者受刚刚学到的线段垂直平分线的影响,画出两点连线的垂直平分线,该线与直线的交点(如图2),学生就以为是所求的满足最短距离的点;

图1

图2

(4)我提供作对称的方法,让他们用测量的方法,比较作对称的方法与自己做法的比较,看哪个距离短;

(5)解释为什么这样找的点是满足条件的.另选一点,用三边关系证明.在这种教学方法下,往往出现的现象是: 有学生在画图环节耗费较多时间,作图效果也很不一样,想通过测量探究环节让学生理解的想法往往落实不了.

3.传统教学遇见微课

2018年11 月23 日在广大附中的广州市教研活动中,赖巧芳老师用洋葱数学中的微课,用技术解决一支粉笔解决不了的问题,洋葱数学的微课构建生动的教学情景,在关键处暂停视频3 次: ,暂停1: 转化为A 的对称点与B 的连线中,哪一条最短的问题, 暂停2: 如何证明最短; 暂停3: 证完最短,用几何画板展示垂线段,中垂线画法的路线为折线.赖老师的教法给使用微课教学的老师一个很好的示范,信息技术能呈现抽象对象的直观背景,可以不打断原有教学节奏,在关键的理解点插播,在难点处暂停.将军饮马问题单从老师的描述或课本的文字,不够形象,加入洋葱微课,不仅仅能调动学生的积极性,很快融入情景,而且,洋葱老师的细致讲解,很好地加深了学生对画对称点原因的理解.《义务教育数学课标准》指出:“有效的数学教学活动是学生学与教师教的统一,学生是数学学习的主体,教师是数学学习的组织者、引导者与合作者.”这节课上,微课的有效使用,很好地体现了这一理念.

二、教师开发微课可以提高讲题质量

数学课堂,讲题是数学课堂很重要的组成部分,特别是初三复习阶段,评讲题目是家常便饭.在评讲一道相对于班级学生水平有较高难度的几何题目时,例如近几年广州市中考的第16 题,是一种一图多问型几何题目,如果采取黑板+粉笔的形式,往往会出现的现象: 部分学生跟不上,因为这类题目上一个结论会对后面的证明有影响,如果一个结论听不懂,跟不上,学生往往会出现假听课的现象.表面在听,但没懂.教师在黑板上讲时,往往讲得很投入,以为学生听懂了.黑板上的图形往往会多次被描,结果是线段与角的信息很花,很乱,看不清.笔者曾经调查过这样讲评,下次小测类似知识点,47 人的班级,不到三分之一的学生能做对.要达到“人人都能获得良好的数学教育,不同的人在解决数学问题的能力得到不同的发展,在解决数学问题的能力上得到不同的发展.”教师就得因材施教,让学生有多一个选择的机会.教师自己制作微课,就是一个会提高学生的听课效率,能利于学生能力发展的方法.

1.我的实践: 以退为进的微课教学设计

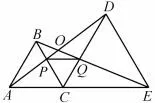
图3

题目如图3, C 为线段AE 上一动点(C 不与点A,E 重合), 在AE 同侧分别作正三角形△ABC 和正三角形△DCE,AD 与BE 交于点O,AD 与BC 交于点P, BE 与CD 交于点Q,连接PQ.有下列结论: ①AD = BE; ②AP = BQ; ③∠AOB = 60°;④DE = DP; ⑤△CPQ 为正三角形.其中正确的结论有____.

A.①②③⑤ B.①③④⑤ C.①②⑤ D.②③④

(1)微课视频画面1: 如右图, 两个等边三角形: △ABE与△DEC,边BE 与边EC 在同一直线上.请思考: 有哪些角是特殊度数,哪些线段相等?(设计目的: 让学生复习等边三角形的有关角的性质及条件中在同一直线上所隐含的有关角的信息)

图4

(2)微课视频画面2: 如右图,比上一个图增加两条线, 图中的三角形变多.你能发现哪个三角形与△BED 全等? 前面的哪些结论要用到?

图5

(3)微课视频画面3: 如右图,证明△FED 和△PEC 全等,用到之前证明△AEC△BED的哪些结论?

图6

(4)微课视频画面4: 如右图,请判断△FEP 的形状,用到之前的什么结论?

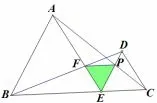
图7

图8

(5)微课视频画面5: 小结,学法指导.这道题是两个有公共顶点的等边三角形, 其中一边在同一条直线上.在连接另外两个顶点后,产生了两对全等三角形,一个特殊三角形.此类问题特点: 线不断增加,可以先从最简单的图形开始画起,考虑问题时从角,线段,三角形全等三方面来考察.上述录制微课的方法还可以尝试通过学生4 人小组讲题时真人录制,这样,课后使用微课的学生看起来会更有亲切感,更能引起共鸣.