基于大数据下初中数学错题的应用研究*

广州市增城区石滩镇三江第一中学(511325) 陈桂玲

一、问题的提出

教了十几年的初中数学,我们总是发现,某一道数学题讲过了,做过了,甚至考过了,下次再做时,仍然会有三分之二学生出错.于是初中数学教师总是很无奈地叹声说:“这些数学题目我已经重点评讲了,而且帮助学生找到错误的根源,让学生及时改正了,为什么进行单元测试时,至少三分之二的学生还是做错呢? ”有的学生很冤枉地说:“当我第一次做错时,我就很认真听老师分析、讲解,当时也学会了,而且立刻改正过来了,可是不知道为什么,当隔了一段时间再做时,我一点印象都没有了,又不会了.”有的学生很烦恼地说:“做错的数学原题,我是会做了,但如果题目更改一些条件,那我就不会做了.”学生委屈地说“我已经很努力学习数学了,而且做了大量的题目,为什么我的数学成绩还是上不去呢? ”

二、原因分析

初中学生的数学成绩上不去, 做错的数学题一错再错,或者对数学错题不类触类旁通,其根源就是没有好好地在错题上反思,而是盲目地追求题海战术.这就像一个病人没有找到病根,就乱吃药,那只能病得更历害.

杜威曾指出:“失败并不是单纯的失败,也是一种教训.”[1]错题是一种为学习者量身定做的学习资源.真正善于思维的人,从错题中学到的东西和从成功中学到的是相等的.特级教师王金战曾告诫学生:“错题千万别放过.每个错题背后都隐藏着知识的遗漏;教师和学生都需要高度重视.”[2]有一个专家也说过,“做十道题,不如做一道错题”.

但是,收集错题并没有得到学生的重视,统计结果显示:有54.2%的学生对错题置之不理;20.7%会整理和翻看错题;67.7%因老师不要求就不整理错题.可见,对待错题,学生的主动性较差.“学生对于错题的态度受到教师的影响,教师的指导性没有完全体现出来,对错题的价值缺乏充分认识.”[3]错题没有很好地得到学生重视原因是: 第一收集错题困难.收集错题要求学生把在平时学习过程中做错的题目工工整整地抄下来,并完成地做出正确的答案,需要很多时间,可是学生每天的作业已经很多,他们难以抽出大量的时间把错的题目抄下来;第二不会写错误的原因.在学生总结出错原因的时候,学生也只会简单地写诸如“马虎”“粗心”“没有复习好”“试题出偏了”等这类似是而非的理由,不会真正反思自己出错的原因;第三对错题没有分类整理,或者说不会按知识点进行分类,导致错题本利用效率不高.在这种情况下,要么怕累,抽不出时间等原因没有收集错题;要么收集错题也只是形式而已,发挥不到错题的真正价值.

三、初中数学错题的应用研究

即使部分学生坚持做到“发现问题——归类错集——分析错题——反思错题”.但错题来源面狭,局限性大,没有收集到很好的典型错题,导致利用错题的效果不高.

根据人工收集错题的困难与效果不理想等情况,商家适时推出了一系列的APP,如神算子,一起作业网等等,学生在APP 在做数学题,然后APP 会根据学生做过的题,进行大数据的整理、分析、归类等,有效地建立错题集.“大数据,是指以多元形式,许多来源搜集而来的笼大数据组,能对数据组进行加工,通过加工实现数据的增值.大数据是不用随机分析法这样的捷径,而采用所有的数据进行分析处理.所以它具有大量,高速,多样,价值真实性四个特点.”[4]

借助这样的APP,收集初中学生的数学错题,具有数据题量巨大、数据类型繁多、价值密度低、处理速度快的四个特点.

为了发挥错题的最大用处,取得更好的学习效率,我们要把焦点放在通过大数据筛选出的那些高频错题分析研究上,从教师本身和学生两方面入手进行分析.对错题进行反思,探索行之有效,便于操作的错题防范措施,帮助学生走出困惑,走出错题.

(一)教师巧用错题资料,提高教学效率

1.课堂讲解,防范措施

教师根据大数据筛选出学生典型的、常考的错题,知道全班学生哪个知识点没有掌握好, 然后在课前从数学知识,数学教育心理(如认知结构,知识,经验,技能,态度等)方面对学生进行错题的成因分析.例如: 在人教版七年级数学上册,解一元一次方程:

学生主要错误有:

(1)方程的右边没有乘以6,如3(x-2)-2(2x+3)=1;

(2)去分母时,分子没有添加括号,如3x-2-2×2x+3=6;

(3)去括号没有变号,如3x-6-4x+6=6.

为了避免学生做错,教师上课前对错题不断地进行针对性分析、总结,在课堂授课时,教师可以有效地对易错的知识点进行加强.教师做好了易错题的防范措施,改进了教学方法,从而大大提高的教学效率.

2.个对性辅导、错题通关

有了大数据的支持,教师能准确知道每个学生的问题所在.使个性化辅导成为了可能.例如: 代数式有意义时,实数x 的取值范围是____.

学生的主要错误有:

(1)以为开方数不能为0,如填x/=9,x ＜9;

(2)被开方数错误,如填x ≥0;

(3)不等式变形掌握不扎实,两边同时去掉负号时没有改变不等号的方向,如填x ≥9.

教师根据学生的错题,发现每个学生的问题所在.及时帮助每个学生矫正错题, 个性化地弥补相关的数学知识点,这是保证每个学生在错题通关的最为直接和有效的途径.个性化辅导能大大提升学生的学习能力.

(二)学生重用错题资料,提高学习效率

1.对错题进行归因分析

利用大数据,可以整理出常考的、典型的错题,并把错题按某个或多个知识进行分类.例如: 分解因式2mx+6my.

学生的主要错误有:

(1)公因式提取不完全: 如m(2x+6y),2(mx+3my);

(3)似懂非懂.如2my.

学生在数学错题资源中比较、归纳、反思.在这成因分析过程中,学生不但能找出“病根”,还能建构出知识框架,弥补不足,升华相关的数学知识点,总结出相关解题思路与方法,从而提高学生的思维力和解题能力,增强了学生学习数学的自信心,那么数学成绩的提高就是顺水推舟了.

2.错题重做,触类旁通

大量类似错题的改正是数学错题学习法最重要的环节,关键是真正“改会”,是锤炼学生稳定发挥能力的过程.大数据能根据学生做错的题目,用类似的知识点筛选相应的变式题,重新检验学生的学习成果.

例题1如图1,在Rt△ABC 中,∠BAD = 90°, AB = AC.求证:AC2+AD2=BD2.

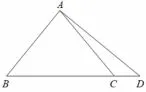
图1

在图形上求线段的关系中, 学生经常做错或无从入手,教师通过讲解求线段的数量关系的方法: 通过作辅助线或旋转的方法,构造一个直角三角形,然后利用勾股定理就可以求出线段的数量关系了.

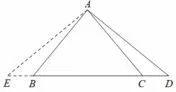
图2

如上题的例题1, 延长CB 到E, 使BE = CD, 连接AE, 如图2, 很容易证得△AEB△ADC, 得到AE =AD,∠DAC = ∠EAB,从而得到∠BAD = ∠EAC = 90°,所以AC2+ AE2= CE2.因为BD = CE, 从而证得:AC2+AE2=BD2.

学生重做错题后,再来做变式题,如2016年广州中考数学试题的第25 题:

如图3,点C 为△ABD 的外接圆上的一动点(点C 不在弧BAD上,且不与点B,D 重合),∠ACB =∠ABD =45°.

图3

(1)求证: BD 是该外接圆的直径;

(3)若△ABC 关于直线AB 的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.

学生通过重做错题, 掌握求线段的数量关系的方法后, 通过作辅助线或旋转的方法, 构造一个直角三角形,然后利用勾股定理就可以求出线段的数量关系了, 本题的第(2)问, 延长BE, 使BE = CD, 连接AE, 就能证得△AEB△ACD, 构造△AEC 为直角三角形, 且∠EAC = 90°, 如图4, 再利用股定理即可证得BC+CD;对于第(3)问,将△ADM 绕点A 旋转90°,得到△ABF 证得∠BMF = 90°如图5,BM2+MF2= BF2,从而证得DM2,AM2,BM2三者之间满足的等量关系是:DM2=2AM2+BM2.

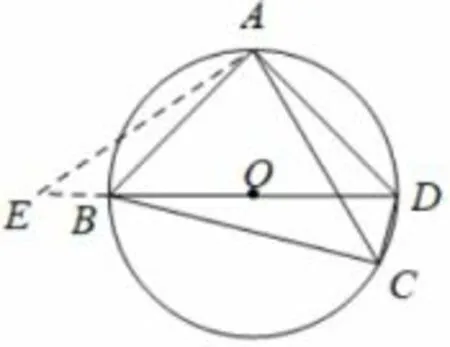
图4

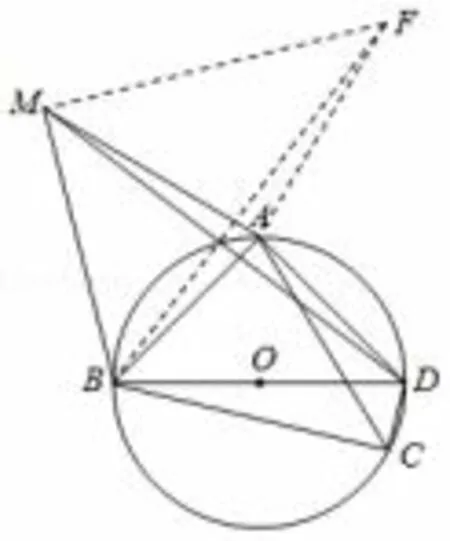
图5

学生通过重做错题,多做变式的错题.“在扩展上深刻理解,反思到原始错题的根源和知识点后,就会进一步向解题思路、数学思维方面倾斜,从而建立了这种知识点与题目的正确联系,那么数学的思想方法、基本知识和技能能得到进一步的提升,学生对类似题目就能触类旁通了.”[5]

如: 2018年广州中考数学试题的第25 题

如图6, 在四边形ABCD 中, ∠B = 60°, ∠D = 30°,AB =BC.

(1)求∠A+∠C 的度数.

(2)连接BD,探究AD,BD,CD 三者之间的数量关系,并说明理由.

(3)若AB = 1,点E 在四边形ABCD 内部运动,且满足AE2=BE2+CE2,求点E 运动路径的长度.

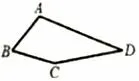
图6

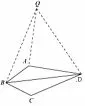
图7

对于第(2)问,学生能将△BCD 绕点B 逆时针旋转60°,得到△BAQ,连接DQ,如图7,∠DAQ = 90°,很容易得到AD,BD,CD 三者之间的数量关系是: AD2+CD2=BD2.

总之,学生需积极面对错题,分析错题,并在错题相关的知识点上进行归纳整理,随时翻阅和总结反思,按照原题-相似题-改编题-拓展题的方式梳理,是提高数学成绩和学习效益的重要捷径.

错题有着独特的价值,利用大数据,不断将错题回炉淬炼,一方面,教师把收集到的错题资源,进行归因分析,然后在课堂有针对性地讲解,避免学生做错起到防范作用,提高教师的课堂效率;另一方面,学生在纠正数学错题中,不断地弥补知识点,在变式的数学错题上反复练习,寻求不同的解题途径与方法,并进行不断地总结与提炼,从而掌握掌握全面而准确的分析问题,解决问题的能力.因此,在大数据时代,利用好错题,无论在教师的有效性教学,还是学生提高成绩方面,都能达到事半功倍的效果.