基于多普勒频谱的建筑物与植被场景分类技术

柴晓飞 罗丁利 徐丹蕾 杨 磊

(西安电子工程研究所 西安 710100)

0 引言

建筑物与植被作为雷达地杂波背景中的主要组成部分，对两者的识别和分类，可以帮助我们建立地区的场景先验信息，根据不同的杂波类型采用不同的杂波抑制方法，同时为阵地适配提供参考信息。目前基于合成孔径雷达图像的分割技术已经有较多的研究成果[1-5]，如基于数据驱动、模型驱动的SAR图像分割技术，这里主要针对低分辨雷达的频谱进行研究。

在有风的条件下，植被会出现缓慢的摇摆，由于杂波之间运动的随机性，目标频谱将会被展宽，即与固定建筑物的频谱会产生差异。二者有以下区别：

1)在同一部雷达的照射下，虽然影响地杂波的有很多因素，但建筑物的回波强度一般大于植被的回波强度。

2)建筑物的分布范围独立且集中，植被覆盖率高，分布范围宽广。

3)在有风条件下，植被受风作用摆动将产生随机多普勒分量，造成杂波谱展宽。而建筑物受风的影响小，频谱宽度小。

4)植被的运动还有其自身的特点，如双向交错性，短时间性，即在小段时间内，植被起伏大，平稳性差，而建筑物几乎没有任何波动。

该实验以某雷达为实验平台，采集杂波数据，来进行实验方法研究以及实验数据的验证。

1 地杂波频谱

在有风条件下，由于树木的摆动，产生多普勒分布，从而会展宽杂波谱的谱线，由于杂波源之间运动的随机性，经查阅文献[6]及雷达实测数据证明，指数分布最适合对风吹植被所形成的地杂波进行建模。

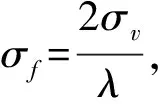
(1)

3dB谱宽可用标准差表示为：

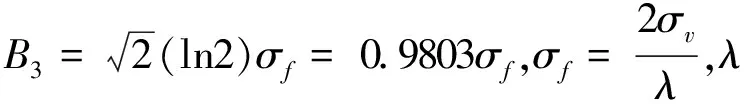
来自森林区域不同风速时地杂波频谱扩展的估计值见表1[7]。

表1 不同风速时频谱扩展的测量值

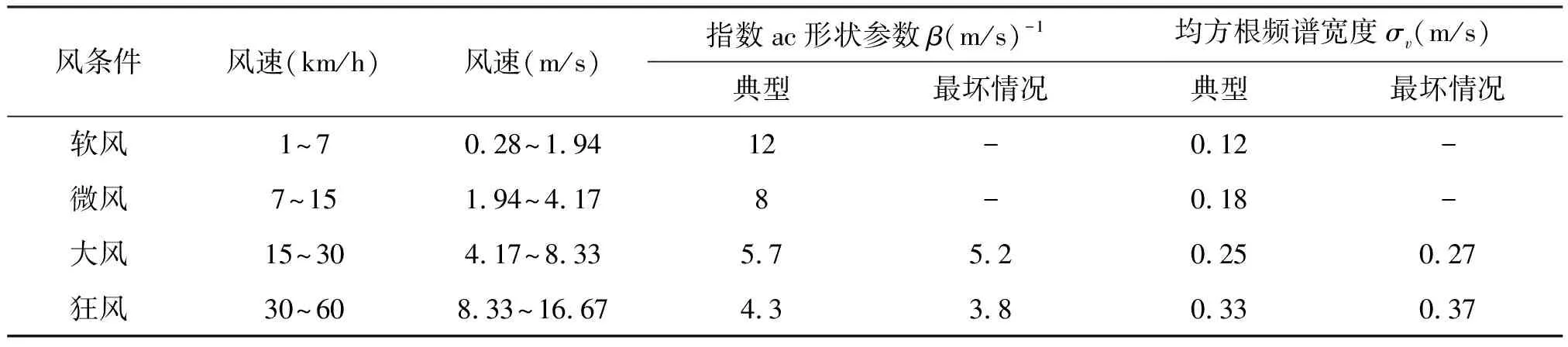
风条件风速(km/h)风速(m/s)指数ac形状参数β(m/s)-1均方根频谱宽度σv(m/s)典型最坏情况典型最坏情况软风1～70.28～1.9412-0.12-微风7～151.94～4.178-0.18-大风15～304.17～8.335.75.20.250.27狂风30～608.33～16.674.33.80.330.37

本文的所有数据来源于某雷达实验平台。该雷达平台静止工作，地杂波分布在零多普勒频率附近，主要探测地面活动的目标，用于警戒、侦察人员、车辆等动目标，测定其方位、距离和活动路线。

2 场景分类处理流程

处理机对接收到的雷达中频回波信号，利用数字下变频技术，将回波信号中承载的信息变化到基带，通过数字脉冲压缩技术，获得最大信噪比的输出信号，然后对脉压处理后的每一个距离单元内的慢时间序列做离散傅里叶变换(DFT)，得到相应的脉冲-多普勒平面。由于本文的研究对象是地杂波，因此可将地杂波视为期望信号进行检测，为了在干扰噪声功率电平变化的条件下保持CFAR，此处在多普勒维采用单元平均CFAR分析，得到检测后的数据矩阵，根据风速的大小和多普勒分辨率选取杂波单元，提取相应杂波单元内的频谱特征，送入训练好的分类器模型，进行场景分类，通过投票融合方法，进一步提高识别的准确度。场景分类处理流程如图1所示：

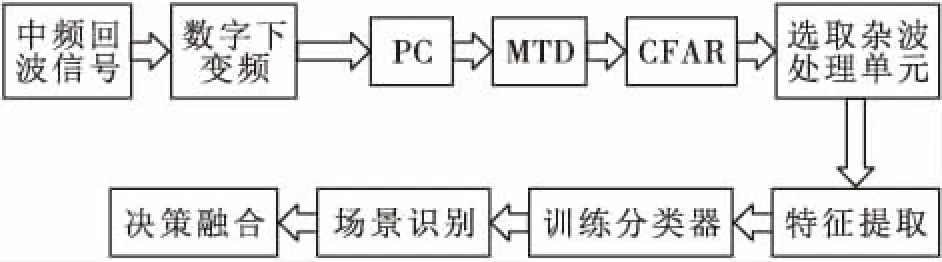
图1 场景分类处理流程图

2.1 选取杂波单元

地杂波处于零多普勒通道附近，由风速等级及多普勒速度分辨率可对植被杂波谱的展宽做出估计，确定所占多普勒通道数的最大区间，对经过恒虚警检测后的每个快时间-慢时间矩阵，在慢时间维截取对应多普勒区间数据，作为杂波单元。

2.2 场景识别

通过对该地区雷达扫描范围内的回波数据进行分析，可得到连续时间内对该地区的多次扫描结果，即基于不同时段的该地区样本值的强度和频谱进行研究。首先根据统计设定一个合适的强度阈值，对低于阈值的距离单元不做识别，直接判为未知目标。然后对强度高于阈值的距离单元，提取对应的杂波单元内的频谱特征，送入训练好的分类器模型，进一步对植被和建筑物进行识别分类。得到该地区不同时间段的多次识别分类结果。

2.3 决策融合

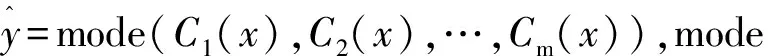
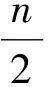
(2)

如图2，基于对该地区17次预测分类的情况下，单次决策结果错误率与集成学习错误率的关系曲线，交点大约位于0.5，即当单次决策结果的错误率小于0.5时，集成学习的错误率要低于单次决策结果；当单次决策结果的错误率大于等于0.5时，集成学习的错误率要高于单次决策结果。

该融合方法的优点是：不需要进行训练，简单有效；但是它也存在一定的局限性，即忽略了每次扫描结果的差异性，给予它们相同的输出同等地位；其次，容易出现相同票数的情况，需要拒判。

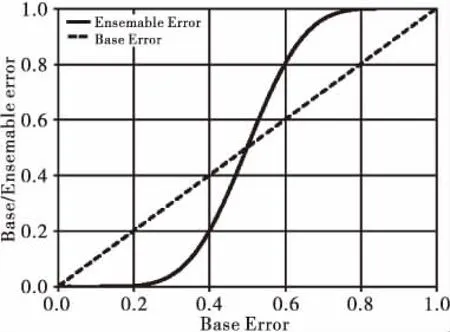
图2 单次决策错误率与集成学习错误率关系曲线

3 基于实测数据的目标特性选择与提取

为了说明该方法的可行性，专门选择一块实验区域，此处树木茂盛，农业主要种植小麦与玉米；建筑物分布范围小但大多数集中分布，多是低矮的房屋；且区域内还有部分的裸露地。

数据是在微风条件下采集的，区分两类目标主要是利用它们在有风条件下速度的差别，多普勒存在差异，杂波频谱展宽程度不同，反映在雷达距离-多普勒平面上即为两类目标占据多普勒单元的多少。如图3所示：

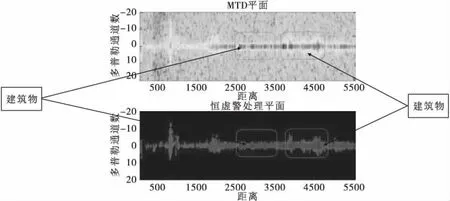
图3 距离多普勒平面

3.1 植被与建筑物频谱特征

从实测回波数据中，选取两类样本在有风条件的典型频谱。由于在有风条件下，草木会随风摆动，而且根据风向的不同，风速的不同，摆动幅度不同，目标频谱也会产生差异。即植被频谱相对于杂波谱中心并不总是对称的，频谱展宽起伏大且平稳性差，如图4所示。在有风条件下，建筑物的稳定性比较好，不会随着风速的变化而变化，因此目标的频谱呈箭状，分布在0多普勒通道两侧，有固定的杂波谱宽度，频谱相对于杂波谱中心对称，几乎没有起伏变化，如图5所示。

3.2 特征提取

由雷达参数可知，多普勒分辨单元为0.14m/s，此时风速等级大致为1～7km/h，对经过恒虚警检测后频谱所占的多普勒通道数的最大区间作出估计，即取0通道附近左右各10个作为杂波处理单元。

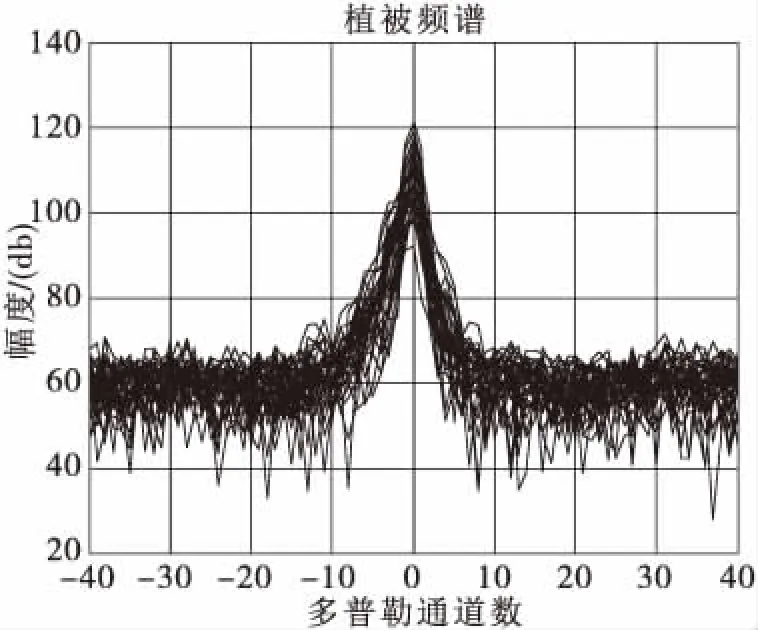
图4 植被频谱

图5 建筑物频谱

根据两类目标频谱特征的明显差异，对植被和建筑物各500个样本提取二阶中心矩、波形熵、频域归一化方差3个特征，并画出相应的分布直方图。从图中可看出两类目标有明显的差异，植被的频谱特征二阶矩大、波形熵大、幅度方差小；建筑物的频谱特征为二阶矩小、波形熵小，能量集中，幅度方差大。因此所提特征能够很好地区分植被和建筑物两类目标。

目标的多普勒谱X=[X(1),X(2),…,X(N)]，其中N为脉冲积累数。设X(n)出现的概率为P(n)。

(3)

3.2.1 二阶中心矩

二阶中心矩(后面简称二阶矩)是一种平移、旋转和尺度不变特征，可用来反映两类目标的形状信息。二阶矩计算公式表示为：

(4)

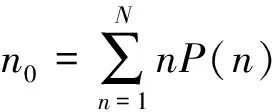
图6 二阶矩分布直方图

3.2.2 波形熵

波形熵(后面简称熵)是用来描述信源的平均不确定性。用频域波形熵来表征频域能量的散布程度，能量越集中，熵值越小。即熵值也用来作为识别两类目标的特征之一。

(5)

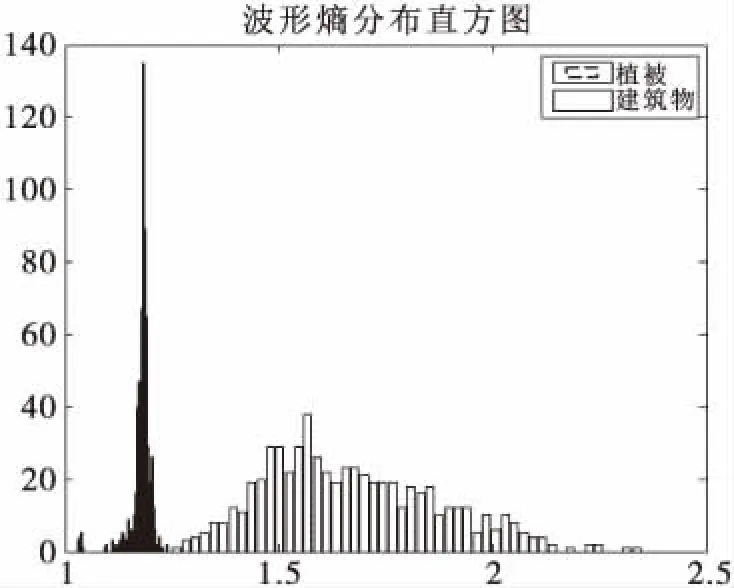
图7 波形熵分布直方图

3.2.3 频域幅度归一化方差

植被和建筑物两类目标频谱的幅度差异较大，故可提取各自频谱的方差作为识别的特征之一。由于存在幅度敏感性，将幅度取模值然后进行归一化处理。方差的一般定义为：

(6)

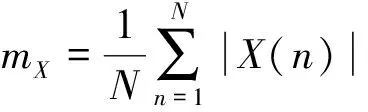
归一化方差为：

(7)

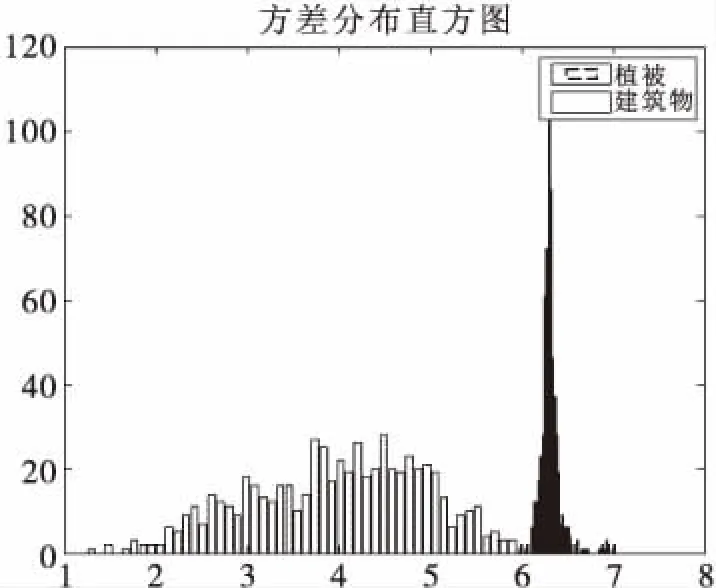
图8 幅度方差分布直方图

4 决策融合

4.1 支持向量机

本文通过对某地区有风条件下的地杂波谱提取的二阶矩、波形熵、幅度方差3个特征，采用支持向量机[8]对植被和建筑物的分布情况进行识别分类，验证所提特征都是有效且稳健的。

支持向量机(Support Vector Machine，SVM)是90年代初发展起来的一种监督学习的模式识别技术，对每个类别的已知样本值进行学习，进而对未知的样本进行预测。基本思想为：通过非线性变换将输入空间变换到一个高维空间，在这个空间里构造出不同类之间达到最大分类间隔的最优超平面即最大间隔分类面，而这种非线性变换是通过定义适当的内积核函数实现的。在基于低分辨雷达回波数据信噪比低，训练样本数较少的情况下，SVM能够得到比其它算法较好的结果，是因为SVM是基于结构风险最小化原则而不是经验风险最小化，这样就可以避免过学习的问题，计算复杂度小，泛化能力要比其它算法好。

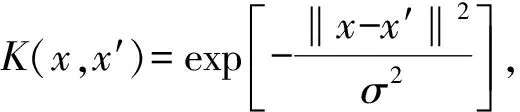
4.2 场景识别

选取典型植被频谱的样本500个，建筑物频谱的样本500个，分别提取二阶矩、幅度方差、波形熵3类特征，送入支持向量机，图9给出了两类样本三个特征的三维分布图。随机选取700个作为训练样本，选取合适的参数，得到性能良好的分类器模型。再将剩余300个样本作为测试样本，对识别结果做出预测，对分类器性能进行测试，利用SVM的总分类率为99.5%，植被和建筑物的可分性非常好，支持向量的个数为73个，对存储空间的需求比较小。对整个地区进行识别分类，首先由统计值可设定强度的阈值为65dB，对杂波强度高于阈值提取相应的频谱特征，送入训练好的分类器模型中，可对不同时间段该地区的植被和建筑物的分布情况进行预测分类。

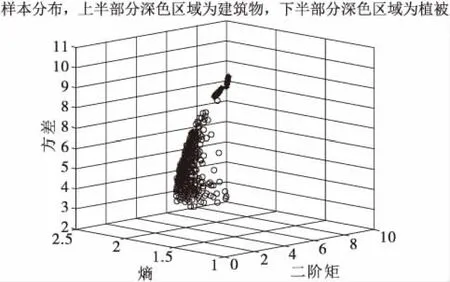
图9 样本分布

4.3 决策融合

对该地区的17次识别结果，进一步采用上述集成学习-多数投票法进行决策融合，即某个距离单元的的决策结果取决于17次分类器输出结果中的大多数。最终的场景分类结果如图10所示，扇形区域内的深色表示建筑物，浅色扇形表示植被，扇形区域外的深色部分表示不进行识别分类。与该地区的Google高清卫星地图进行对比，可较准确的进行场景分类，如图11所示。因此可验证所提方法的有效性。

5 结束语

本文通过提取二阶矩、波形熵、幅度方差3个特征，在有风条件下对某地区的植被和建筑物分布情况进行分类识别，通过对实测数据的分析，表明所提特征是有效的、稳健的。需要指明的是，本方法的适用条件为有风条件下，建筑物多是低矮的农舍，低速目标的出现以及裸土地也会对两类目标的分类有一定的影响，以后会考虑进一步提取新的特征，细化分类结果。

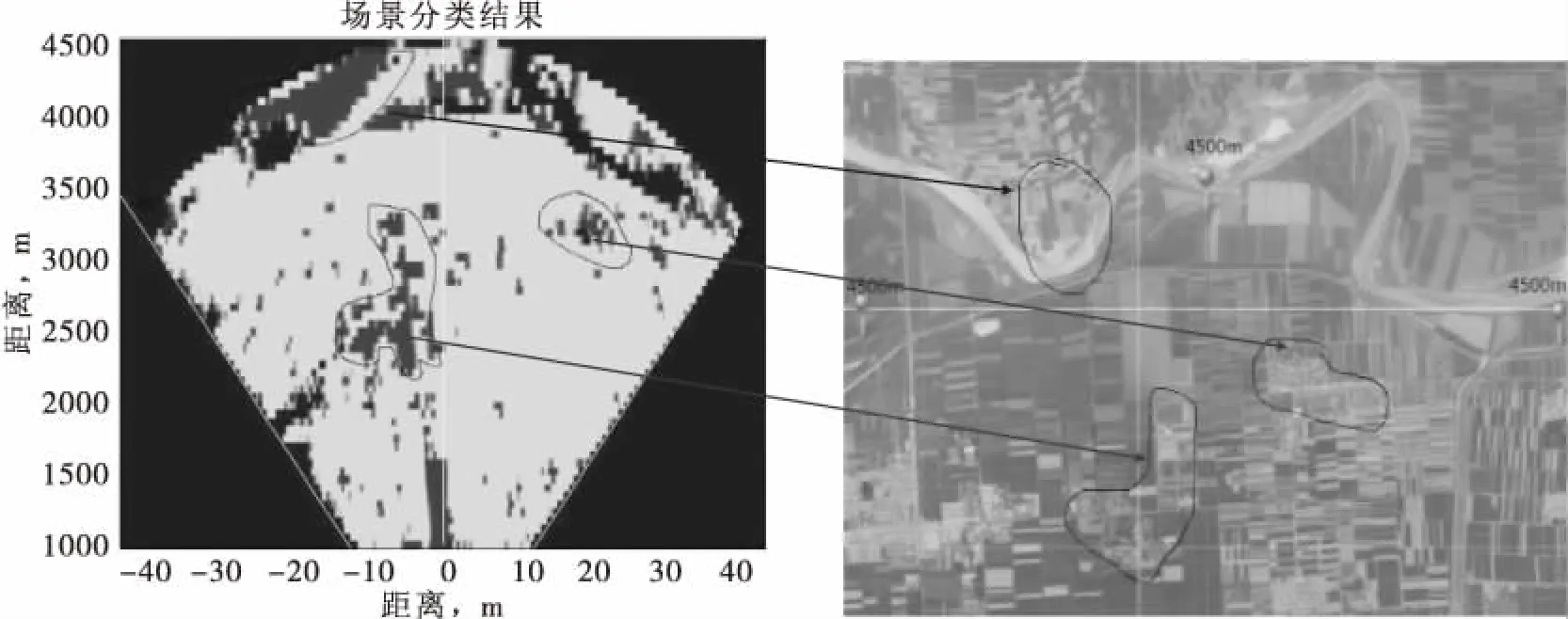
图10 基于二阶矩、熵、方差场景分类结果 图11 地区高清卫星地图