基于随动天线的雷达主瓣干扰抑制

张建明 高才才 王宁可 周书堂

(1.武汉滨湖电子有限责任公司 武汉 430205；2.华讯方舟微电子科技有限公司 广东 深圳 518101；3.中国人民解放军驻三三零三厂军代室 武汉 430200)

0 引言

在我军防空作战装备体系中，侦察预警系统是实施防空作战的重要前提，对防空作战结果具有决定性影响。只有及时发现，准确跟踪来袭目标，为防空作战提供充分的预警时间，才能最大限度地发挥防空武器系统作战效能。但是，随着战场环境日益复杂，自卫式与随队式主瓣干扰、远距离压制式主瓣干扰将在现代战争中扮演越来越重要的角色。传统雷达所具有的副瓣抗干扰技术，如副瓣对消和副瓣匿影等，愈来愈不能满足现代和未来战争的需求[1]，导致现有侦察预警体系的有效作用距离、精度以及预警时间极剧下降。因此，雷达抗主瓣干扰技术的研究迫在眉睫。

现有文献中，已经有学者提出了一些主瓣干扰抑制算法，比如基于下列技术的算法：特征子空间、阻塞矩阵、盲源分离、多子阵或多通道，以及极化等。基于特征子空间的算法[2-4]，一般是基于如下假设的，干扰信号的功率远大于目标回波信号的功率，且干扰信号对应的子空间正交于目标回波信号对应的子空间。基于阻塞矩阵的算法中[5-7]，首先使用阻塞矩阵对接收信号进行预处理，降低干扰信号对协方差矩阵的影响，然后进行自适应波束形成，从而在干扰方向形成凹口。盲源分离最早利用于通信领域，即在缺少源信号和信道参数等先验信息的情况下，将目标信号从观测信号中分离出来。文献[8]中提出使用盲源分离技术来实现干扰信号和目标回波信号的分离。文献[9-11]中提出基于多子阵或多通道的算法，即同时使用来自于多个子阵或多个通道的信号完成主瓣干扰对消。文献[12]提出了基于极化特性的算法，其中，假设发射天线的极化方向是可变的，且假设极化特征是已知或者可测量的。

本文在基于特征子空间算法的基础上，提出一种新的基于随动天线的主瓣干扰抑制技术。该算法的第一步是分别基于主天线和随动天线接收的信号，使用特征子空间算法进行初步干扰对消；第二步是基于最小均方误差估计，将预处理后的随动天线的信号作为参考信号完成二次对消。仿真实验中，比较了本文提出算法和原基于特征子空间算法的性能，结果显示基于随动天线的算法可有效地对抗多个主瓣干扰源。

本文组织结构如下：第一章描述了系统模型；第二章描述了提出的基于随动天线的主瓣干扰抑制算法具体流程；第三章给出了仿真实验结果与分析；最后对全文进行了总结。

1 模型描述

本文提出的算法中，假设雷达站配置了两个天线，即一个主天线和一个随动天线，且两天线相位中心的间距为D；其中，主天线用来发射和接收信号，而随动天线只是单一的接收机。两个天线的指向以及波束指向保持一致。图1给出了目标、干扰以及天线的位置关系示意图。

假设干扰源数目为N，则主天线收到的信号可以用公式(1)表示：

(1)

其中，a1t和a1n分别是目标和第n个干扰相对于主天线，即天线1的导向矢量；τ1t是天线1到目标的双向延时；τ1n是天线1到第n个干扰的延时；S表示主天线的发射信号；Jn表示第n个干扰源的发射信号；n1(t)表示高斯白噪声。类似地，随动天线接收到的信号可以用公式(2)表示：

(2)

且有：

a2t(n)=a1t(n)ej2πD/λ

(3)

其中，λ表示波长。主天线和随动天线均接收到来自于目标的回波以及来自于干扰源的干扰信号。基于随动天线的主瓣干扰抑制问题，即转化为如何利用来自于随动天线的信号r2(t)，抑制主天线接收信号r1(t)中的干扰信号Jn。

图1 目标、干扰以及天线模型示意图

2 干扰抑制算法

2.1 初步对消

干扰抑制算法的第一步是，针对每个天线接收的信号，分别使用基于特征值分解和特征子空间的算法，完成干扰的初步对消。对于每个天线，可以通过公式(4)得到接收信号的协方差矩阵：

R=E[r(t)r(t)H]

(4)

其中，(*)H表示共轭转置。协方差矩阵的特征值分解可以用公式(5)表示：

(5)

其中，M为天线阵元数量，γm和em分别表示特征值及其相应的特征向量。ΛI和EI分别表示干扰信号对应的特征值矩阵和特征向量矩阵，即

ΛI=diag(γ1,γ2,…,γN)

(6)

EI=[e1,e2,…,eN]

(7)

其中，diag{*}表示相应元素构成的对角矩阵。类似地，Λsn和Esn分别表示目标回波以及噪声对应的特征值矩阵和特征向量矩阵。由于不同的信号具有不同的功率，当干扰信号功率远大于目标回波与噪声功率时，特征值满足如下关系：

γ1>…>γN≫γN+1>…>γM

(8)

即，干扰信号对应的特征值远大于目标回波信号或噪声对应的特征值；且可以假设干扰信号对应的特征子空间正交于目标回波信号对应的特征子空间。另外，干扰源的数量N，可以通过经典的最小长度描述算法(Minimum Description Length，MDL)估计。选取EI矩阵的前N-1个向量，构造新的特征向量矩阵：

(9)

(10)

将接收信号投影到干扰信号对应特征子空间，然后减去原接收信号，得到初步对消后的信号：

(11)

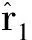
2.2 二次对消

(12)

最小均方误差估计解，表示为：

(13)

(14)

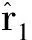
(15)

二次对消的最终结果为：

(16)

3 仿真结果与分析

本章中，我们通过仿真实验，描述了提出的主瓣干扰抑制算法的性能，且将其性能和未使用随动天线的算法进行了对比。

3.1 单个干扰源

假设雷达的工作波长为λ，则天线阵元间的间距为d=λ/2。雷达波束宽度取决于如下公式：

θ3dB=kλ/(dNa)

(17)

其中，k为旁瓣抑制带来的波束展宽系数，一般为1.2～1.4，Na为阵元个数。假设天线在水平向有40个阵元，则阵面法线方向3dB波束宽度为3.7°。主天线和随动天线之间的间隔设置为50m。

仿真实验中，假设主天线和随动天线的坐标分别为(0m，150m)和(0m，-150m)；假设目标和干扰源的位置分别为(150km，150km)和(200km，210km)，即目标和干扰源相对于雷达站的方位角分别为45°和46.4°。方位角的差异为1.4°，即目标和干扰源可能同时落在主天线的主瓣波束内。假设主天线的发射信号为线性调频信号，且带宽为2MHz，脉宽为200μs，脉冲重复频率为2ms，波长为0.2m。信噪比设置为25dB，干噪比设置为60dB，即天线接收到的干扰信号功率比目标回波信号功率高出了35dB。

图2给出了未使用任何干扰抑制措施时的脉冲积累后的距离多普勒图，其中，脉冲积累的数量为32个。显然，目标完全被干扰信号所遮蔽，距离多普勒图上难以发现明显的峰值。图3给出了使用了本文提出的基于随动天线的主瓣干扰抑制算法后的距离多普勒图。图4给出了无干扰、无干扰抑制措施以及使用本文提出的干扰抑制算法后的距离多普勒图的距离切片。可以观察到，当没有使用干扰抑制算法时，距离切片上没有明显的峰值。当进行了主瓣干扰对消后，主瓣干扰得到了有效地抑制，距离切片的旁瓣电平大约是-40dB，即信干比的改善约为40dB。

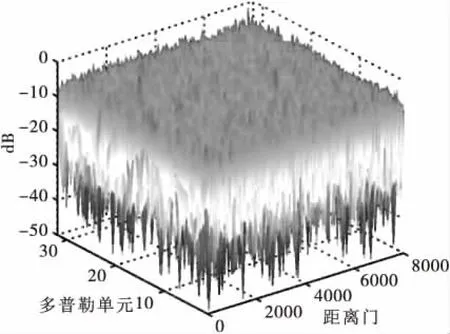
图2 距离多普勒图(未进行干扰抑制)

图3 距离多普勒图(基于随动天线算法)

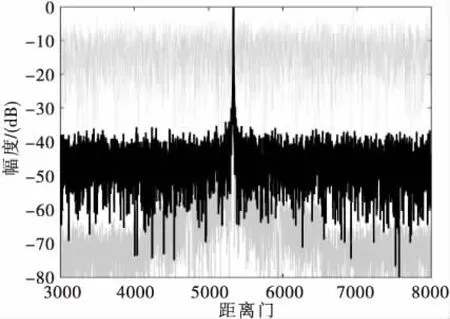
图4 距离多普勒图的距离切片(灰色虚线：未进行干扰抑制措施，灰色实线：无干扰，黑色实线：基于随动天线算法)

3.2 两个干扰源

本节在单一干扰源的基础上，增加另外一个干扰源，且干扰源的位置设置为(200km，187km)，也就是第二个干扰源相对于雷达站的方位角为43°，与目标的方位间隔为2°。另外，该干扰源的干噪比也设置为60dB。

图5给出了使用了本文提出的基于随动天线的主瓣干扰抑制算法后的距离多普勒图。图6给出了使用不同主瓣干扰抑制算法时距离多普勒的距离切片对比，其中，AA代表本文提出的基于随动天线的主瓣干扰抑制算法，ES代表原基于特征子空间的算法。可以观察到，使用基于随动天线算法时，距离切片的旁瓣电平约为-20dB，而未使用随动天线时，距离切片的旁瓣电平高达-5dB，即当主瓣波束内存在两个干扰源时，本文提出算法带来的信干比改善得到了将近15dB的提升。

保持第一个干扰源位置不变，而将第二个干扰源的位置改为(200km，160km)，即其与目标的方位间隔增大到6°，此时，该干扰源不再是从雷达波束主瓣进入，而是从副瓣进入。图7给出了不同目标与干扰源(第二个)方位角间隔下的距离多普勒图的距离切片对比。可见，当方位间隔为6°时，副瓣电平与单干扰源情况下的结果近似；此时，可以认为来自于第二个干扰源的干扰信号被完全对消，即该算法具有较好的副瓣干扰抑制效果。

4 结束语

在本文中，我们提出一种基于随动天线的雷达主瓣干扰抑制算法，将随动天线收到的信号当作参考信号，从而基于特征子空间和最小均方误差估计，抑制从雷达波束主瓣进入的干扰信号。仿真结果显示，当只有一个干扰源，且信噪比和干噪比分别为25dB和60dB时，目标与干扰源的方位间隔为1.4°时，信干比的改善约为40dB。当有主瓣内存在两个干扰源时，相较于未使用随动天线的特征子空间算法，本文提出算法的信干比改善提高了将近15dB。另外，该算法可以起到副瓣匿影的作用，当干扰源不处于主瓣波束内时，干扰源对雷达的干扰基本可以消除。

图5 距离多普勒图(两个干扰源)

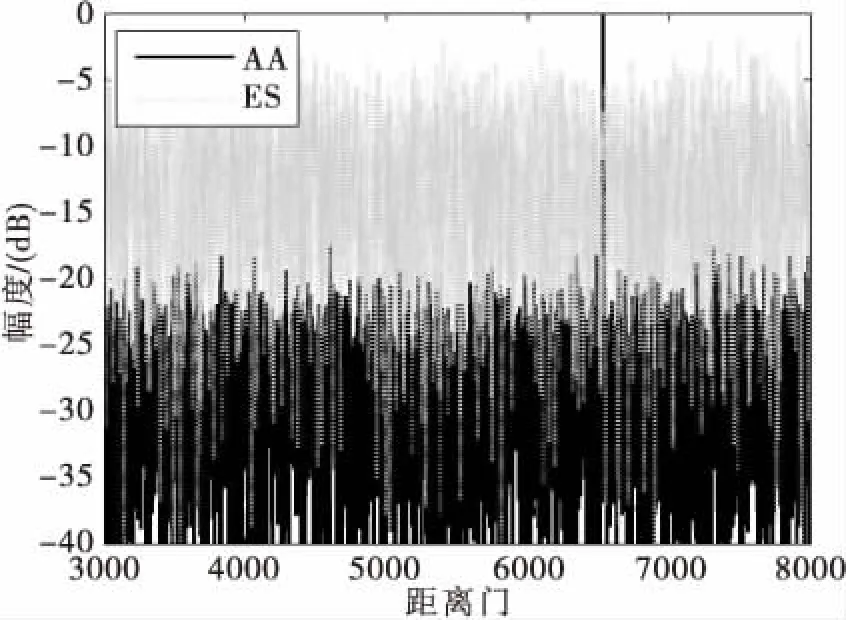
图6 不同主瓣干扰抑制算法的距离多普勒图的距离切片对比(两个干扰源)

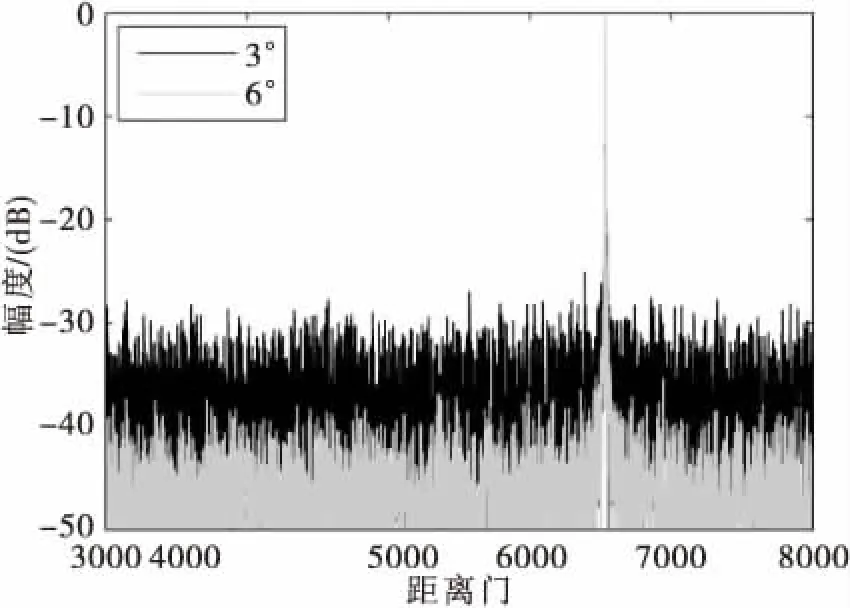
图7 不同目标与干扰源方位角间隔下的距离多普勒图的距离切片对比