多尺度分解结合卷积神经网络的SAR图像识别

高志帮 刘以安

(江南大学 江苏 无锡 214000)

0 引言

合成孔径雷达(synthetic aperture radar，SAR)是一种安装在飞行器上，利用移动的天线在目标区域进行探测的微波遥感成像技术[1]。和传统的基于波束扫描的雷达相比，合成孔径雷达图像分辨率较高，且不受天时，气候和光照的影响。因此SAR图像在资源探测，遥感摄像，军事侦查等领域得到广泛的关注和应用[2-3]。

SAR图像识别的难点在于其成像的机理中，由于其回波信号在不同散射单元强度的随机性，引入了相干斑[4]噪声导致的图像质量的下降。传统的SAR图像识别的过程一般分为三个步骤：图像预处理、特征提取、分类。图像的预处理算法包括Lee滤波，Kuan滤波等，这些方法用来降低相干斑噪声对识别效果的影响，但同时降低了识别的时效性。特征提取方式一般有两种：全局特征提取和局部特征提取。全局特征提取算法包括主成分分析[5](PCA)，独立成分分析(ICA[6])等，这些方法表征了图像的整体信息，但对于图像边缘，纹理等特征表达效果差。局部特征提取方法包括HOG算子[7]，LBP算子[8]，稀疏表示[9]等，描述了图像的局部特征，但没有充分考虑到特征之间的联系性。图像识别方法包括神经网络，SVM[10]，KNN[11]等，得到非常广泛的应用，但是由于SAR图像场景的复杂性，成像机理的特殊性以及对于实时性的要求，增加了识别的难度。

卷积神经网络[12](CNN)是一种前馈人工神经网络，被广泛应用到图像识别的领域。CNN和传统的人工神经网络相比最重要的是卷积和池化的操作。卷积是一种数学运算方式，在卷积神经网络中卷积层利用多个卷积核对图像进行自动特征提取，具有平移不变性，旋转不变性的优点；而池化层则减少了特征的数量，概括了局部特征的特性，减少了参数的数量。池化方法有平均值池化法和最大值池化法。但是卷积神经网络需要海量的数据集作为支持，缺少数据则会导致特征提取能力的不足，这对卷积神经网络的效果产生了影响。

非下采样轮廓波变换(NSCT)[13]是一种多尺度的图像分解方法。经NSCT分解出的高频分量包含了图像的边缘，细节等关键信息，可以增强神经网络特征提取的能力。同时，NSCT在图像分解的过程中取消了下采样的步骤，继承了轮廓波变换(CT)的多方向性和各向异性，还具备轮廓波变换(CT)缺乏的平移不变性，能够有效应对图像的旋转，平移等操作。

提出一种基于NSCT多尺度分解和卷积神经网络(CNN)的合成孔径雷达图像识别方法。首先在使用NSCT对原图像进行尺度分解，并将获取的高低频特征图分量进行空间连结，输入卷积神经网络进行训练和识别。实验结果表明，提出的算法能有效提高神经网络的识别率。

1 基本原理

1.1 非下采样轮廓波变换

非下采样轮廓波变换(NSCT)是一种基于轮廓波变换(CT)的多尺度分解方法。经非下采样轮廓波分解后的高频分量包含边缘细节信息，低频分量包含轮廓、纹理等信息。经NSCT分解后的zoneplate图像如图1所示。

图1 zooneplate原图和NSCT分解结果

NSCT的分解过程主要有两个步骤：第一是非下采样塔型分解(NSP)；第二是非下采样方向滤波组(NSDFB)[14]。首先NSP利用两通道二维滤波组对图像进行多尺度分解，通过对当前组波带利用同一个滤波器进行上采样得到下一组波带(Subband)，同时避免了重新设计滤波器的操作。其带来的冗余度为J+1，J表示分解的级数，而小波变换(NSWT)的冗余度为3J+1，和NSWT相比，冗余度减少了三分之一，提高了效率。

非下采样方向滤波组(NSDFB)继承自方向滤波组(DFB)，主要改进是取消了下采样操作。所以其在图像分解过程中主要是上采样。上采样算法如式(1)所示：

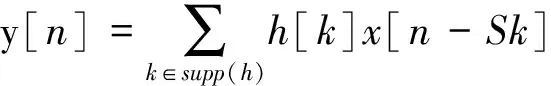
(1)

式(1)中y为输出结果，h是给定的滤波器，Sk为样本矩阵，x为此级波带。从式(1)可以看出，NSCT算法在实现多尺度，多方向性分解的同时，并没有增加计算的复杂度。NSCT算法的分解过程如图2所示。

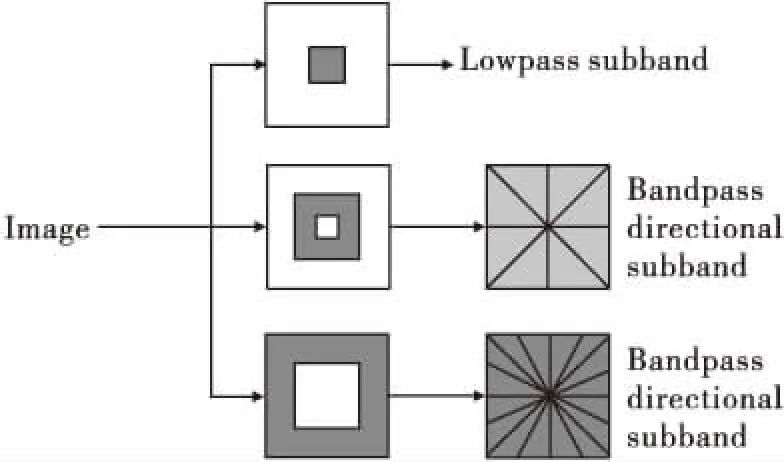
图2 NSCT算法的分解过程

1.2 卷积神经网络算法

卷积神经网络(CNN)是前馈人工神经网络(ANN)的一种改进，通过局部操作对图像特征进行分层抽象，主要被应用在图像领域。LeNet-5[15]是经典的卷积神经网络，包含输入层，卷积层，池化层，全连接层和输出层，其基本结构如图3所示。

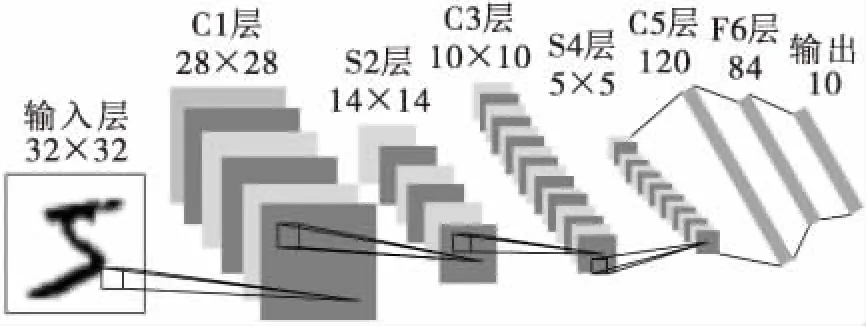
图3 LeNet-5的基本结构

神经网络通过计算损失值并反向传播训练参数。其中二次损失函数定义为：

(2)

其中，x表示输入的样本，y(x)表示实际的值，aL(x)表示预测的输出，L表示神经元的最大层数。代价函数计算输出值和实际值之间的误差，并传递给反向传播函数进行参数更新。

卷积操作能够提取图像的边缘特征，同时对于图像的旋转，平移等变换具有较好的稳定性。为了更充分地提取图像的深层信息，卷积层一般是由多个卷积核组成。卷积核是一个二维矩阵，一般是3×3或5×5的大小，首先赋予卷积核的权值一个初值，由训练决定最终的结果。卷积层的计算公式为：

F=sigmoid[conv(M,N)+B1]

(3)

式(3)中：sigmoid为激活函数；conv为卷积函数；M是输入矩阵，大小为p×p；N为卷积核，大小为q×q；B1为偏置矩阵；F为得到的(p-q+1)×(p-q+1)维特征图矩阵。对同一个图像来说，不同的卷积滤波器运算会产生不同的特征值，因此训练得到合适的卷积滤波器是图像识别成功的关键。

池化操作是图像处理领域经常使用的操作，池化将图像的一个局部内的像素点用一个像素点来代替。池化的作用第一是减小图像的大小和参数的数量，第二是增加算法的稳定性。假设特征矩阵为J，偏置为B2，获得的采样矩特征图为O，则计算方式为：

O=Φ0(J)+B2

(4)

常用的池化操作有平均池化和最大值池化两种。假设特征图为L，池化移动的步长为d，得到的采样结果为S。平均池化和最大值池化计算公式为：

(5)

S=max(Lij)

(6)

式(6)中max函数表示从输入的特征图L中提取最大值。

2 本文算法

图4所示为本文的算法结构图。尺度分解结合卷积神经网络的图像识别主要由三个方面组成：图像预处理，尺度分解进行特征提取，CNN训练分类。图像预处理主要有灰度归一化、尺度归一化、数据增强等。主要目的是节省网络的收敛时间，同时提高样本的数量。经过图像预处理之后，图像的大小为128×128，灰度范围为[0,1]。

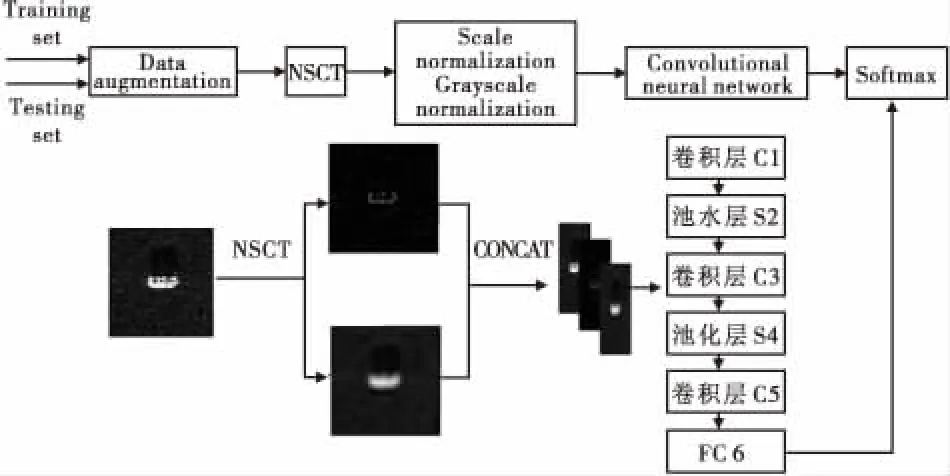
图4 算法结构图

尺度分解算法利用NSCT对原图像进行尺度分解，将分解出的高低频分量与原特征图空间连结，作为新的特征。计算过程如式(7)所示：

H(x)=f(x)⊕Nsct(f(x))h⊕Nsct(f(x))l

(7)

其中f(x)表示输入的特征图，Nsct(f(x))h表示尺度分解f(x)获取高频分量；Nsct(f(x))l表示尺度分解f(x)并获取低频分量；⊕表示空间连结操作。特征提取之后加入到网络进行训练，最后使用softmax分类器对测试集进行分类。

具体的步骤如下：

1)对样本进行数据增强[16](Data Augmentation)。包括对图像进行剪裁、翻转、颜色变换等操作。

2)对从1)获得的数据进行NSCT变换，将原图、高频分量和低频分量空间连结。

3)进行尺度归一化和灰度归一化处理，得到大小为64×64×3，灰度范围在[0,1]之间的数据集。

4)将得到的数据作为神经网络的输入，进行卷积操作和池化操作，得到FC层特征，计算损失值并通过反向传播算法训练网络模型参数。

5)将测试样本输入训练好的网络，通过softmax分类获得预测结果。

3 实验与分析

3.1 实验设置

为了验证算法的有效性，采用MSTAR(Moving and Stationary Target Acquisition and Recogniton)[17]公开数据库作为实验对象。数据库包含了三个场景，八种识别目标。俯仰角度主要有15°和17°。同一场景下的每种目标的图像有299张。将15°和17°的图像作为数据集，以80%的比例作为训练集，20%的比例作为测试集。选取的7种对象作为识别的目标。图5展示了七种目标的光学图像和对应的SAR图像。

图5 七类目标的光学和对应的SAR图像从左到右依次为2S1(榴弹炮)，BRDM2(装甲车)，BTR70(装甲车)，D7(推土机)，T72(坦克)，ZIL131(拖拉机)，ZSU-23(坦克)

实验中使用的卷积神经网络共七层，包含三个卷积层，两个池化层交替连接，最后是全连接层和输出层，激活函数为TANH激活函数。具体参数如表1所示。

表1 卷积神经网络结构图

LayerTypeMapsSizeKernel sizeStrideActivationOutFully Connected-7--RBFF6Fully Connected-84--tanhC5Convolution1201×15×51tanhS4Max Pooling1629×292×22tanhC3Convolution1658×585×51tanhS2Max Pooling662×622×22tanhC1Convolution6124×1245×51tanhlnInput3128×128---

实验模型主要是基于TensorFlow深度学习框架搭建而成，实验硬件环境：Intel(CORE)I5-4200H，8G RAM,NVIDA GeForce GTX TitanX GPU；软件环境：Ubuntu 16.06操作系统，TensorFlow深度学习框架。

3.2 实验结果与分析

如表2所示，是本文算法(NSCT+CNN)与神经网络(CNN)，支持向量机(HOG+SVM)[18]，K最近邻算法(HOG+KNN)的比较结果。每组实验的结果均是取三次实验结果的平均值。其中，卷积神经网络(CNN)使用的是LetNet-5网络结构，激活函数是sigmoid；支持向量机(HOG+SVM)使用的是MATLAB版本的LIBSVM3.22，核函数为高斯核函数；K近邻算法(KNN)选择的K值为10。从表中可以看出NSCT+CNN的识别率最高，达到93.3%，超过CNN算法近4个百分点。而对于SVM和KNN算法，选择了HOG算子作为特征提取算法，其识别率分别为87.6%和73.0%。值得一提的是提出算法的运行时间比CNN长1.3s，主要是因为尺度分解算法需要耗时，但随着计算机计算能力的提升，这个问题的影响会越来越小。

表2 本文算法与其他算法的比较结果

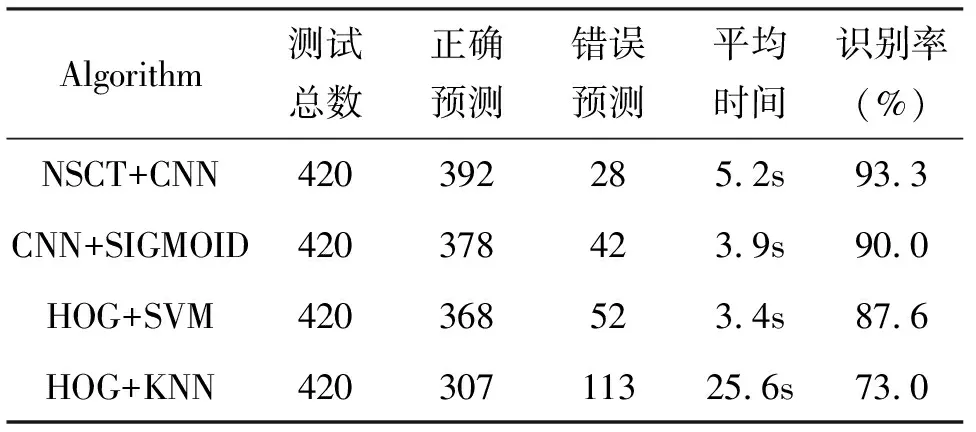
Algorithm测试总数正确预测错误预测平均时间识别率(%)NSCT+CNN420392285.2s93.3CNN+SIGMOID420378423.9s90.0HOG+SVM420368523.4s87.6HOG+KNN42030711325.6s73.0

SAR图像识别的精度受相干斑的影响较大，为了测试算法的鲁棒性，基于实验数据，测试了各组算法在不同级别噪声下的识别率。图6展示了目标2S1经五级椒盐噪声后的图像，其中信噪比分别为0.01，0.02，0.03，0.04，0.05。其识别结果如表3所示。结果表明，本文提出的算法的鲁棒性较高。在五级噪声下，识别率受到较小的影响，下降了0.5个百分点，低于其他几种算法下降的程度。几组实验的结果均验证了本文算法的有效性和可行性。

图6 五级椒盐噪声信噪比依次为0.01、0.02、0.03、0.04、0.05

表3 五级噪声下的识别率比较

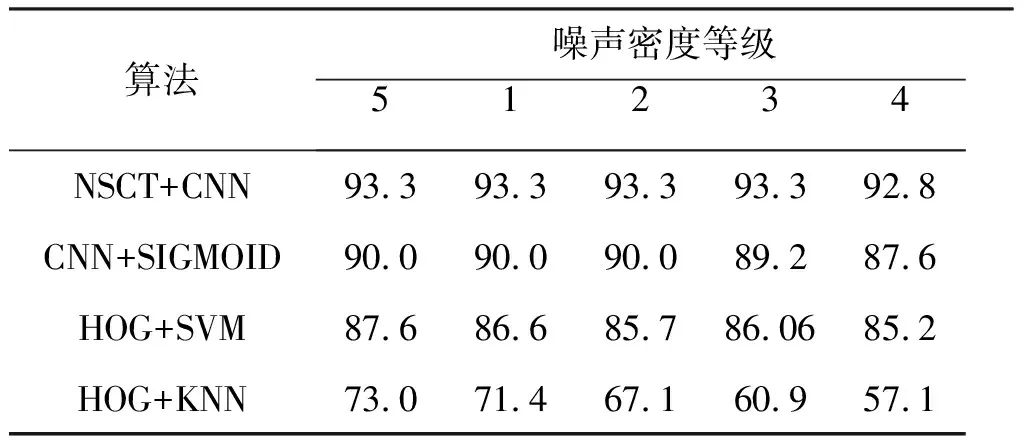
算法噪声密度等级12345NSCT+CNN93.393.393.393.392.8CNN+SIGMOID90.090.090.089.287.6HOG+SVM87.686.685.786.0685.2HOG+KNN73.071.467.160.957.1

4 结束语

本文提出一种基于尺度分解和卷积神经网络的SAR图像识别方法。首先通过非下采样轮廓波变换提取原图像的高低频信息，然后把原图及高低频分量空间连结作为特征图输入网络进行训练。实验结果表明，和几种典型算法相比，提出的算法具有较高的识别率，在MSTAR数据库上达到93.3%；同时，算法具有较高抗噪性，在五级椒盐噪声的影响下下降了5%，能够在一定程度上应对SAR图像识别中的相干斑问题。算法的不足之处是识别速度有待提高，如何进一步提高算法的识别速度是研究的主要方向。