直升机载雷达波束稳定的研究

高一栋 牟 聪 任 强

(西安电子工程研究所 西安 710100)

0 引言

直升机载多功能火控雷达(以下简称机载雷达)区别于常规地面雷达，大部分地面雷达工作时处于非机动状态，其天线坐标系较为固定，而直升机为空中运动平台，飞行机动性强，体积小、重量轻，受地形、气流、风力影响较大，飞行过程中，偏航角、横滚、纵摇三轴姿态极不稳定，另外，由于雷达安装在飞机旋翼顶部，旋翼旋转后导致雷达振动，影响较为强烈，因此机载雷达波束稳定控制相对麻烦[1]。

在实际飞行中，飞机的姿态变化是非常剧烈的，对波束稳定的影响同样是巨大的。因此，需要对波束进行补偿，无论飞机姿态发生任何变化，都要保持波束在空间中的位置不变。在飞机的操控终端上，操作指令是按照大地坐标系下发送工作指令，雷达天线的方位、俯仰位则是在天线坐标系中进行的控制，因此，需要结合当前的飞行姿态角，根据当前的操作指令，将大地坐标系下的角度变换到天线坐标系的角度。上报角度数据时，伺服发送的是天线坐标系下的角度数据，因此，还需要将该数据进行坐标反变换，转化为大地坐标系下的角度发送给操控终端。部分文献给出了坐标的转换方法，适用于大部分常规的机械扫描雷达[2-4]。

本系统对地模式为相扫，对空则使用机械圆周扫描方式，相扫模式下坐标转换相对复杂，而机械扫描方式坐标转换相对简单，因为机械扫描时载机坐标系与天线坐标系重合，而相扫时，天线坐标系与载机坐标系不同。因篇幅所限，本文重点对相扫时坐标转换公式进行详细的推导,而对机械扫描方式坐标转换给以简单说明。

1 多种因素导致波束稳定

导致波束稳定的因素角多，雷达安装误差、校靶、惯导校准不精确，都会导致无法得到精确角度。由于采用一维相扫，天线坐标系与传统机械扫描坐标系具有一定的差异，表现在较大的方位扫描角度时，俯仰下降，在地形探测时表现尤为突出。对于雷达安装标校属于测量的范畴，这里不再赘述，本文重点对旋翼振动、飞行姿态变化、坐标系的差异三个方面进行论述。

1.1 飞行姿态的影响

图1为雷达波束照射示意图，以此举例说明，当直升机处于飞行状态时，由于雷达安装在直升机顶部位置，因此，雷达与直升机机体同步摆动，当飞机姿态发生变化时，雷达波束位置也将随着机体姿态发生变化，也就意味着，雷达坐标系与机体坐标系是相同的,雷达坐标系与大地坐标系不一致，在图1(a)可看到，飞机处于平稳状态，雷达与固定翼飞机保持在同一水平面，也就是说在空间大地坐标系下，对于雷达而言，固定翼飞机处于俯仰0°位置，此时直升机为水平姿态，因此0°波束俯仰位可以发现该固定翼飞机；在图1(b)中，机头向下倾斜，飞机纵摇发生了变化，纵摇角为负，因此雷达波束照射到固定翼飞机下方位置，同样，在图1(c)中，机头向上倾斜，纵摇角为正值，波束照射到飞机上方位置，同样导致目标丢失。

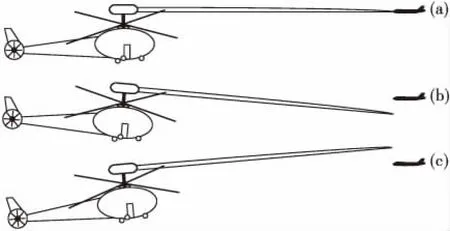
图1 载机带来波束抖动示意图

1.2 雷达天线坐标系与载机坐标系的差异

天线坐标系与载机坐标系的差异，是针对方位相扫时而言，而机械扫描则不存在上述问题，图2是标准坐标系图，为机械扫描时空间波束，图3为相扫时空间波束，两幅图中，OX代表飞机纵轴方向，与天线法线重合，在雷达安装时，需要进行标校，与飞机轴线进行重合。OY轴为垂直向上，OZ轴则按右手定则进行确定，下面分析机械扫描与相扫时天线坐标系的区别：

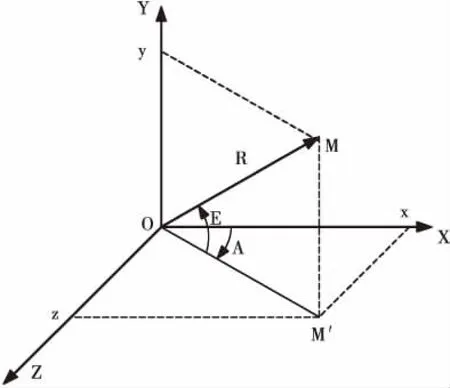
图2 机械扫描坐标

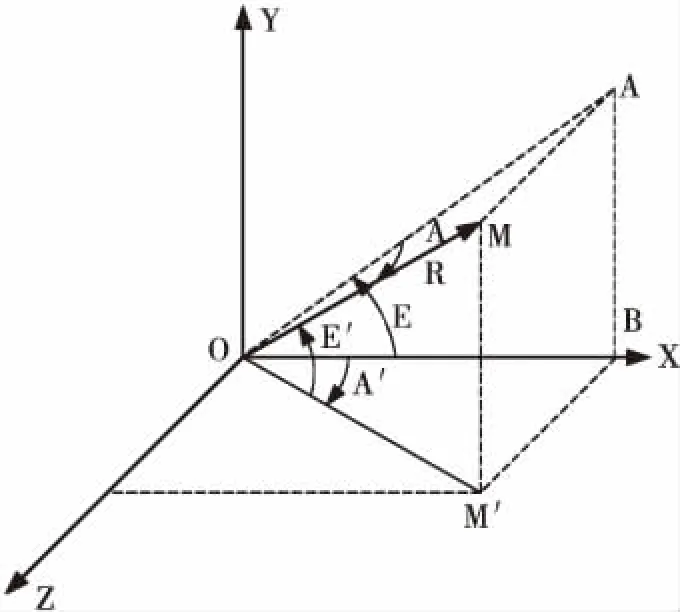
图3 相扫坐标

在图2中，波束方位为A ，俯仰为E，可以得出：

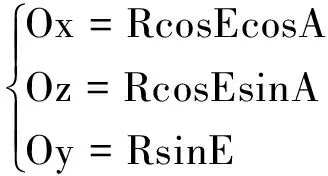
(1)

以图3为例说明，与图2不同的是，波束在MOA所示的平面内进行相位扫描，方面扫描0°，天线俯仰角度为E，当扫描到M点位置时，俯仰角度为E′，可以看出， E> E′，也就意味着，伺服设定某个固定俯仰角度，方位角进行扫描，在法线位置处，俯仰角最大，随着方位远离法线方向，俯仰减小，俯仰呈下降趋势。在极限情况，假如方位能够扫描到90°，则俯仰位变为0°。可总结如下公式：

(2)

实际空间方位、俯仰角为：

(3)

图4 俯仰波束覆盖示意图

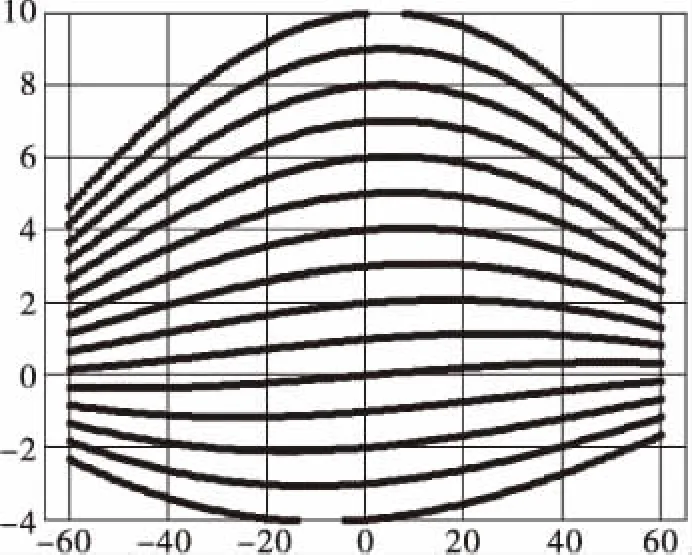
图5 俯仰波束畸变示意图

从公式(3)可以看出，在俯仰较小时，方位角度差别很小；在方位较小时，俯仰角度差别很小。实际工程运用中，在雷达对地、对空、高压线探测模式中，不需要扫描较大的空域范围，俯仰波位少，仅扫描一到两行，而且俯仰波位较低，一般扫描0°及以下角度即可，因此，两者俯仰位差别较小，因而可以忽略不计。需要对地形探测时，方位覆盖从-45°到45°或者-60°到60°俯仰位则需要安排较多的俯仰波位，为探测出山形地貌，安排了数十个俯仰波位，图4中，地形探测模式覆盖了方位从-60°到60°，俯仰从底部-4°到上端10°的区域，可以扫描大部分山形区间，实际根据山形实际高度进行调整。由于方位采用相扫，俯仰采用了机械扫描，实际上的波束空间分布随着方位增大，俯仰下降，从图5中可以统计出，在方位扫描到60°处，本在10°处的俯仰波位，实际空间位置下降到5.3°左右，因此将导致严重后果：第一，地形探测时将遗漏空域，当俯仰位处于高波位时，下降趋势将变得更加严重，方位波束无法照射到两侧的较高的山脉；第二，由于使用了非准确的俯仰位，导致山形产生畸变，雷达界面的山脉轮廓与实际山形不一致。因此需要对俯仰波束进行实时补偿，在俯仰为正值，方位扫描时，逐步抬高两侧俯仰波束，反之，俯仰下视时，随着方位扫描，两侧俯仰波束降低，实际空间波位覆盖时，以尽可能接近图4所示的理想状态。

1.3 旋翼振动

由于雷达是安装在直升机旋翼的上方，因此旋翼旋转时对俯仰波束位置影响是巨大的，图6选取某次飞行较为平稳的俯仰统计图，横坐标为CPI计数，纵坐标为角度值，o曲线代表俯仰码盘值，可以看出，由于振动原因，该曲线抖动较大，经统计，俯仰波位有±0.7°的抖动，振幅达1.4°很容易导致丢失目标。尤其是在高压线探测模式，丢失任何一组目标信息将使高压线规律性变差，以致无法区分地面静目标与高压线，最终导致无法连线，也就是说雷达并未检测到高压线。这无疑对雷达探测影响是巨大的，因此需要采取其它措施以减小波束抖动。

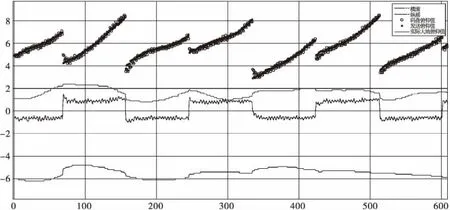
图6 旋翼振动示意图

2 坐标系转换

2.1 雷达相扫坐标转换[5]

1)地理极坐标系到地理直角坐标系的转换

极坐标系转换到直角坐标系示意图如图2所示，极坐标转换成直角坐标公式见式(1)。

2)地理直角坐标系到载机直角坐标系的转换

该转换涉及到偏航、横滚、纵摇三轴转换，在推导变换公式时，首先只考虑一种姿态的变化，另外两种姿态保持不变，先分后合，分别推导出公式后，再将各姿态同时变化时态综合考虑，进行叠加相乘。

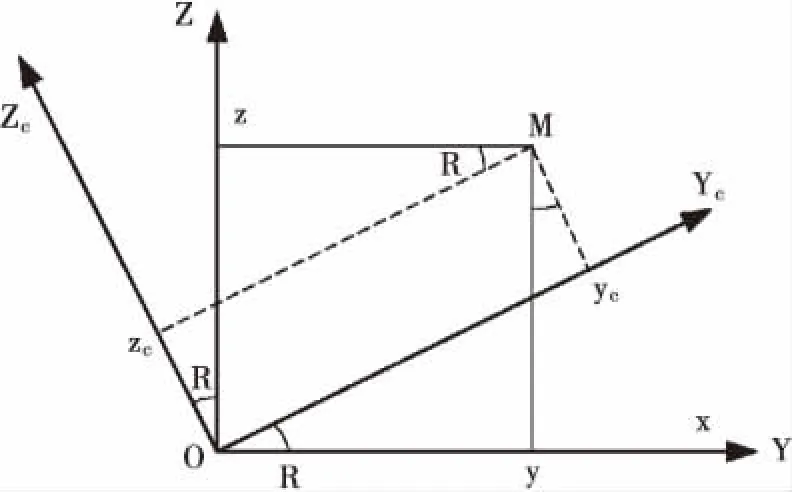
图7 仅考虑横滚角变化时的坐标转换

①横滚角R发生改变时，以上图所示，可认为是Y轴与Z轴绕X轴旋转，Y轴和Z轴转过的角度为R。设空间某点M在大地坐标系中为M(X,Y,Z)在载机直角坐标系中为MC(XC,YC,ZC)，见图7。

Oyc=ON+Nyc

=Oy/cosR+(My-Ny)sinR

=Y/cosR+(Z-YtgR)sinR

=Y/cosR+ZsinR-sin2R·Y/cosR

(4)

Ozc=Myc=MNcosR=(Z-sinR·Y/cosR)

=-YsinR+ZcosR

(5)

用矩阵形式表示为：

②同理，仅纵摇角P发生变化时，可以认为绕X轴与Y轴绕Z轴旋转，X 轴和Y轴转过的角度为P。把Y →X；Z →Y； R → P； YC → XC ； ZC → YC。

同理可推出：

Oxc=XcosP+YsinP

(6)

Oyc=-XsinP+YcosP

(7)

用矩阵表示为

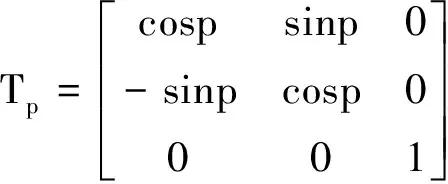
③最后，仅当航当角H发生变化时，X轴与Z轴绕Y轴旋转，X轴和Z轴转过的角度为H，则有

Oxc=ON+Nxc
=X/cos H+(Z-sin H/cos H)sinH
=Xcos H+Zsin H

(8)

Ozc=xcM=MNcos H
=(Z-sin H·X/cos H)cos H
=-Xsin H+Zcos H

(9)

用矩阵表示为

④综合上述推导的公式，当横摇、纵摇和航向角同时发生变化时

(10)

其中：

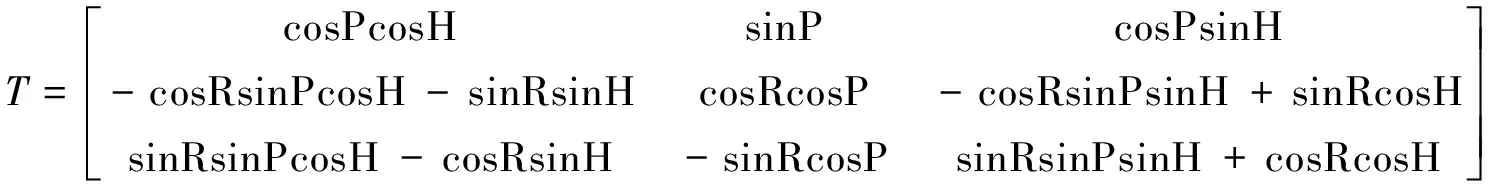
3)地理极坐标到载机直角坐标的转换

(11)

4)载机直角坐标系到载机天线极坐标系转换

天线直角坐标与天线极坐标之间的关系见图4所示。对式(2)做逆变换：

Ac=sin-1(ZC)

(12)

Ec=tg-1(YC/XC)

(13)

需要注意的是，当方位电轴为0°，也就是与载机纵轴线重合时，可以使用以上述坐标转换方法。

当雷达方位转台转动时，坐标转换更加复杂，使用公式(1)时，方位值使用相扫方位值加上电轴转台码盘值，在第3与第4步转换之前，需要做一次电轴坐标转换，下面给出公式。

XC′=cos(AXIS)·XC+sin(AXIS)·ZC

(14)

YC′=YC

(15)

ZC′=(-1)·sin(AXIS)·XC+cos(AXIS)·ZC

(16)

2.2 雷达机械扫描坐标转换

方位机械扫描坐标系转换与方位相扫坐标系转换相似，主要区别在于载机天线极坐标系到载机直角坐标系的变换。

对图1的变换公式(1)做其逆变换即可：

Ac=tg-1(ZC/XC)

(17)

Ec=sin-1(YC)

(18)

3 飞行试验效果分析

图8为机载雷达某次对地飞行实验时的俯仰波位统计图，图中，“o”表示俯仰回报的码盘值，原点“.”表示的是向伺服系统发送的俯仰角，“-.”曲线为载机的横滚角，“--”为载机的纵摇角度，最后实线条“-”表示为俯仰空间实际的指向值。

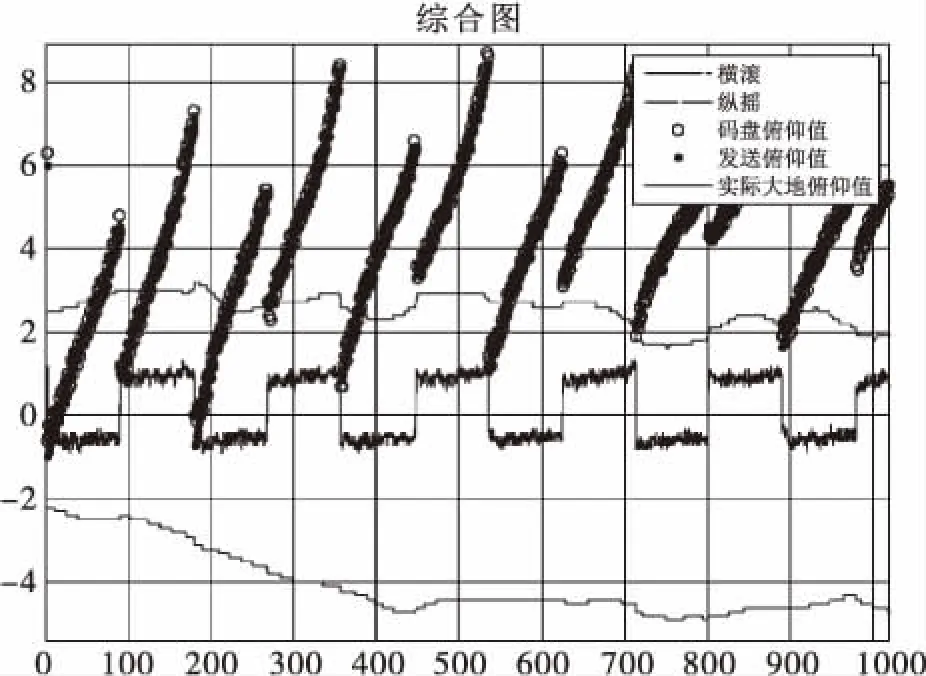
图8 相扫时俯仰波束补偿效果图

统计实际俯仰角度，容易看出，实线条所代表空间俯仰值，在一个小的范围内进行步进角扫描，步进角度为1°，与操控终端设定俯仰波位大体一致，说明空间波束补偿到位，其上下抖动是旋翼振动带来的，无法避免，整体补偿效果理想。

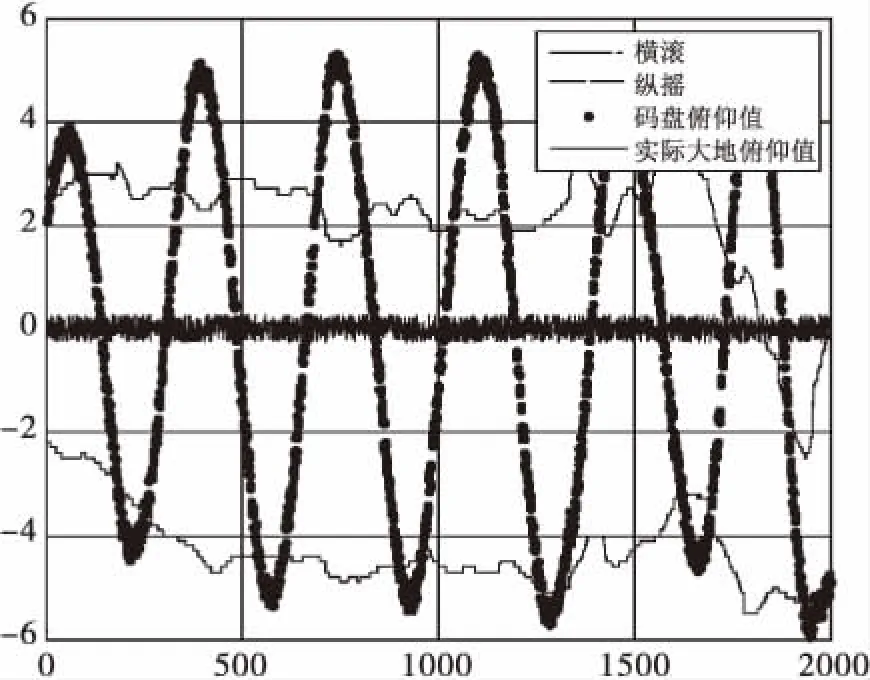
图9 机械扫描俯仰波束补偿效果图

图9为机载雷达在对空模式试验时的俯仰波位统计图，上图中，以“.”连接的曲线为俯仰码盘值，“-.”曲线为载机的横滚角，“--”为载机的纵摇角度，实线条“-”表示为俯仰空间实际的指向值。

可以看出，在载机极坐标系下，俯仰为正弦式扫描，统计实线条“-”线条，发现其值代表空间俯仰值，在0°的范围内抖动，为固定角俯仰角，与操控终端设定的俯仰波位吻合，意味着波束补偿基本到位。但是通过放大显示，发送的俯仰波位与回报的码盘值略有所差异，经过数学分析，实际统计俯仰码盘均值大于理论计算值0.2°左右，通过修正伺服俯仰指令值，消除该差异。

4 优化事项

1)应用公式时，需要注意， 在求方位角时，要用到反正切函数，这就有一个象限确定的问题。

2)由于伺服系统响应的滞后性，因此，波束稳定对于伺服控制需要有一个时间提前量，对于不同工作模式，对应的prf不同，造成工作周期不同，该时间提前量也不尽相同，并且不同批次的伺服系统，性能也有所差异，因此需要每一套伺服进行测试。

3)雷达在地面静止时，可选取具有代表性的飞机数据，进行模拟波束补偿，通过数采设备以及matlab软件，精心测试，测试出控制时间的最佳调整值，以达到最佳补偿效果。

5 结束语

上述分析表明，直升机载雷达的波束稳定，可通过任务计算机(中心机)，实时进行坐标转换，将计算的波束补偿角，再发送给伺服系统，实现波束补偿。在实际飞行试验过程中，进行了精度测试项目，包含距离、角度、速度精度测试，在配试目标与载机加装了差分GPS系统，以两套GPS直接的距离、角度为真值，来验证雷达的性能，数采设备对飞行数据实时记录，通过中心机对录取的飞行数据进行分析，实际空间指向角与通过GPS统计的出角度值较为吻合，满足精度了测试要求，也间接的证明了直升机载雷达波束稳定方法的正确性。